排序算法 - 快速排序（4种方法实现）

快速排序

• 快速排序是啥？
• 三数取中：
• 1.挖坑法（推荐掌握）
• 2.前后指针法（推荐掌握）
• 3.左右指针法（霍尔版本）（容易出错）
• 4.非递归实现

  本篇文章的源代码在这，需要自取：Gitee

  快速排序是啥？

  快速排序是一种常见的排序算法，其基本原理是分治和递归。它的基本思路是，在数组中选择一个元素作为基准值，然后将数组中小于基准值的元素移动到它的左边，大于基准值的元素移动到它的右边。然后对左右两个子数组递归地重复这个过程，直到子数组的大小为1或0。

  在实现快速排序时，可以使用 三数取中法来选取基准值和分区，这样可以有效避免最坏情况的发生。

  三数取中法：从待排序区间的首、中、尾三个位置上的数选取一个中间值作为基准值。

  三数取中：

  //三数取中
  int GetMidIndex(int* a, int left, int right)
  {
  	int mid = (left + right) / 2;
  	if (a[left]  a[mid]
  	{
  		if (a[mid] > a[right])
  		{
  			return mid;
  		}
  		else if(a[left] > a[right])
  		{
  			return right;
  		}
  		else
  		{
  			return left;
  		}
  	}
  }
  

  1. GetMidIndex 函数接受一个整型数组 a，以及要选择基准元素的左右边界索引 left 和 right。函数首先计算出中间索引 mid，通过 (left + right) / 2 的方式获得。

  2. 然后，函数根据数组中三个元素 a[left]、a[mid] 和 a[right] 的值进行比较，以确定基准元素的索引。

  3. 如果 a[left] 小于 a[mid]，则继续比较 a[mid] 和 a[right]。如果 a[mid] 小于 a[right]，说明 a[mid] 是中间的元素，其值介于 a[left] 和 a[right] 之间，因此将 mid 作为基准元素的索引返回。

  4. 如果 a[mid] 不小于 a[right]，则根据 a[left] 和 a[right] 的大小关系来选择基准元素的索引。如果 a[left] 小于 a[right]，说明 a[left] 是中间的元素，其值介于 a[mid] 和 a[right] 之间，因此将 right 作为基准元素的索引返回。否则，如果 a[left] 大于等于 a[right]，说明 a[right] 是中间的元素，其值介于 a[left] 和 a[mid] 之间，因此将 left 作为基准元素的索引返回。

  5. 如果 a[left] 大于 a[mid]，则继续比较 a[mid] 和 a[right]。如果 a[mid] 大于 a[right]，说明 a[mid] 是中间的元素，其值介于 a[left] 和 a[right] 之间，因此将 mid 作为基准元素的索引返回。

  6. 如果 a[mid] 不大于 a[right]，则根据 a[left] 和 a[right] 的大小关系来选择基准元素的索引。如果 a[left] 大于 a[right]，说明 a[left] 是中间的元素，其值介于 a[right] 和 a[mid] 之间，因此将 right 作为基准元素的索引返回。否则，如果 a[left] 小于等于 a[right]，说明 a[left] 是中间的元素，其值介于 a[mid] 和 a[right] 之间，因此将 left 作为基准元素的索引返回。

  通过使用三数取中法选择基准元素，可以在大多数情况下选取到接近中间值的元素，提高快速排序的效率和性能，并减少最坏情况的发生

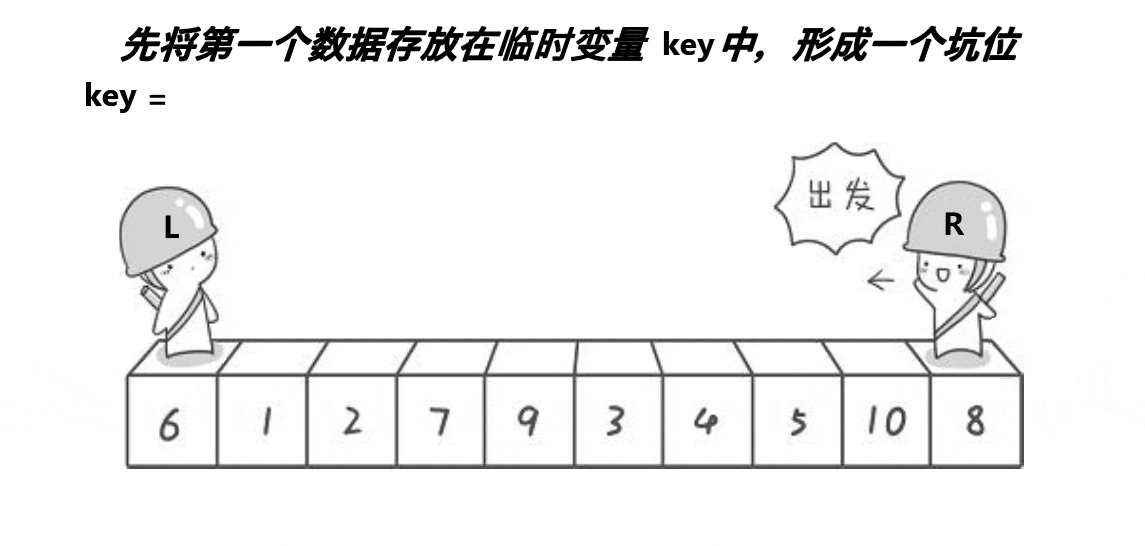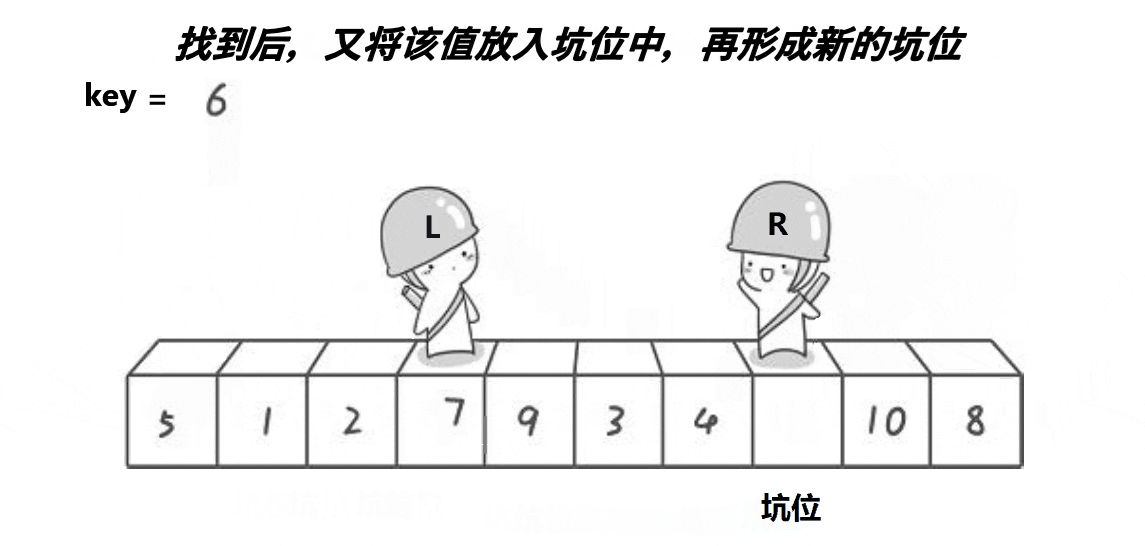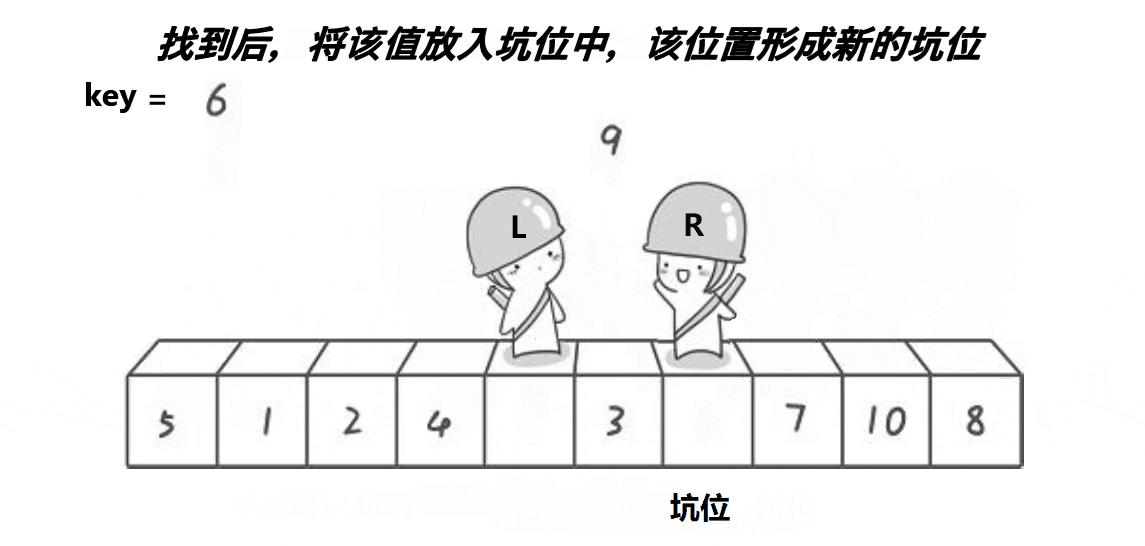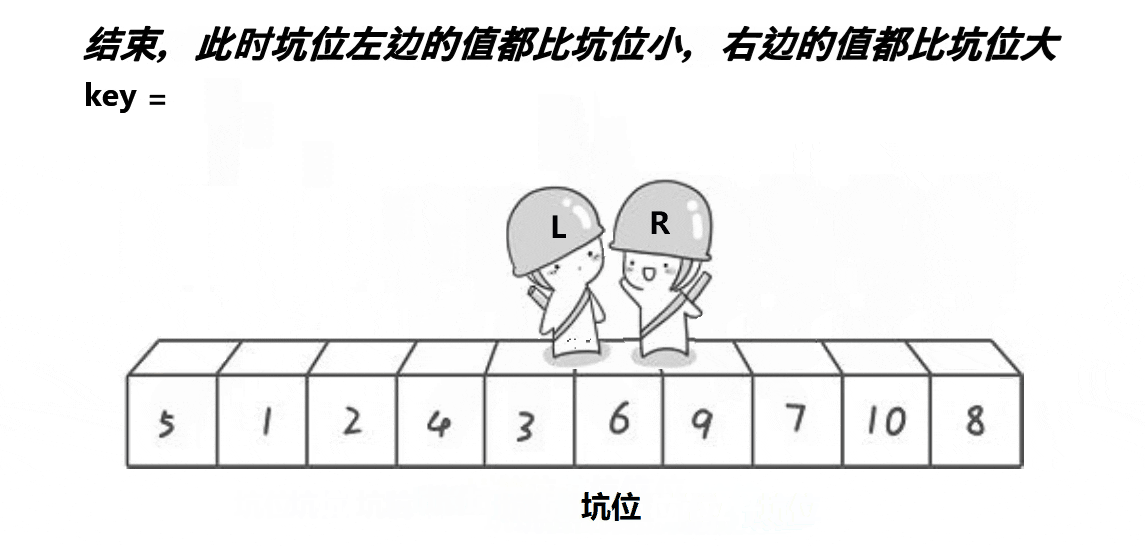
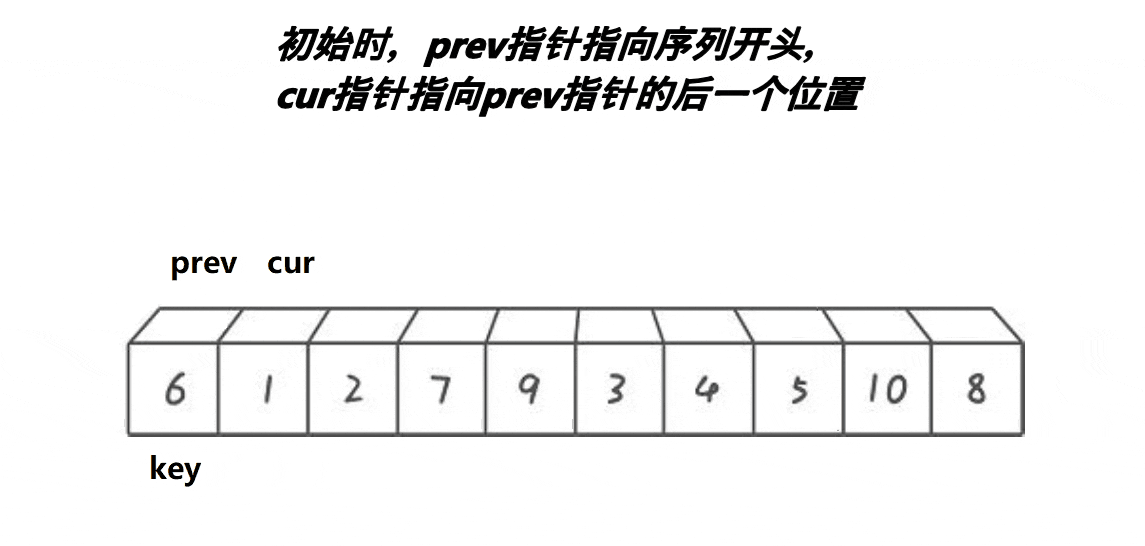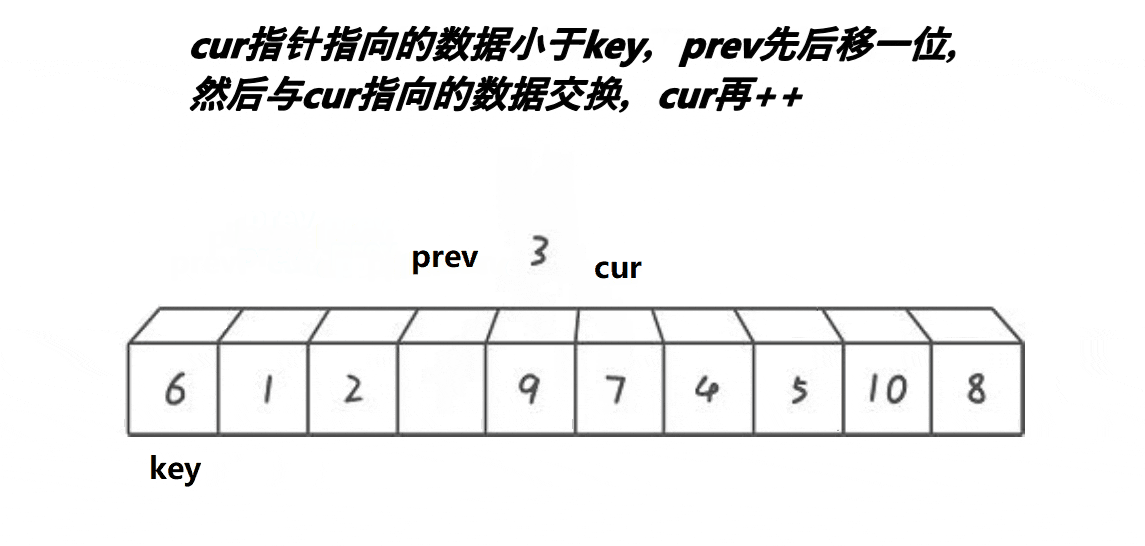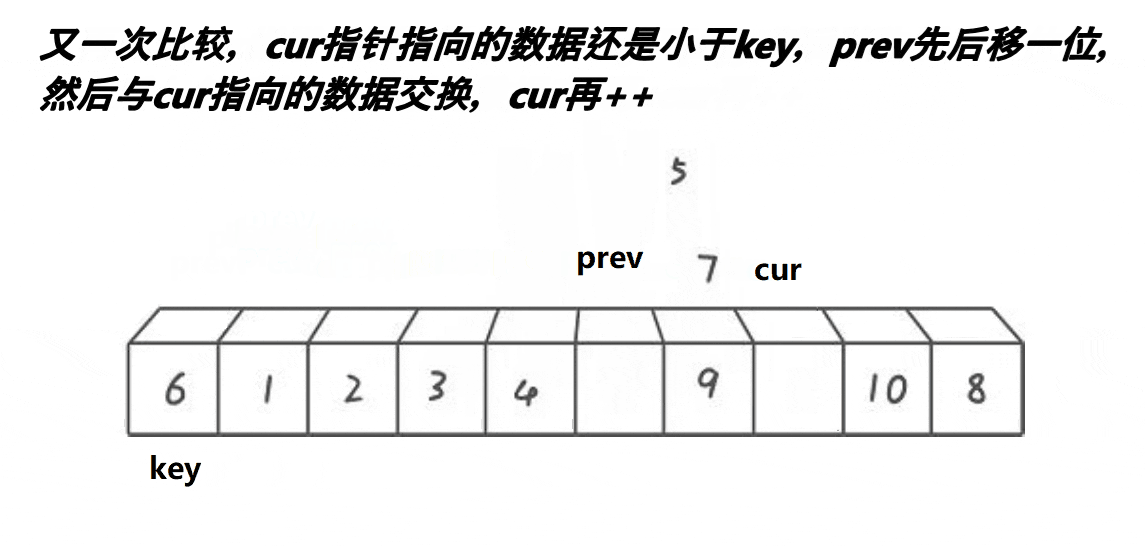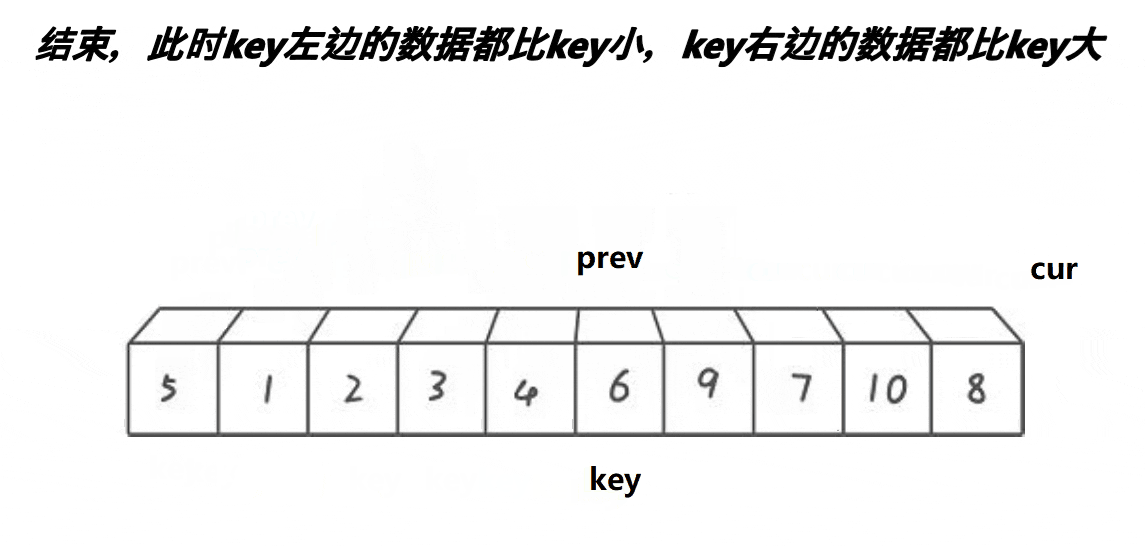
  1.挖坑法（推荐掌握）

  以下是挖坑法的详细过程：

  1. 选择一个值基准值（在这用三数取中）。通常情况下，选择数组中第一个元素作为基准值。
  2. 将数组中小于基准值的元素移动到它的左边，大于基准值的元素移动到它的右边。（左边找大，右边找小）。
  3. 对左右两个子数组递归地重复上述过程，直到子数组的大小为1或0。
  4. 合并子数组，得到排序后的数组。

  

  //挖坑法
  int PartSort2(int* a, int left, int right)
  {
  	//三数取中
  	int midi = GetMidIndex(a, left, right);
  	Swap(&a[midi], &a[left]);//把中间值放到left位置
  	
  	int keyi = left;
  	while (left = a[keyi])
  		{
  			right--;
  		}
  		Swap(&a[keyi], &a[right]);
  		keyi = right;
  		while (left  
   
   
  PartSort2 函数是挖坑法的核心实现。它接受一个整型数组 a，以及要排序的左右边界索引 left 和 right。函数首先选择一个中间索引 midi，并将 a[midi] 与 a[left] 进行交换，将 a[left] 作为基准元素。
  然后，函数使用两个指针 left 和 right 在数组中进行扫描。从右边开始，当 a[right] 大于等于基准元素 a[keyi] 时，将 right 指针左移，直到找到小于基准元素的元素为止。
  然后，将该元素与 a[keyi] 进行交换，将 keyi 更新为 right。
  接下来，从左边开始，当 a[left] 小于等于基准元素 a[keyi] 时，将 left 指针右移，直到找到大于基准元素的元素为止。
  然后，将该元素与 a[keyi] 进行交换，将 keyi 更新为 left。
  重复这个过程直到 left 和 right 指针相遇，然后返回 keyi，该索引将数组分为两部分：左边的元素小于等于基准元素，右边的元素大于等于基准元素。
  QuickSort 函数接受一个整型数组 a，以及要排序的左右边界索引 left 和 right。首先，它检查是否满足递归终止条件，即 left >= right，如果满足条件，则直接返回。否则，它调用PartSort2 函数获取基准元素的索引 keyi，然后将数组分为三部分：[left, keyi-1]、[keyi] 和 [keyi+1, right]。接着，它递归调用 QuickSort 函数对左边和右边的子数组进行排序。
   
   
  2.前后指针法（推荐掌握）
   
   
  //前后指针法
  int PartSort3(int* a, int left, int right)
  {
  	int midi = GetMidIndex(a, left, right);
  	Swap(&a[midi], &a[left]);
  	//end找小，如果	a[end]
  	int keyi = left;
  	int begin = left;
  	int end = left+1;
  	while (end 
  		if (a[end]  
   
   
  PartSort3 函数使用了前后指针法（双指针法）进行数组分区。函数接受一个整型数组 a，以及要分区的左右边界索引 left 和 right。
  首先，函数调用 GetMidIndex 函数获取基准元素的索引 midi，然后将 a[midi] 和 a[left] 进行交换，将 a[left] 设置为基准元素。
  接下来，函数初始化两个指针 begin 和 end，分别从 left 和 left + 1 开始遍历数组。
  在遍历过程中，end 指针向右移动，扫描数组元素。当 a[end] 小于基准元素 a[keyi] 时，将 begin 指针右移一位，并交换 a[begin] 和 a[end] 的值。这样，较小的元素就会被移动到 begin 的位置，而 begin 之前的元素都小于基准元素。
  最后，将基准元素 a[keyi] 移动到合适的位置，即将其与 a[begin] 交换。此时，数组被分为两部分：左边的元素小于基准元素，右边的元素大于等于基准元素。
  最后，函数返回基准元素的索引 begin。
  QuickSort函数作用同上
   
   
  3.左右指针法（霍尔版本）（容易出错）
   
   
   
  快速排序的左右指针法（双指针法）是一种常见的实现方式，它利用两个指针从数组的两端开始，逐步向中间移动，并进行元素的比较和交换，以实现数组的分区和排序。
   
   
  其基本思想如下：
   
  

  • 选择一个基准元素（通常是数组的第一个元素）。

  • 使用两个指针，一个从左边开始（一般称为左指针），一个从右边开始（一般称为右指针）。

  • 左指针从左边开始向右移动，直到找到一个大于基准元素的元素。

  • 右指针从右边开始向左移动，直到找到一个小于基准元素的元素。

  • 如果左指针的位置小于右指针的位置，则交换左指针和右指针所指向的元素。

  • 重复步骤 3-5，直到左指针和右指针相遇。

  • 将基准元素与左指针所指向的元素进行交换，此时基准元素的位置已经确定。

  • 根据基准元素的位置，将数组分成两部分，左边的元素都小于基准元素，右边的元素都大于基准元素。

  • 对基准元素左右两部分的子数组分别重复以上步骤，直到所有的子数组都有序。

    //左右指针（霍尔版本）（容易出错）
    int PartSort1(int* a, int left,int right)
    {
    	int midi = GetMidIndex(a, left, right);
    	Swap(&a[midi], &a[left]);
    	int keyi = left;
    	while (left = right)
    		{
    			return ;
    		}
    		int keyi = PartSort1(a, left, right);
    		//[left,keyi-1][keyi][keyi+1,right]
    		QuickSort(a, left, keyi - 1);
    		QuickSort(a, keyi + 1, right);
    	}
    

    1. PartSort1 函数使用左右指针法（霍尔版本）进行数组分区。函数接受一个整型数组 a，以及要分区的左右边界索引 left 和 right。
    2. 首先，函数调用 GetMidIndex 函数获取基准元素的索引 midi，然后将 a[midi] 和 a[left] 进行交换，将 a[left] 设置为基准元素。
    3. 接下来，函数使用两个指针 left 和 right 分别从数组的左右两端开始遍历。
    4. 在遍历过程中，首先从右边开始，找到第一个小于基准元素的元素，将 right 指针左移一位，直到找到小于基准元素的元素或 left 和 right 指针相遇。
    5. 然后，从左边开始，找到第一个大于基准元素的元素，将 left 指针右移一位，直到找到大于基准元素的元素或 left 和 right 指针相遇。
    6. 如果 left 小于 right，则交换 a[left] 和 a[right]，将小于基准元素的元素移动到左侧，大于基准元素的元素移动到右侧。
    7. 重复上述步骤，直到 left 和 right 指针相遇，此时完成了一次分区。将基准元素 a[keyi] 移动到合适的位置，即将其与 a[left] 交换。
    8. 最后，函数返回基准元素的索引 left。

    QuickSort函数同上

    4.非递归实现

    • 非递归的快速排序使用栈来存储待处理的子数组的起始和结束位置。初始时，将整个数组的起始和结束位置压入栈中。

    • 然后，进入循环，从栈中弹出一个子数组，对其进行分区操作，得到基准元素的位置。根据分区的结果，将子数组划分为两个部分：一个部分是基准元素左边的子数组，另一个部分是基准元素右边的子数组。

    • 接下来，将需要进一步处理的子数组的起始和结束位置压入栈中。这样，栈中存储的就是待处理的子数组。

    • 重复以上步骤，直到栈为空。这意味着所有的子数组都已经被处理完毕，排序完成。

    • 通过使用栈来模拟递归调用过程，非递归的快速排序能够有效地对数组进行分区和排序，同时避免了递归带来的函数调用开销。这种实现方式通常具有较好的性能和效率，特别适用于处理大规模的数据集。

      void QuickSortNonR(int* a, int begin, int end)
      {
      	ST st;
      	StackInit(&st);
      	StackPush(&st, end);
      	StackPush(&st,begin);
      	
      	while (!StackEmpty(&st))
      	{
      		int left = StackTop(&st);
      		StackPop(&st);
      		int right = StackTop(&st);
      		StackPop(&st);
      		int keyi = PartSort2(a, left, right);
      		//[left,keyi-1][keyi][keyi+1,right]
      		if(keyi+1
      			StackPush(&st, right);
      			StackPush(&st, keyi + 1);
      		}
      		if (left