动态规划课堂2-----路径问题

目录

引言：

例题1：不同路径

例题2：不同路径II

例题3：礼物的最⼤价值

例题4：下降路径最⼩和

例题5：最小路径和

结语：

引言：

在学习完动态规划斐波那契数列模型后，相信大家对动态规划已经有了一定的了解，下面我们继续深入学习动态规划的路径问题，我们一般的解题步骤还是1. 状态表示，2.状态转移方程，3.初始化，4.填表顺序，5.返回值。在写代码时一定要把这5步考虑清楚再写代码，写代码的步骤为1.创建 dp表2.初始化3.填表4.返回值。

例题1：不同路径

链接：不同路径

题目简介：

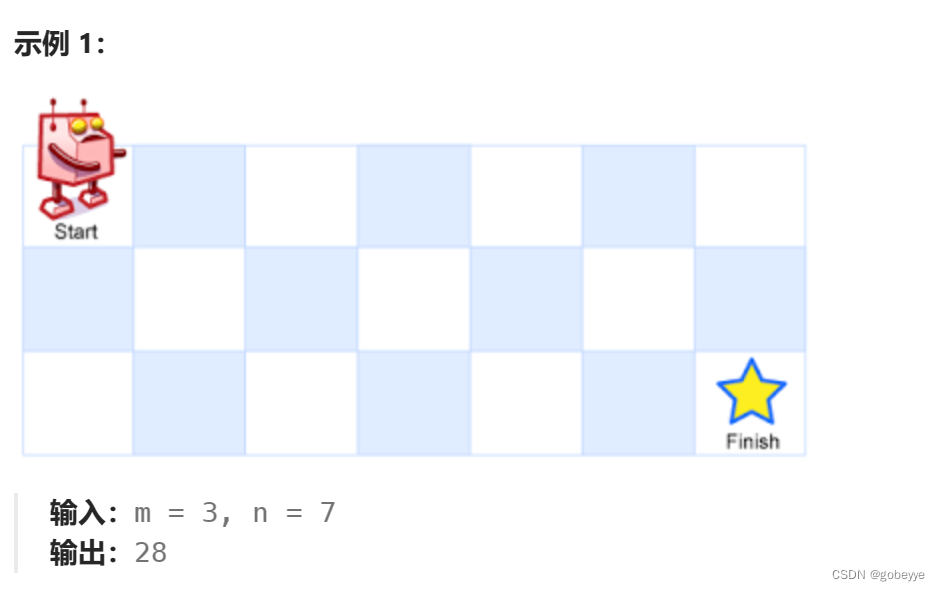
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

解法（动态规划）：

1. 状态表示：

对于这种「路径类」的问题，我们的状态表⽰⼀般有两种形式：

（1）从[i, j] 位置出发到终点有几种路径。

（2）从起始位置出发，到达[i, j] 位置有几种路径。

本题我们选择第二种，dp[i][j] 表示：⾛到[i, j] 位置处，⼀共有多少种⽅式。

2.状态转移方程

简单分析⼀下。如果dp[i][j] 表⽰到达[i, j] 位置的⽅法数，那么到达[i, j] 位置之 前的⼀⼩步，有两种情况：

（1）从[i, j] 位置的上⽅（ [i - 1, j] 的位置）向下⾛⼀步，转移到[i, j] 位置

（2）从[i, j] 位置的左⽅（ [i, j - 1] 的位置）向右⾛⼀步，转移到[i, j] 位置。

由于我们要求的是有多少种⽅法，因此状态转移⽅程就呼之欲出了： dp[i][j] = dp[i - 1] [j] + dp[i][j - 1] 。

3.初始化

使用辅助结点 。

注意点：（1）辅助结点⾥⾯的值要「保证后续填表是正确的」（2）下标的映射关系。在本题中，「添加⼀⾏」，并且「添加⼀列」后，只需将dp[0][1] 的位置初始化为1 即可。

4.填表顺序

根据「状态转移⽅程」的推导来看，填表的顺序就是「从上往下」填每⼀⾏，在填写每⼀⾏的时候 「从左往右」。

5.返回值

根据「状态表⽰」，我们要返回dp[m][n]（添加了一个辅助节点） 的值 。

代码如下：

动态规划编写代码的步骤比较固定，上面那5步是想好思路，下面这4步是编写代码的步骤。

class Solution {
    public int uniquePaths(int m, int n) {
        //1.创建dp表
        //2.初始化
        //3.填表
        //4.返回值
        int[][] dp = new int[m + 1][n + 1];
        dp[0][1] = 1;
        for(int i = 1;i