数据结构栈和队列
个人主页:星纭-CSDN博客
系列文章专栏:数据结构
踏上取经路,比抵达灵山更重要!一起努力一起进步!
目录
一.栈
1.栈的介绍
2.初始化与销毁
3.入栈和出栈
4.栈顶元素,判空,求栈的元素个数
代码:
test.c
stack.h:
stack.c:
二.队列
1.队列的介绍
2.初始化与销毁
3.插入与删除
4.查看队头队尾元素
5.判空与队列大小
代码:
一.栈
1.栈的介绍
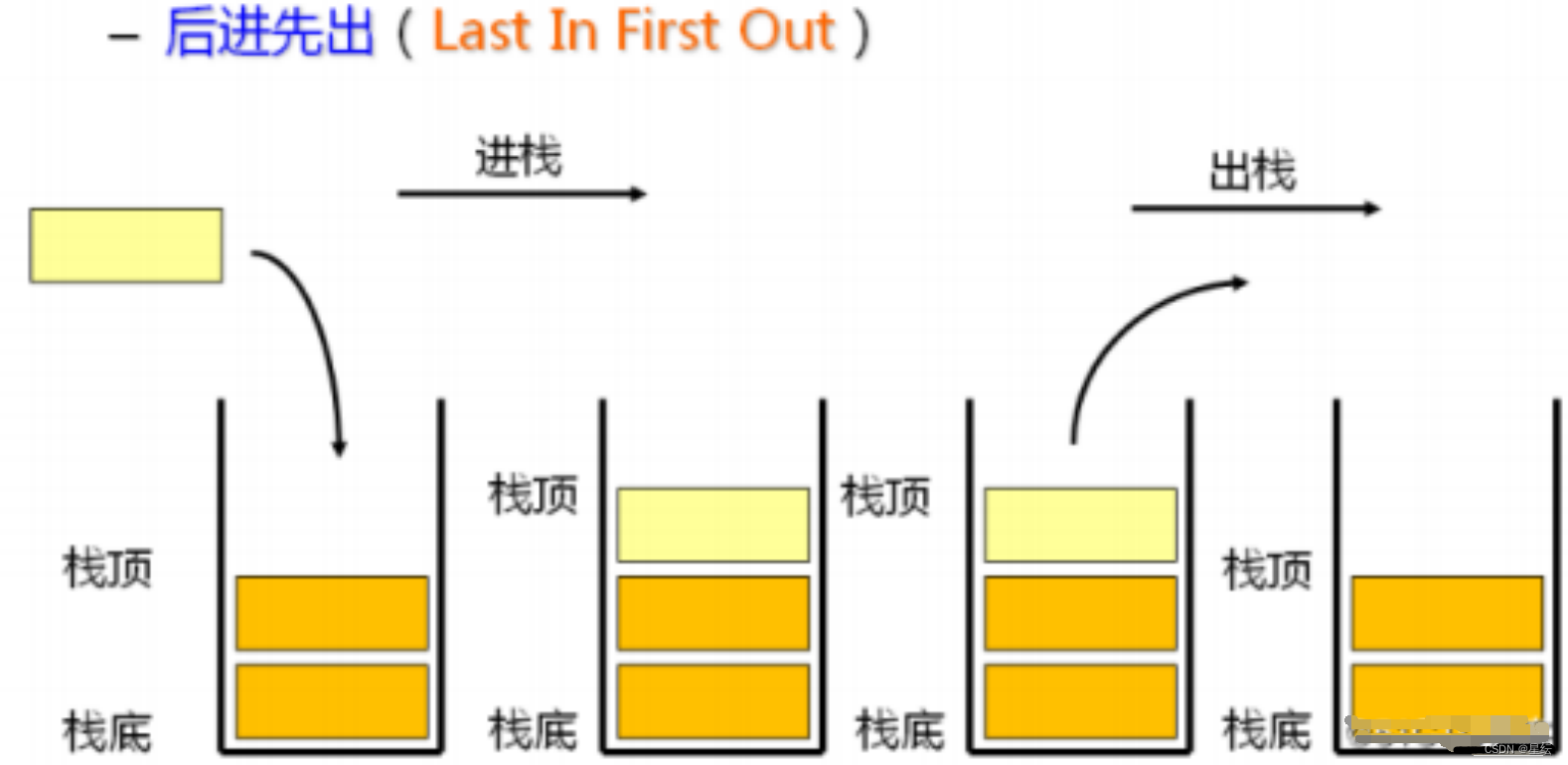
栈是一种线性数据结构,它只能在固定的一端进行插入和删除操作,这一端被称为栈顶,另一端则称为栈底。栈的特点是后进先出(Last In First Out,LIFO),即最后插入的元素最先被删除,而最先插入的元素最后被删除。
栈的基本操作有两个:入栈(push)和出栈(pop)。入栈操作将元素插入到栈顶,出栈操作将栈顶元素删除并返回。
- 入栈:栈插入数据的操作也叫入栈/压栈/进栈,入数据在栈顶。
- 出栈:栈的删除操作也叫做出栈。出数据也在栈顶。
栈可以用来解决一些具有后效性的问题,例如表达式求值、括号匹配、函数调用等。它也可以用于实现一些常见的数据结构,例如递归函数、深度优先搜索等。
栈可以使用数组或链表来实现。使用数组实现的栈称为顺序栈,使用链表实现的栈称为链式栈。无论使用哪种实现方式,栈的空间复杂度都为O(n),其中n为栈中元素的个数。
栈还有一些常见的扩展操作,例如获取栈顶元素(top)、判断栈是否为空(isEmpty)、获取栈中元素个数(size)等。这些操作的时间复杂度都为O(1)。
对于顺序栈来说,又分两种情况:一种是定长的静态栈结构,一般情况下,实际中用的比较少,另一种是支持动态增长的栈。
以下的栈的实现,作者基于支持动态增长的顺序栈完成。
typedef int STDatatype;
typedef struct{
STDatatype* a;
int top;//栈顶
int capacity;//栈的容量
}Stack;
为了方便对存储的数据类型进行更改,我们对int重命名一下,如果以后要存储char类型的数据,只需要更改一下int为char就可以轻松完成。
2.初始化与销毁
//初始化 void STInit(Stack* pst); //销毁 void STDestory(Stack* pst);
1.初始化
void STInit(Stack* pst) {
pst->a = NULL;
pst->capacity = pst->top = 0;
};
因为开始的时候,这个栈中并没有任何的元素,所以我们将其的a初始化为NULL,top和capacity为0.
其实对于top的初始化是有两种情况的:
如果top指向的是栈顶的元素:
比如这样的TOP就是指向栈顶的元素8,此时存放了3个数据,Top的值等于2.
可以是我们开始初始化为0,此时的TOP指向下标为0的位置,可是此时的位置上并没有元素,这里的top指向的是栈顶元素的下一个位置,并不是栈顶元素。
所以如果要使top指向栈顶元素,初始化应该为-1,而不是0.
本文采用top指向栈顶元素的下一个位置。
2.销毁
销毁其实和初始化很类似。
因为a是我们使用malloc函数动态开辟的空间,所以我们需要free释放掉a。
//初始化
void STInit(Stack* pst) {
assert(pst);
pst->a = NULL;
pst->capacity = pst->top = 0;
};
//销毁
void STDestory(Stack* pst) {
assert(pst);
free(pst->a);
pst->a = NULL;
pst->capacity = pst->top = 0;
};
为了防止pst->a时造成野指针,需要对pst进行断言一下,避免pst是NULL.
3.入栈和出栈
1.入栈
在入栈之前,我们需要对栈判断空间是否足够。因为top指向的是栈顶元素的下一个位置,所以当满了的条件是top等于capacity,而对于top指向的是栈顶元素而言,判满的条件是capacity = top + 1.
可是对于这个条件来说,当容量为0的时候,这个条件也成立,所以这里需要使用三目操作符,更改容量,以免乘以2后还是0.用tmp接收开辟的空间是为了避免开辟失败,返回NULL,导致a变成了NULL,使数据丢失。realloc函数当第一个 参数的值为NULL的时候,它的功能和malloc函数一模一样。所以我们不需要单独判断a是否为NULL.
void STPush(Stack * pst,STDatatype x){
assert(pst);
if (pst->top == pst->capacity) {
int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDatatype* tmp = (STDatatype*)realloc(pst->a,newcapacity * sizeof(STDatatype));
if (tmp == NULL)
{
perror("malloc fail");
exit(1);
}
pst->a = tmp;
pst->capacity = newcapacity;
}
pst->a[pst->top++] = x;
};
注意:最后记得top+1,不要忘了。
2.出栈
对于数组而言,出栈的时候,并不需要把这个数据真的移除掉,只需要top--即可,因为这样这个元素实际上就不在这个栈中了,我们再入栈的时候,就会覆盖掉这个元素。
void STPop(Stack* pst) {
assert(pst);
assert(pst->top>0);
pst->top--;
};
出栈要注意,栈空了就不能出栈了。否则top就变成负数了。
4.栈顶元素,判空,求栈的元素个数
//栈顶元素
STDatatype STTop(Stack* pst) {
assert(pst);
assert(pst->top>0);
return pst->a[pst->top - 1];
};
//判空
bool IsEmpty(Stack* pst) {
assert(pst);
return pst->top == 0;
}
//求元素个数
int STSize(Stack* pst) {
assert(pst);
return pst->top;
};
这三个函数非常简单:栈定元素需要保证这个栈不能为空,也就是top要大于0,否则不对。
判空,当栈空的时候top就0,所以只需要判断top等不等于0即可。
求元素个数:因为top指向栈顶元素的下一个位置,又因为数组下标从0开始,所以top就代表元素的个数。
代码:
test.c
#define _CRT_SECURE_NO_WARNINGS
#include"stack.h"
int main()
{
Stack s;
STInit(&s);
STPush(&s,1);
printf("%d->", STTop(&s));
STPush(&s,2);
printf("%d->", STTop(&s));
STPush(&s,3);
printf("%d->", STTop(&s));
STPush(&s,4);
printf("%d->", STTop(&s));
STPush(&s,5);
printf("%d->", STTop(&s));
STPush(&s,6);
printf("%d->", STTop(&s));
printf("\n栈总共有%d个元素\n",STSize(&s));
//打印整个栈的元素
while (!IsEmpty(&s)) {
printf("%d->",STTop(&s));
STPop(&s);
}
printf("\n栈总共有%d个元素\n", STSize(&s));
STDestory(&s);
return 0;
}
输出结果:
stack.h:
#pragma once
#include
#include
#include
#include
//#include
typedef int STDatatype;
typedef struct{
STDatatype* a;
int top;//栈顶
int capacity;//栈的容量
}Stack;
//初始化
void STInit(Stack* pst);
//销毁
void STDestory(Stack* pst);
//入栈
void STPush(Stack* pst, STDatatype x);
//出栈
void STPop(Stack* pst);
//栈顶元素
STDatatype STTop(Stack* pst);
//判空
bool IsEmpty(Stack* pst);
//求元素个数
int STSize(Stack* pst);
stack.c:
#define _CRT_SECURE_NO_WARNINGS
#include"stack.h"
//初始化
void STInit(Stack* pst) {
assert(pst);
pst->a = NULL;
pst->capacity = pst->top = 0;
};
//销毁
void STDestory(Stack* pst) {
assert(pst);
free(pst->a);
pst->a = NULL;
pst->capacity = pst->top = 0;
};
//入栈
void STPush(Stack * pst,STDatatype x){
assert(pst);
if (pst->top == pst->capacity) {
int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDatatype* tmp = (STDatatype*)realloc(pst->a,newcapacity * sizeof(STDatatype));
if (tmp == NULL)
{
perror("malloc fail");
exit(1);
}
pst->a = tmp;
pst->capacity = newcapacity;
}
pst->a[pst->top++] = x;
};
//出栈
void STPop(Stack* pst) {
assert(pst);
assert(pst->top>0);
pst->top--;
};
//栈顶元素
STDatatype STTop(Stack* pst) {
assert(pst);
assert(pst->top>0);
return pst->a[pst->top - 1];
};
//判空
bool IsEmpty(Stack* pst) {
assert(pst);
return pst->top == 0;
}
//求元素个数
int STSize(Stack* pst) {
assert(pst);
return pst->top;
};
二.队列
1.队列的介绍
队列是一种常见的数据结构,它遵循先进先出(FIFO)的原则,只允许在一端(队尾)进行插入数据,在另一端(队头)进行删除数据。队列有两个主要操作:入队(enqueue)和出队(dequeue)。入队将元素添加到队列的末尾,出队将队列的第一个元素删除并返回。
队列与排队类似,有素质的人,不会插队,会从排到队尾,完成事情后,从队头离开。
所以我们,是不能访问中间元素的。
队列通常用于存储需要按照顺序处理的数据。例如,在计算机科学中,可以使用队列来实现广度优先搜索算法(BFS)。
在实现队列时,可以使用数组或链表来存储队列中的元素。数组实现的队列被称为顺序队列,链表实现的队列被称为链式队列。
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,效率会比较低。
本文,作者采用链式队列。
队列的时间复杂度如下:
- 入队:O(1)
- 出队:O(1)
- 查看队首元素:O(1)
队列的空间复杂度为O(n),其中n是队列中的元素数量。
typedef int QDatatype; typedef struct QueueNode { struct QueueNode* next; QDatatype val; }QNode; typedef struct Queue { QNode* phead; QNode* ptail; int size;//节点个数 }Queue;这里采用两个指针分别指向队头与队尾,为了方便,把两个指针与size存放在一个结构体中,这样传参更加的方便。
2.初始化与销毁
1.初始化
最开始时,队列中是没有任何元素的。
//初始化 void QueueInit(Queue* pq) { assert(pq); pq->phead = pq->ptail = NULL; pq->size = 0; };注意观察此处的参数,如果不放在一个结构体 中,那么传参的时候,就需要传递三个指针,大大地增加了使用者的操作难度。开始要断言一下,以免pq为NULL。
2.销毁
//销毁 void QueueDestory(Queue* pq) { assert(pq); QNode* cur = pq->phead; while (cur) { QNode* next = cur->next; free(cur); cur = next; } pq->phead = pq->ptail = NULL; pq->size = 0; };队列的销毁与单链表的销毁很相似,这里不过多介绍。
3.插入与删除
1.插入
插入数据,先malloc动态申请内存来存放这个数据。
然后考虑当这个队列没有元素的时候,phead和ptail指针均指向NULL,这个新插入的节点,即是头节点又是尾节点,所以需要分开讨论。
//队尾插入数据 void QueuePush(Queue* pq, QDatatype x) { QNode* newnode = (QNode*)malloc(sizeof(QNode)); if (newnode == NULL) { perror("malloc fail"); exit(1); } newnode->val = x; newnode->next = NULL; if (pq->phead == NULL) { pq->phead = pq->ptail = newnode; pq->size++; } else { pq->ptail->next = newnode; pq->ptail = newnode; pq->size++; } }当队列为空的时候,就直接将phead与ptail指针指向newnode既可。如果队列不为空就尾插。
2.删除
删除数据,需要释放第一个节点即可,然后让phead指针指向下一个节点。
可是这样写有一个问题,如果此时队列只有一个节点,如果只改变phead的话,ptail仍然指向原来的节点,这样的就会造成野指针了,所以仍然分开讨论。
//队头删除数据 void QueuePop(Queue* pq) { assert(pq); assert(pq->phead); //一个节点 if (pq->phead == pq->ptail) { free(pq->phead); pq->phead = pq->ptail = NULL; }//多个节点 else { QNode* del = pq->phead; pq->phead = pq->phead->next; free(del); del = NULL; } --pq->size; }第二个断言是为了防止队列为空仍然删除数据。
4.查看队头队尾元素
// 取队头和队尾的数据 QDatatype QueueFront(Queue* pq) { assert(pq); assert(pq->size); return pq->phead->val; }; QDatatype QueueBack(Queue* pq) { assert(pq); assert(pq->size); return pq->ptail->val; };在查看之前,首先要确定这个队列中有元素,否则不能查看
5.判空与队列大小
int QueueSize(Queue* pq) { assert(pq); return pq->size; }; bool QueueEmpty(Queue* pq) { assert(pq); return pq->size == 0; };判空与队列大小很简单这里就不过多讲解。
代码:
Queue.h:
#pragma once #include #include #include #include typedef int QDatatype; typedef struct QueueNode { struct QueueNode* next; QDatatype val; }QNode; typedef struct Queue { QNode* phead; QNode* ptail; int size; }Queue; //初始化与销毁 void QueueInit(Queue* pq); void QueueDestory(Queue* pq); //队尾插入数据/队头删除数据 void QueuePush(Queue* pq,QDatatype x); void QueuePop(Queue* pq); // 取队头和队尾的数据 QDatatype QueueFront(Queue* pq); QDatatype QueueBack(Queue* pq); //判空与队列大小 int QueueSize(Queue* pq); bool QueueEmpty(Queue* pq);Queue.c:
#define _CRT_SECURE_NO_WARNINGS #include"queue.h" //初始化 void QueueInit(Queue* pq) { assert(pq); pq->phead = pq->ptail = NULL; pq->size = 0; }; //销毁 void QueueDestory(Queue* pq) { assert(pq); QNode* cur = pq->phead; while (cur) { QNode* next = cur->next; free(cur); cur = next; } pq->phead = pq->ptail = NULL; pq->size = 0; }; //队尾插入数据 void QueuePush(Queue* pq, QDatatype x) { QNode* newnode = (QNode*)malloc(sizeof(QNode)); if (newnode == NULL) { perror("malloc fail"); exit(1); } newnode->val = x; newnode->next = NULL; if (pq->phead == NULL) { pq->phead = pq->ptail = newnode; pq->size++; } else { pq->ptail->next = newnode; pq->ptail = newnode; pq->size++; } } //队头删除数据 void QueuePop(Queue* pq) { assert(pq); assert(pq->phead); //一个节点 if (pq->phead == pq->ptail) { free(pq->phead); pq->phead = pq->ptail = NULL; }//多个节点 else { QNode* del = pq->phead; pq->phead = pq->phead->next; free(del); del = NULL; } --pq->size; } // 取队头和队尾的数据 QDatatype QueueFront(Queue* pq) { assert(pq); assert(pq->size); return pq->phead->val; }; QDatatype QueueBack(Queue* pq) { assert(pq); assert(pq->size); return pq->ptail->val; }; int QueueSize(Queue* pq) { assert(pq); return pq->size; }; bool QueueEmpty(Queue* pq) { assert(pq); return pq->size == 0; };另外扩展了解一下,实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型时可以就会使用循环队列。环形队列可以使用数组实现,也可以使用循环链表完成。循环队列与双端队列,下一篇文章讲解。