【algorithm】算法基础课---二分查找算法（附笔记 | 建议收藏）

🚀write in front🚀

📝个人主页：认真写博客的夏目浅石.

🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝

📣系列专栏：AcWing算法学习笔记

💬总结：希望你看完之后，能对你有所帮助，不足请指正！共同学习交流 🖊

✉️如果无聊的话，就来逛逛我的博客栈吧stack-frame.cn

文章目录

• 前言
• 一、二分查找的思想
• 二、二分查找的模板
• • 1.寻找⼀个数（基本的⼆分搜索）
  • 2.边界问题
  • 3.寻找左侧边界的⼆分搜索
  • 4.寻找右侧边界的⼆分查找
  • 三、经典题目集
  • • 总结

      ---

      前言

      

      关于我写这篇博客的目的以及原因

      其实很早前我就写过博客关于二分法，但是我是不满意的或是我觉得不完美的，于是寒假我又花费三天时间又学了一次，今天就把我所学到的经验和知识输出出来，以供复习和学习。

      声明：这里知识基于算法小抄与深入浅出的程序设计两本书+AcWing算法课（侵权删）

      ---

      提示：以下是本篇文章正文内容，下面案例可供参考

      一、二分查找的思想

      由于找一个数遍历的时间复杂度有些题目会超时，所以就需要一个更加优秀的算法—二分查找算法，其实二分算法可以将时间复杂度缩小到logN 想一想为什么？

      那么废话不多说，下面就来讲二分查找的基本思想：

      我们开始定义两个变量，left，right分别指向数组的左端点和右端点（这里会出现左闭右开以及都是闭区间的边界问题，这个问题下面单独会讲解，大家不用着急）

      利用数学上边的二分法就是一次检查一半，这样就可以一次去除一半的不符合要求的数据，大大加大了效率，通过不断地迭代，进而二分出正确答案。

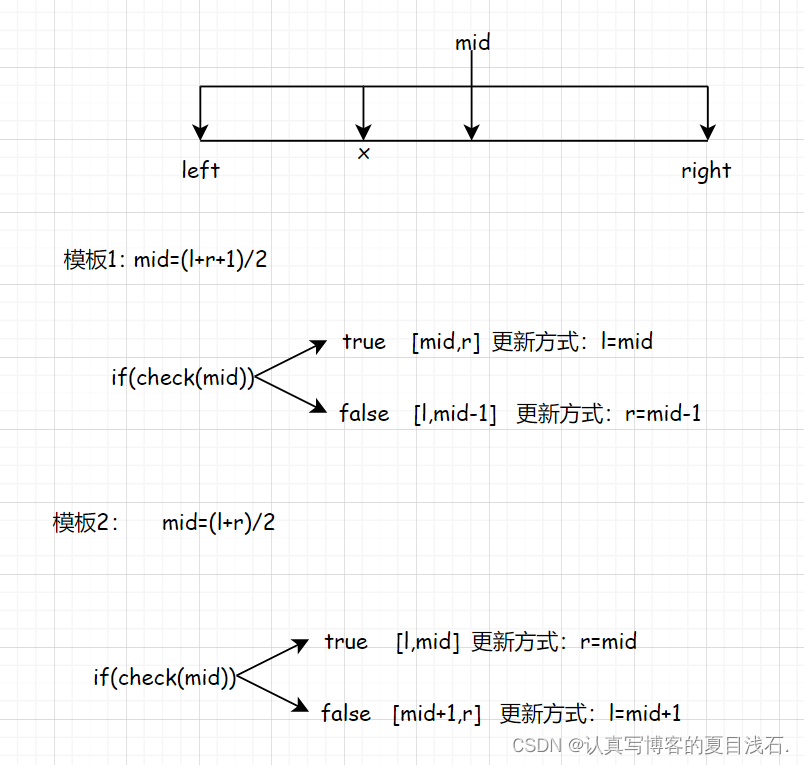
      二、二分查找的模板

      1.寻找⼀个数（基本的⼆分搜索）

      这个场景是最简单的，肯能也是⼤家最熟悉的，即搜索⼀个数，如果存在，

      返回其索引，否则返回 -1。

      

      这里再把二分模板的代码附上：

      这里是一个左闭右开区间

      					//数组 		//目标    //数组长度 
      int binarySearch(int* nums, int target, int size)
      {
      	//特殊情况，可以了解一下这里不计入模板 
      	//if(nums==NULL||size==0)
      	//	return -1;
      	
      	int left=0,right=size-1;
      	while(left
      		int mid=left+(right-left)/2;//防止溢出
      		if(nums[mid]=target) r=mid;
      		else l=mid+1;
      	}
      	if(nums[left]!=target) return -1;
      	else return left; 
      }
      

      这里是一个左右都闭的方法

      					//数组 		//目标    //数组长度 
      int binarySearch(int* nums, int target, int size)
      {
      	//特殊情况，可以了解一下这里不计入模板 
      	//if(nums==NULL||size==0)
      	//return -1;
      	
      	int left=0,right=size-1;
      	while(left
      		if(nums[mid] == target)
      			return mid;
      		else if (nums[mid]  
      2.边界问题
       
       1、为什么 while 循环的条件中是 
      // ...
      }
      return nums[left] == target ? left : -1;
      
      	//特殊情况，可以了解一下这里不计入模板 
      	//if(nums==NULL||size==0)
      	//	return -1;
      	
      	int left=0,right=size;//注意
      	while(left
      		int mid=left+(right-left)/2;//防止溢出
      		if(nums[mid]=target) r=mid;
      		else l=mid+1;
      	}
      	if(nums[left]!=target) return -1;
      	else return left; 
      }
      
      	int left = 0, right = nums.length - 1;
      	// 搜索区间为 [left, right]
      	while (left 	
      		int mid = left + (right - left) / 2;
      		if (nums[mid]