优先级队列（堆）学的好，头发掉的少(Java版)
本篇会加入个人的所谓鱼式疯言
❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言
而是理解过并总结出来通俗易懂的大白话,
小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的.
🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人能接受我们这个概念 ！！！
我们深知，在这个多元化的时代，每个人的兴趣与偏好都独一无二。
因此，我们精心挑选了各类题材，从深邃的宇宙奥秘到细腻的日常生活琐事，从古老的文明遗迹到未来的科技幻想，力求满足每一位读者的好奇心与求知欲。
我们相信，每一个有趣的灵魂都能在这里找到属于自己的那片天空，与作者进行跨越时空的对话，享受阅读带来的纯粹快乐。
前言
提及优先级队列，就会 回忆起我们之前学习过的队列
并且我们提及过 队列 ，队列是一种 先入先出 的数据结构， 但是不能考虑数据本身优先级的高低，那该怎么办呢？
在上篇文章中我们主要讲解了传说中 地狱级别难 其实 也没有那么难 的的二叉树， 而在本篇中也是讲解和二叉树相同的 树状的结构 的 优先级队列，我们也称之为 堆 的一种 数据结构 。
提及难度的话，小伙伴这点可以放心， 当然是不及 二叉树 的 💖 💖 💖 💖
关于 堆 的定义和特性，如何创建 堆 并通过调整维护好这个 堆 的各种方法，小编都会在本篇文章中重点讲解。
目录
-
堆的初识
-
堆的调整
-
堆的数据插入和删除
-
堆实现优先级队列
一. 堆的初识
是否有以一种 数据结构 是可以考虑优先级的，就是说当我们需要对某个数据或某个事务进行考虑，就可以做到优先执行
比如当小伙伴打游戏时，把优先级设置为最大的，如果有电话过来，就会优先选择电话接听的提示
、
比如小伙伴正在上课， 不想有消息发过来，就会把消息通知设置为优先级最小的， 这样即使有消息发送过来，也不会受到提示消息。
那么就是它了 ， 我们的 优先级队列（堆） 就可以在我们的根节点表示优先级最大或最小的，就可以进行优先级最大或最小的数据的管理。
1. 堆的简介
. 概念
像上面这种能够有 优先级特性 的，并且 返回 优先级对象 ，并且能够 插入新对象 的我们称之为 优先级队列（堆） 。
2. 存储方式
在我们上一篇二叉树的学习当中，二叉树存储是用链式结构
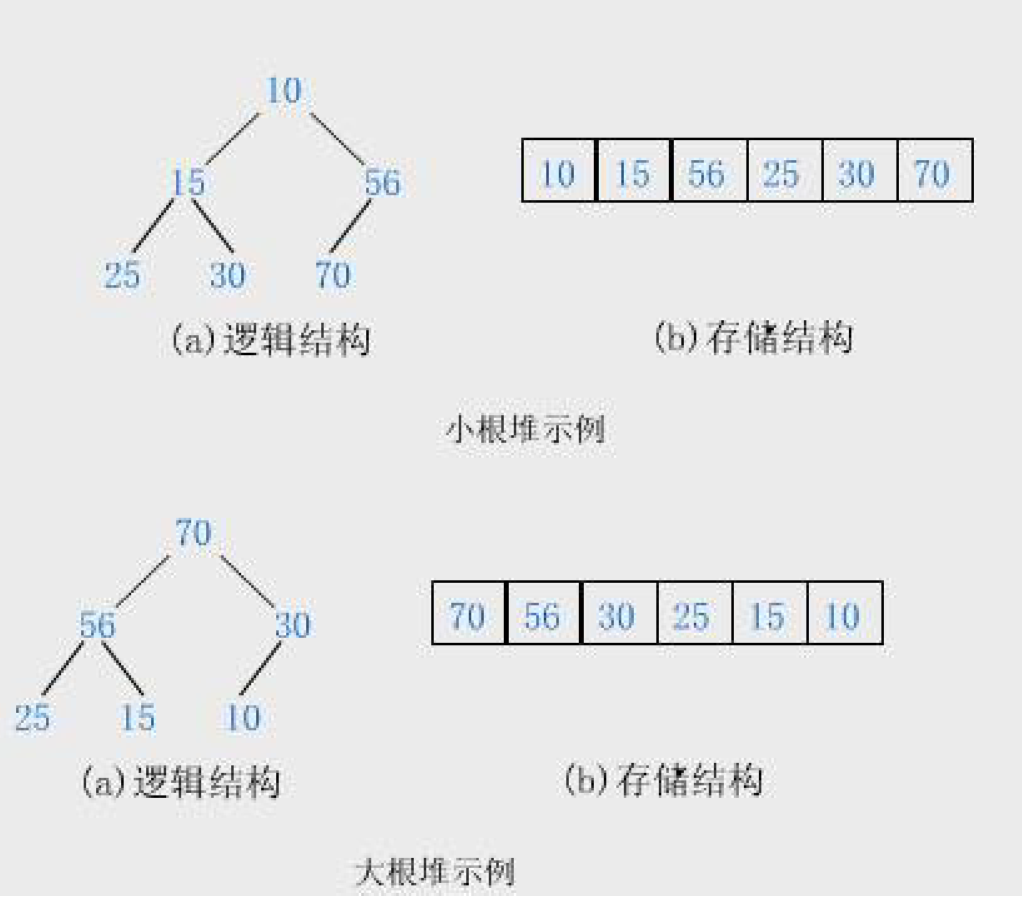
堆的存储方式是顺序结构，也就是说它这些有着优先级的数据是存储在一个一位数组中的。
存储方式有了，我们就需要根据父节点和子节点之间的关系来接替的进行遍历。
具体关系
假设 i 的起始下标为 0
当 i 为子节点 且 i 不为 0 时，我们可以确定 父节点 为 （i - 1）/ 2
当 i 为子节点且 2 * i + 1 不超过最大节点数的下标， 2 * i + 1 为 左子节点
当 i 为子节点且 2 * i + 2 不超过最大节点数 的下标， 2 * i + 2 为 右子节点
鱼式疯言
JDK1.8 的源码中就有 PriorityQueue 这个类为优先级队列，
3. 堆的特性
-
根节点大于或小于子节点
-
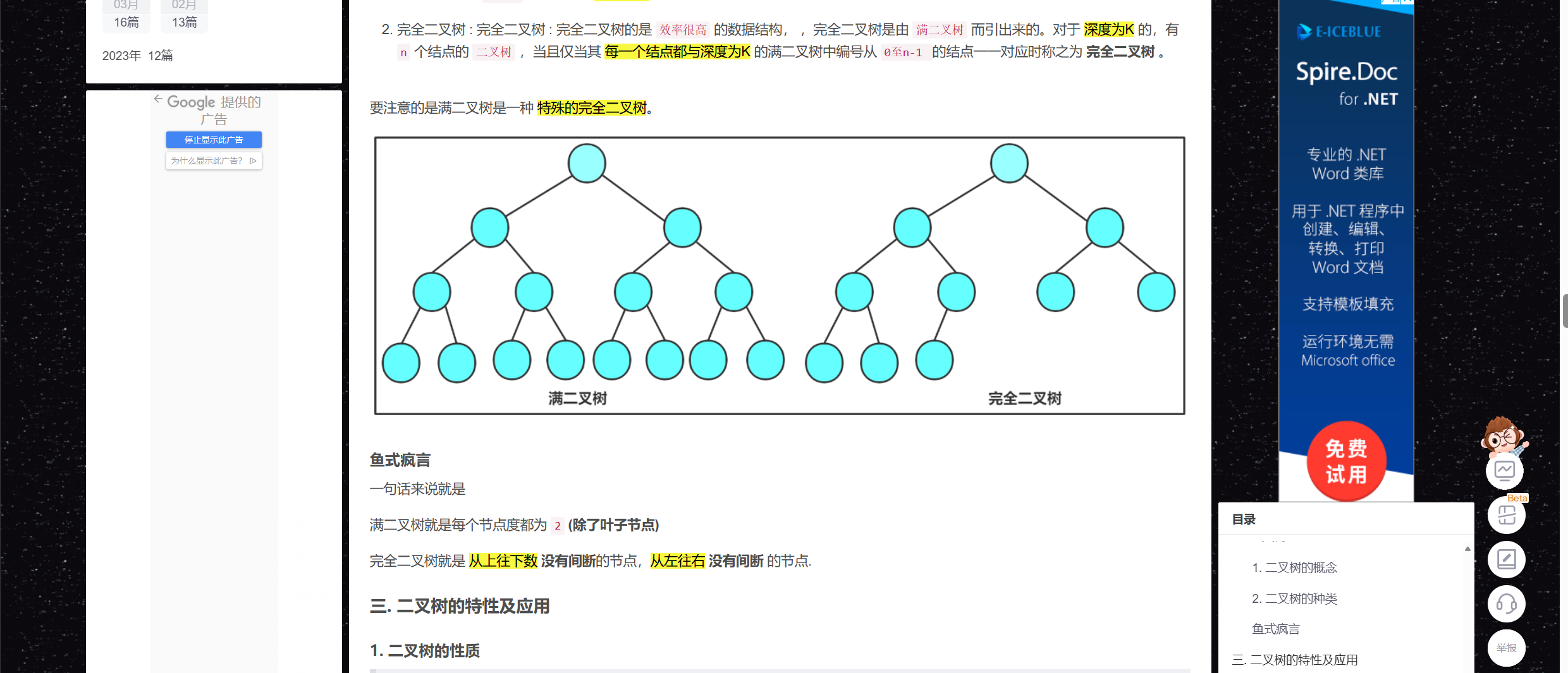
是一颗完全二叉树
1） 根节点大于或小于子节点
我们必须明确的是，只有 根节点 都小于或大于其两边的 子节点 （两边的叶子节点都存在时）
才能实现我们的 优先级对象的返回 。
2) 一颗完全二叉树
上面我们提及堆自身的存储是顺序结构存储的， 所以我们就要构造一颗完全二叉树来管理我们的堆
什么居然有小伙伴们不知道完全二叉树是什么？
完全二叉树学习链接
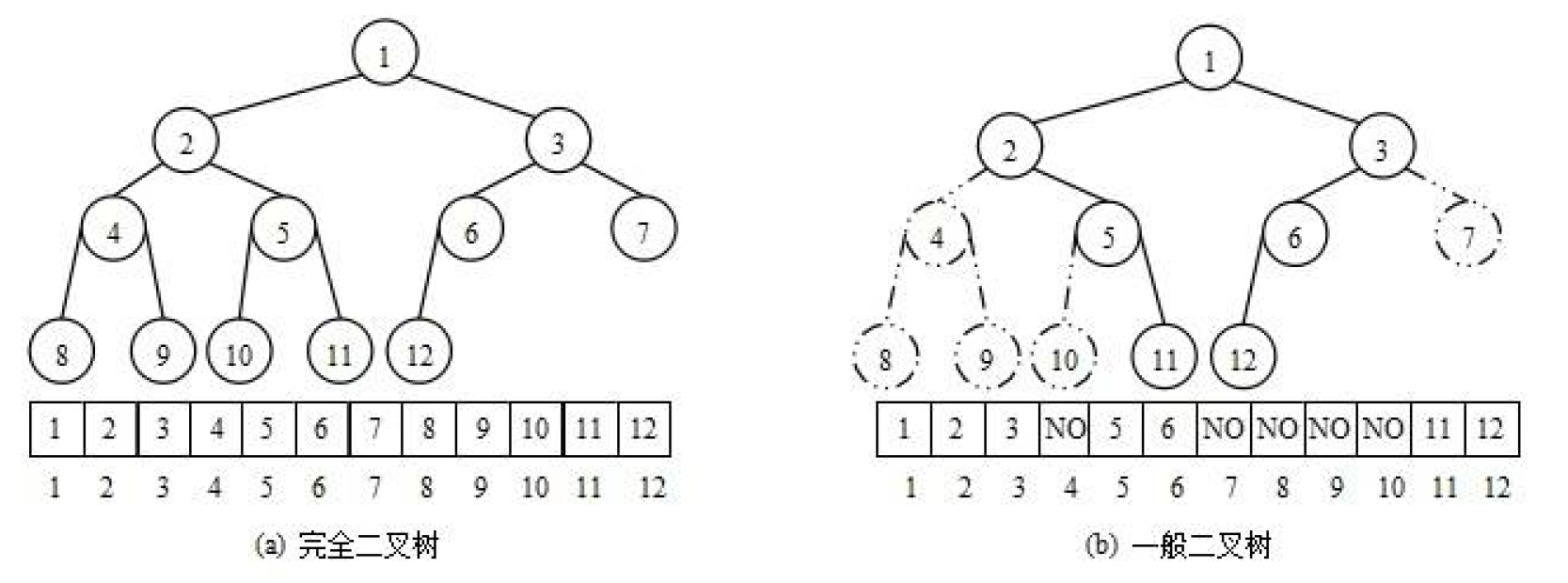
如果不是一颗完全二叉树时，就会出现在一维数组中 有部分为null 的情况
就会出现如下情况 🦊🦊🦊🦊
鱼式疯言
- 解释
这里我们指的 完全二叉树 说的不是我们上篇学习过的二叉树， 而是一种 树型结构 哦，小伙伴们一定要搞清楚。
- 所以上图告诉 小伙伴们
对于 非完全二叉树 来说
因为是 从上往下, 从左往右 存储在 一维数组 中的，就会出现数据分布比较散乱， 既不好集中管理 ，也会 浪费空间 。
所以我们的顺序存储的 堆 就必须严格保证是 完全二叉树
二. 堆的调整
对于堆本身来说，要符合他优先级大或者小的特性，我们就需要通过一些方法来实现。
常用的有两种方法
-
向下调整
-
向上调整
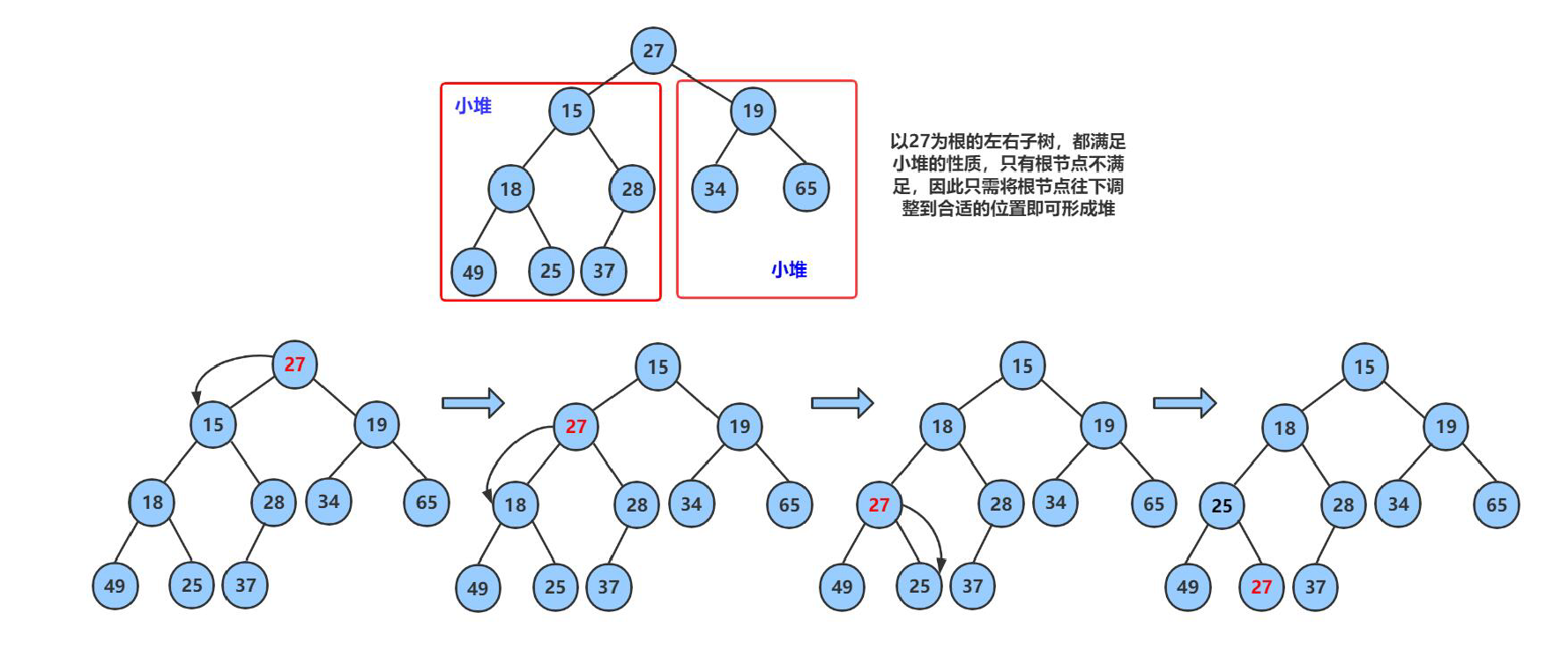
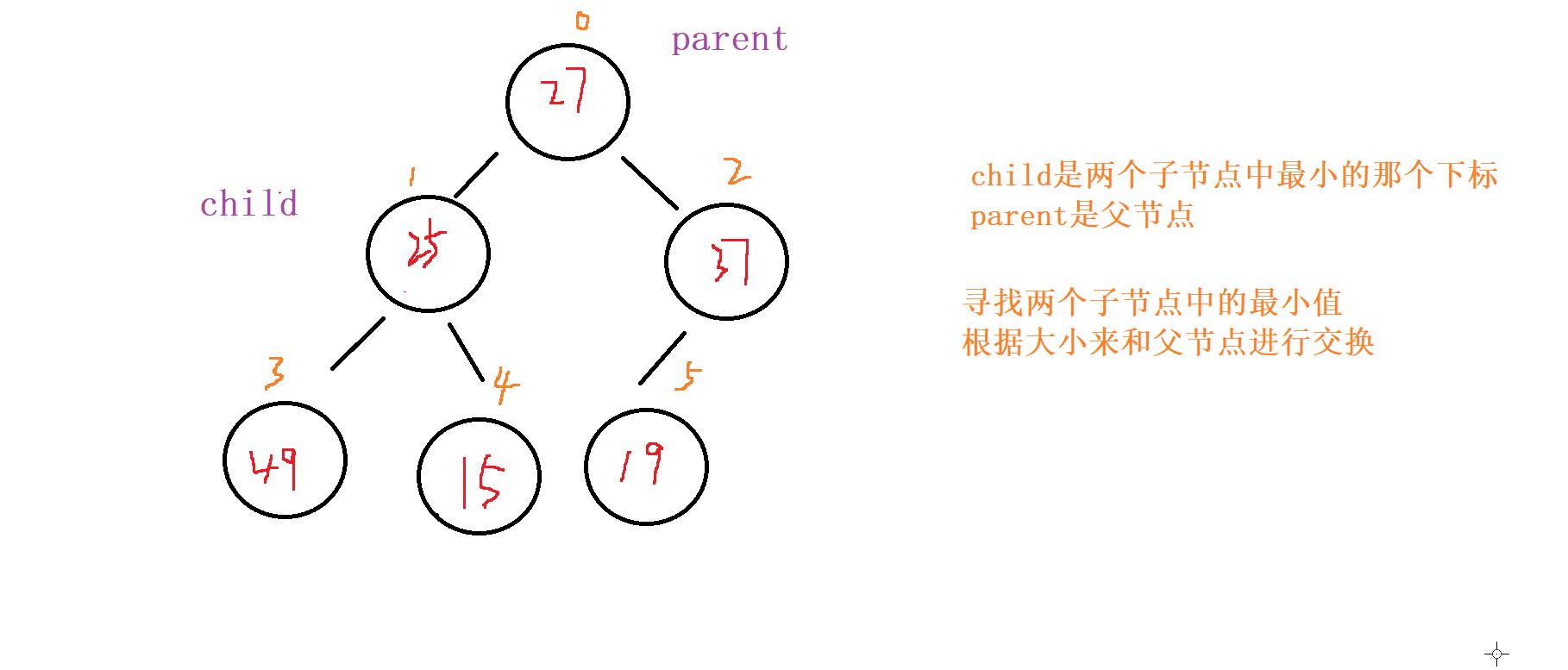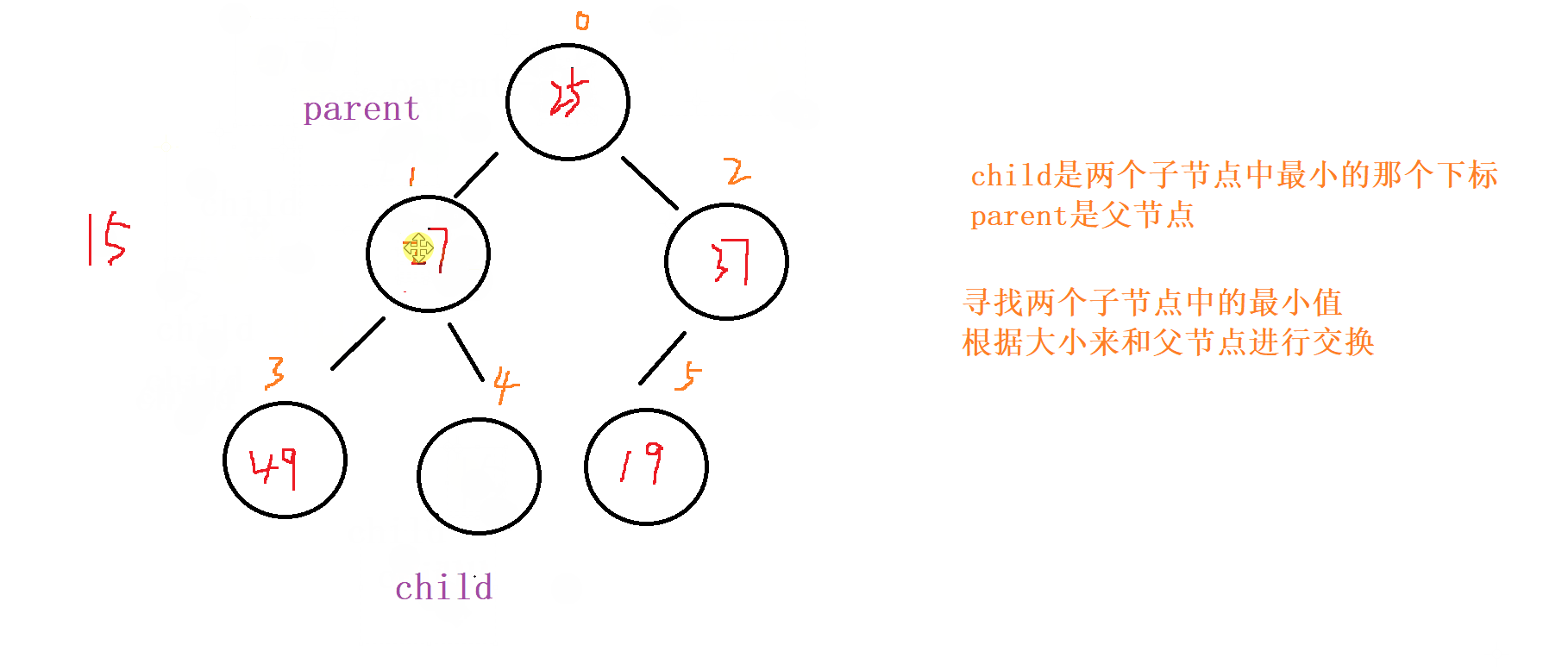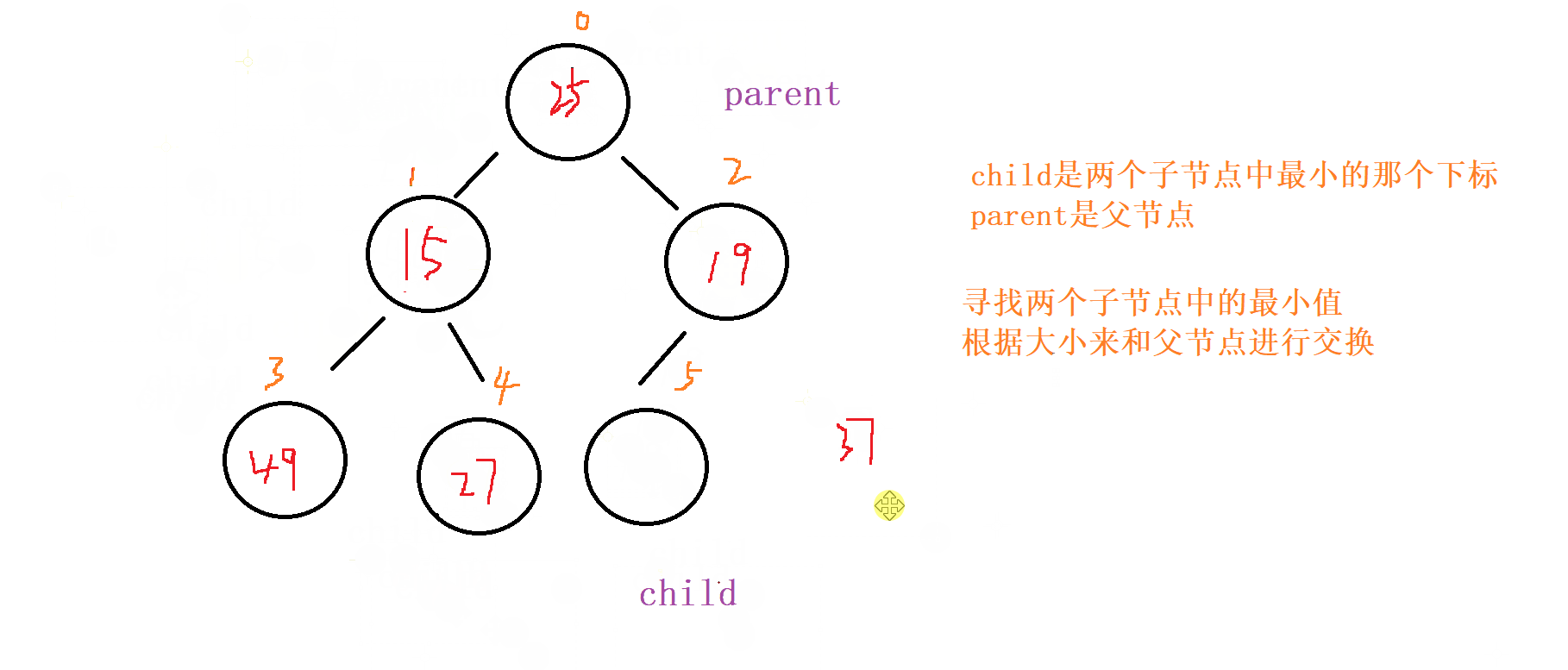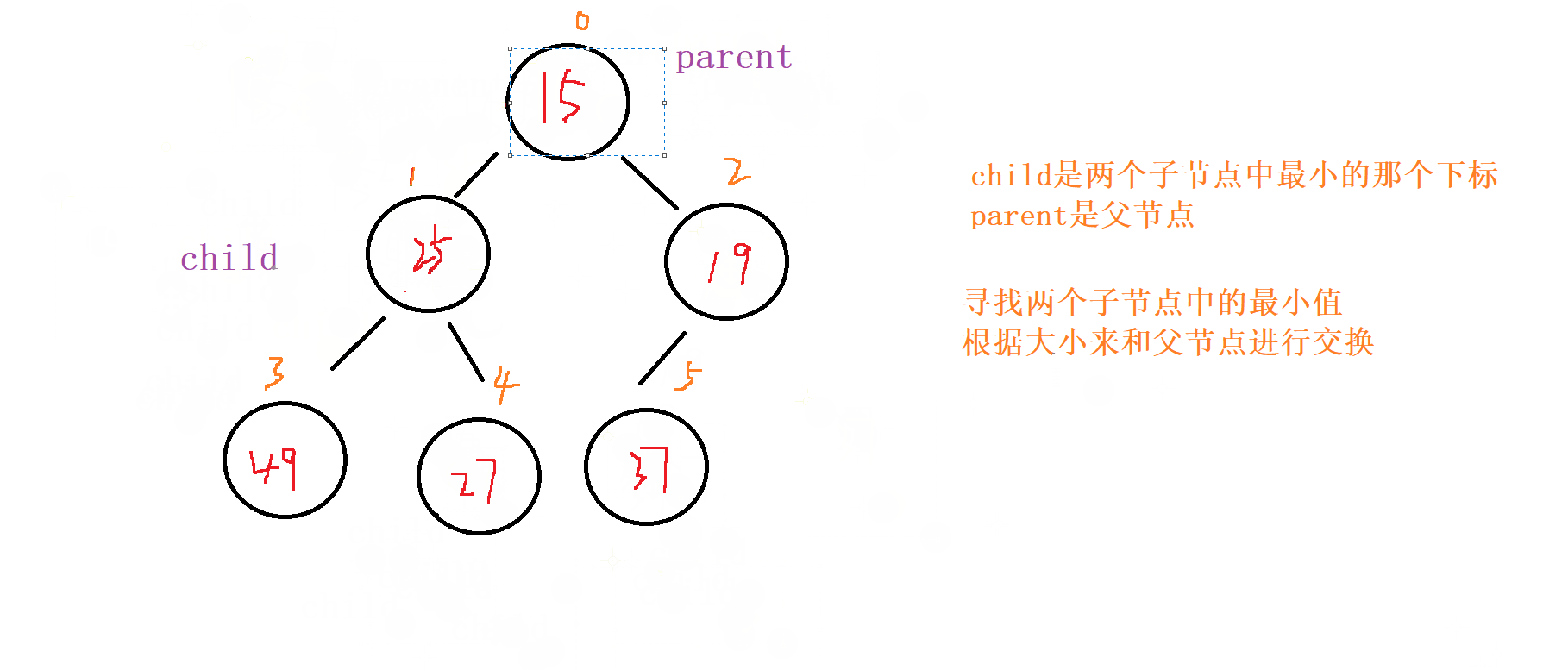
1 . 向下调整
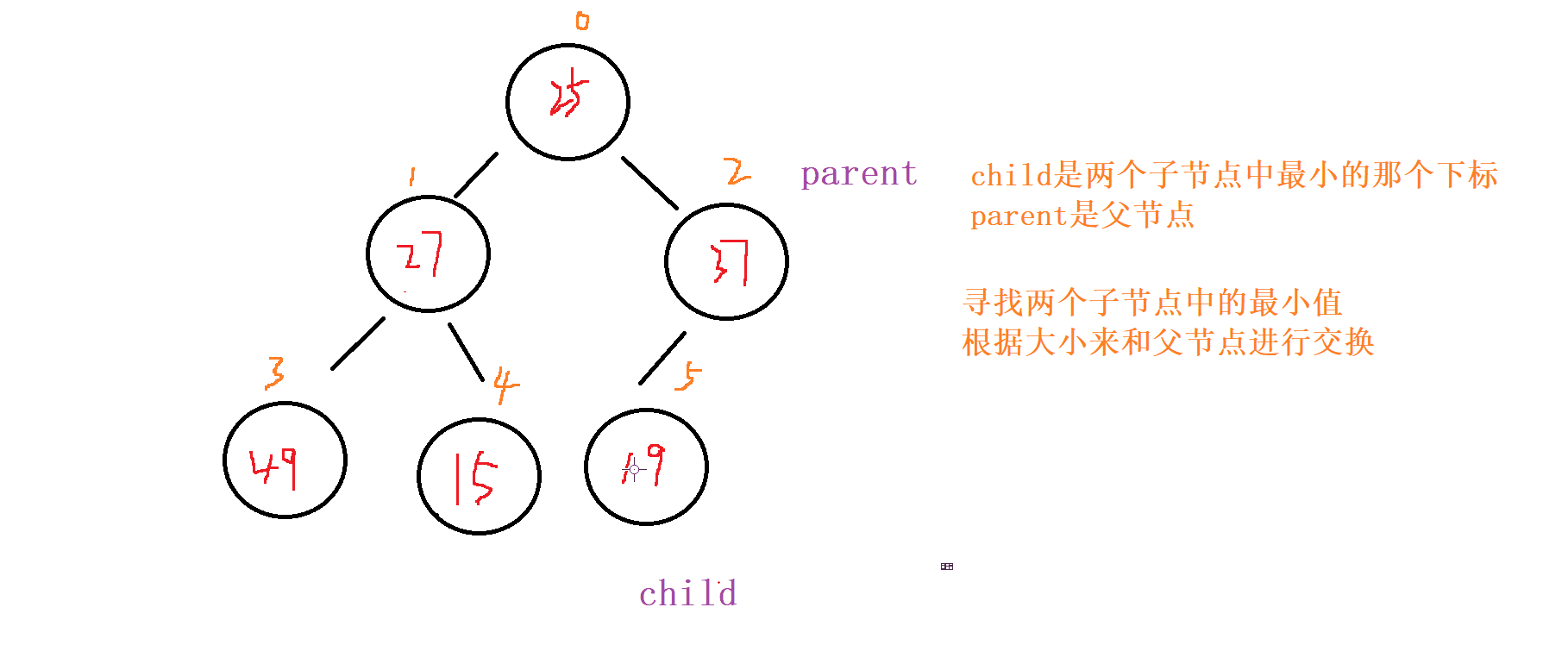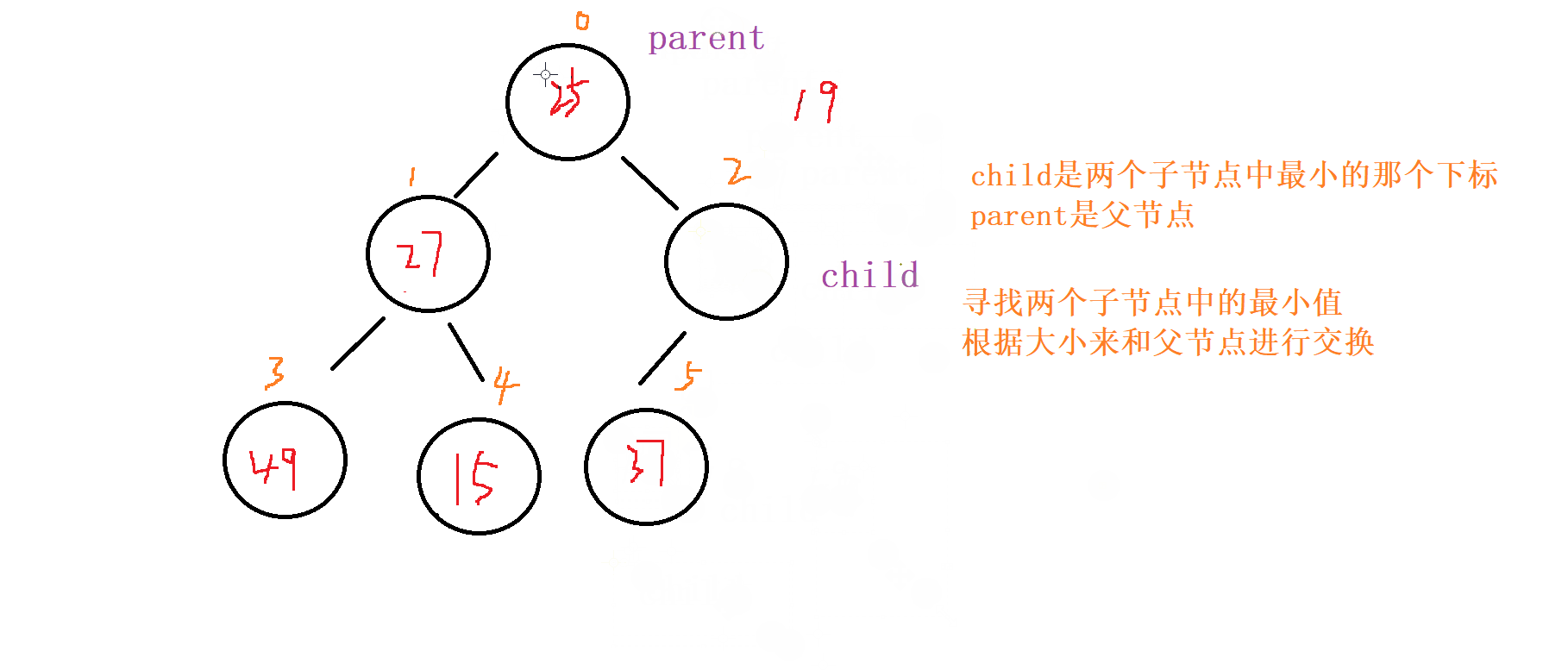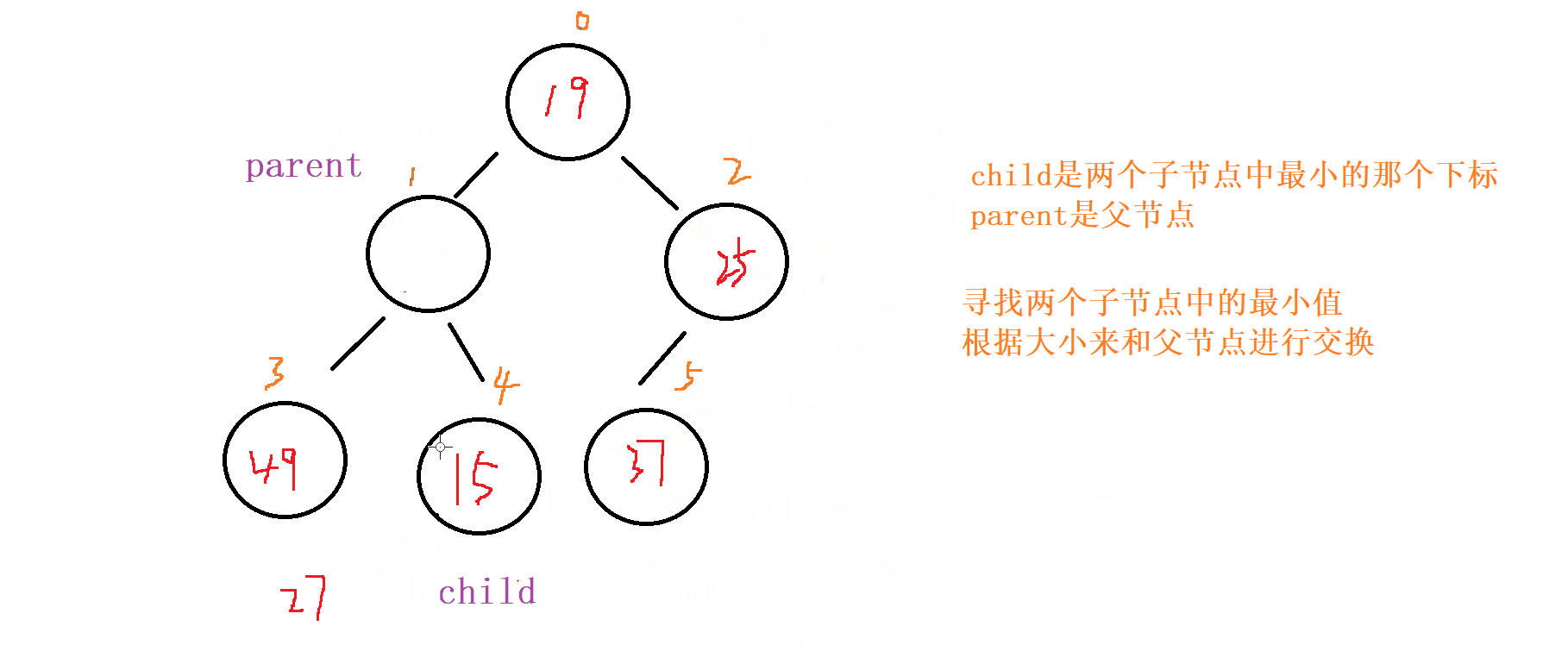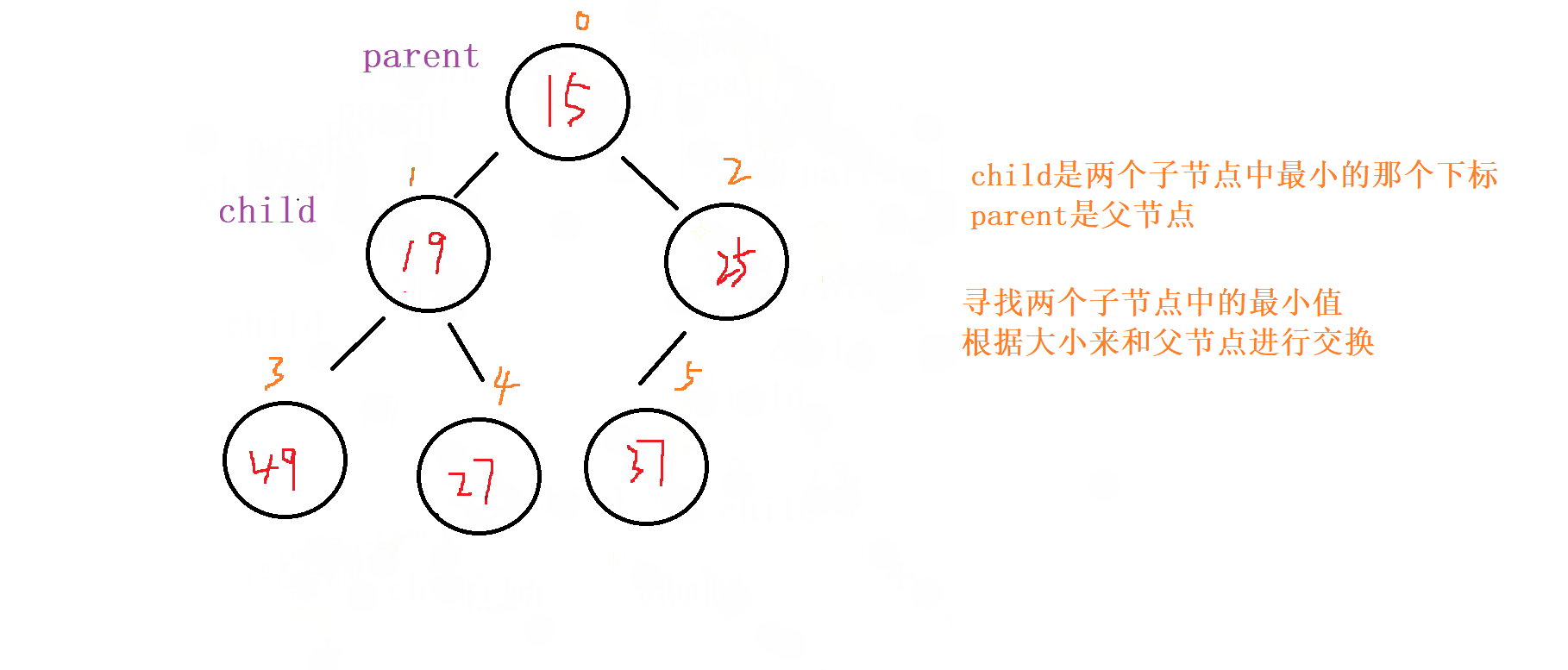
对于向下调整的规则
以 小根堆 为例
-
找出左节点和右节点 两者较小的节点 （如果都存在 的话，不可能只出现右节点，所有只会出现左节点，并且左节点就为最小的 ）
-
如果 父节点 比 子节点 中较小的那个 还小 就成立
否则就讲父节点和 较小节点 进行交换
-
向下调整，讲父节点修改为之前 较小子节点 的位置（child的位置） ，子节点向下走到该子节点的位置 （2*child+1的位置） 再循环进行 比对和调整。
终止条件
-
父节点都要比当前 左右子节点都小
-
遍历完 所有 的 非叶子节点
2. 向上调整
对于向上调整，整体的思路和向上调整差不多
还是以小根堆为例
-
找出左节点和右节点 两者较小的节点 （如果都存在 的话，不可能只出现右节点，所有只会出现左节点，并且左节点就为最小的 ）
-
如果 父节点 比 子节点 中较小的那个 还小 就成立
否则就讲父节点和 较小节点 进行交换
主要区别：
3. 让子节点成为旧父节点， 让旧父节点修改成自身的父节点 （2*parent+1） 。
终止条件
-
父节点都小于左右子节的值
-
父节点
三. 堆的数据插入和删除
我们清楚在队列中我们就有增添(插入)数据， 删除数据。
而我们的堆同时也有 相同的功能 。
1. 数据的插入
. 原理剖析
堆的数据插入必然是在一维数组的最后一位进行插入
那么问题来咯，如果我们插入之后，会不会影响堆的优先级呢，答案是肯定的
所以当我们插入一个数据后，就需要调整，那么我们上面学习过两种调整的方法，该适用于哪一种呢？
相比聪明的小伙伴已经想到了，当然是我们的 向上调整 ，原因很简单
我们是在最后插入的，当我们需要数据的 大小足够大 时，就需要不断的向上调整 ，找到该数组在 完全二叉树中 所处的位置。
. 代码展示
/**
* 入队：仍然要保持是大根堆
* @param val
* 先插入到堆尾
* 利用向上调整为大根堆
*/
public void push(int val) {
if (isFull()) {
elem= Arrays.copyOf(elem,2*elem.length);
}
elem[usedSize]=val;
usedSize++;
int child= usedSize-1;
shiftUp(child);
}
/**
* 想上调整为
* @param child 孩子节点
* 向上调整
* 时间复杂度为 o(N*log(N))
*/
private void shiftUp(int child) {
int parent=(child-1)/2;
while (parent >= 0 && elem[child] > elem[parent]) {
swapElem(elem,parent,child);
child=parent;
parent=(parent-1)/2;
}
}
public boolean isFull() {
return usedSize==elem.length;
}
2. 数据的删除
优先级队列的数据删除，是一种比较巧妙的方式
. 原理剖析
我们既要做到堆顶元素的删除 ，也要保证元素的 个数减少
联想我们学习 顺序表 时，删除最后一个元素只需要把数组 大小-1 即可
那么我们删除堆中的数据，不妨就可以先把 最后一个元素 和 堆顶的第一个元素 进行 交换 ，然后再利用顺序表中的 删除方式 来进行 元素的删除 。
当我们 删除完最后一个元素 也就是堆顶元素时，我们的优先级是不是也发生了改变， 答案也是肯定的
那么我们只需要把最开始我们换到 堆 的那个元素，进行 向下调整 即可，根据 元素大小 的 向下调整 到处在符合条件的优先级位置。
. 代码展示
/**
* 出队【删除】：每次删除的都是优先级高的元素
* 仍然要保持是大根堆
*/
public int pollHeap() {
if (isEmpty()) {
return -1;
}
int ret=elem[0];
swapElem(elem,0,usedSize-1);
usedSize--;
shiftDown(0,usedSize);
return ret;
}
public boolean isEmpty() {
return usedSize==0;
}
四. 堆实现优先级队列
上面对于堆的核心分析
小编认为已经差不多了，下面该是小伙伴们自己 动手实践 的过程了
代码就贴在这里了，小伙们自取哦 💖 💖 💖 💖
1. 代码展示
package PriorityQueue;
import java.util.Arrays;
/**
* Created with IntelliJ IDEA.
* Description:
* User:周次煜
* Date: 2024-04-13
* Time：13:39
*/
public class MyPriorityQueue {
public int[] elem;
public int usedSize;
private static final int FAULTMAXSIZE=10;
public MyPriorityQueue() {
elem=new int[FAULTMAXSIZE];
}
/**
* 建堆的时间复杂度：
*
* @param array
*/
public void createHeap(int[] array) {
usedSize=array.length;
// 初始化堆
for (int i = 0; i = 0 ; i--) {
shiftDown(i,len);
}
}
/**
*
* @param parent 是每棵子树的根节点的下标
* @param len 是每棵子树调整结束的结束条件
* 向下调整的时间复杂度：O(logn)
*/
private void shiftDown(int parent,int len) {
int child=parent*2+1;
while (child+1 elem[parent]) {
if (elem[child] = 0 && elem[child] > elem[parent]) {
swapElem(elem,parent,child);
child=parent;
parent=(parent-1)/2;
}
}
public boolean isFull() {
return usedSize==elem.length;
}
/**
* 出队【删除】：每次删除的都是优先级高的元素
* 仍然要保持是大根堆
*/
public int pollHeap() {
if (isEmpty()) {
return -1;
}
int ret=elem[0];
swapElem(elem,0,usedSize-1);
usedSize--;
shiftDown(0,usedSize);
return ret;
}
public boolean isEmpty() {
return usedSize==0;
}
/**
* 获取堆顶元素
* @return 返回该对顶第一个元素
*/
public int peekHeap() {
if (isEmpty()) {
return -1;
}
return elem[0];
}
public int size() {
return usedSize;
}
}
public class TestPriorityQueue {
public static void main(String[] args) {
int[] array = {2, 4, 5, 8, 9, 10, 11};
MyPriorityQueue mpq = new MyPriorityQueue();
mpq.createHeap(array);
mpq.push(18);
mpq.push(19);
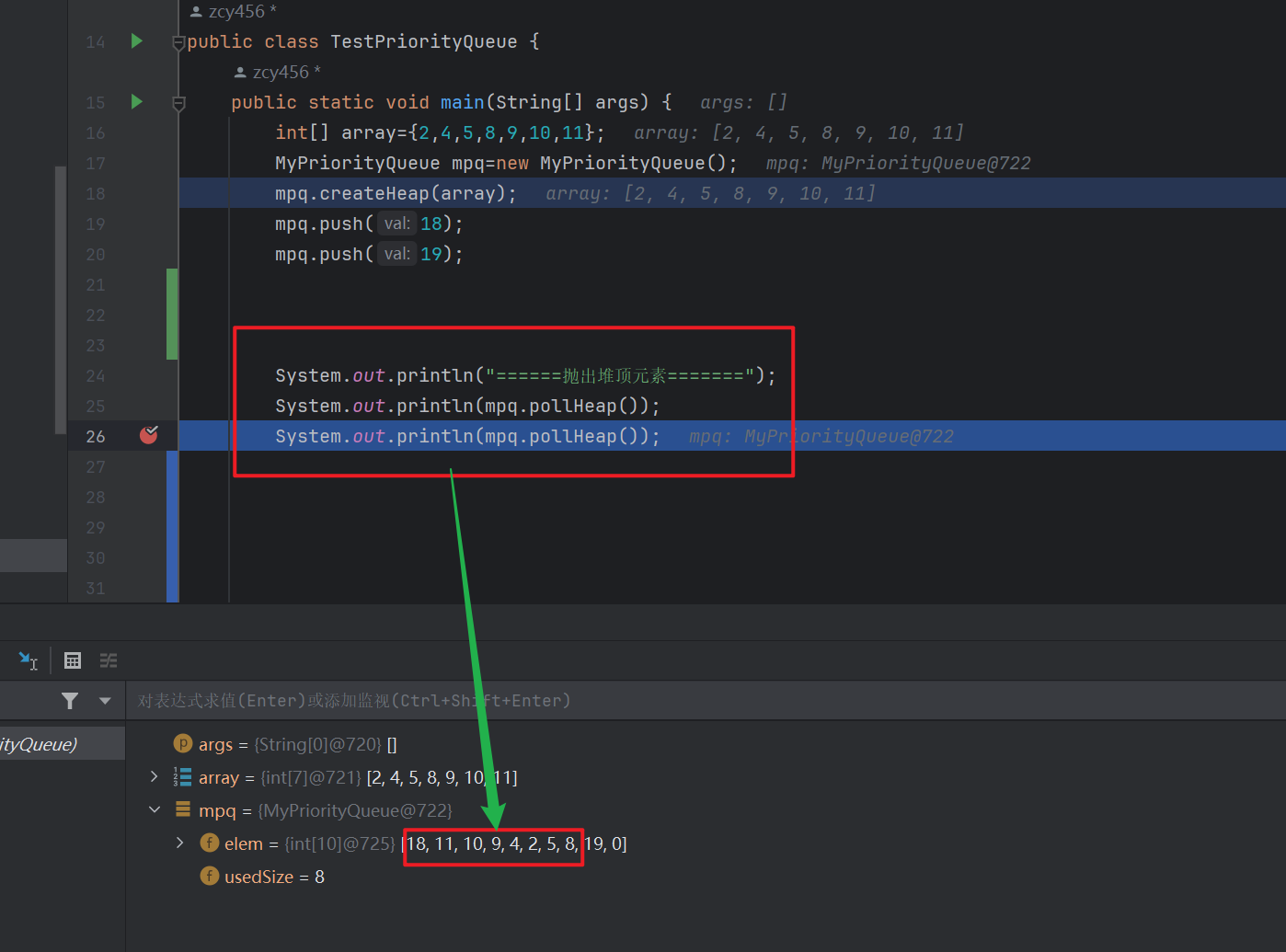
System.out.println("======抛出堆顶元素=======");
System.out.println(mpq.pollHeap());
System.out.println(mpq.pollHeap());
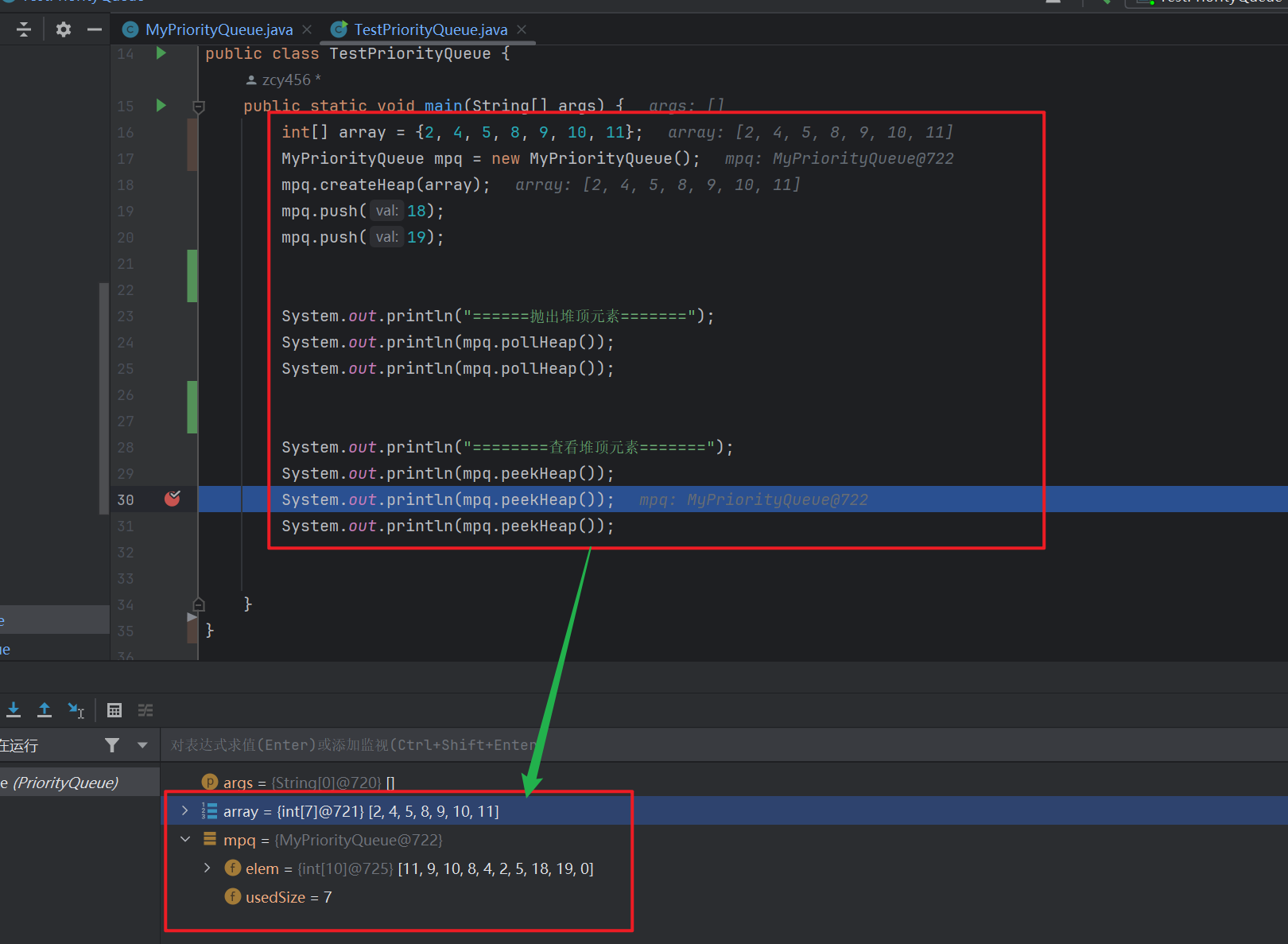
System.out.println("========查看堆顶元素=======");
System.out.println(mpq.peekHeap());
System.out.println(mpq.peekHeap());
System.out.println(mpq.peekHeap());
}
}
鱼式疯言
向上面不仅介绍了直接对 原数组 进行 建堆的方式
public void createHeap(int[] array) {
usedSize=array.length;
// 初始化堆
for (int i = 0; i = 0 ; i--) {
shiftDown(i,len);
}
}
这个的 时间复杂度 为 O( N )
而直接插入的时间复杂度为 O(N*log(N))
public void push(int val) {
if (isFull()) {
elem= Arrays.copyOf(elem,2*elem.length);
}
elem[usedSize]=val;
usedSize++;
int child= usedSize-1;
shiftUp(child);
}
综上所得，建堆的时间复杂度 是 优于 我们的一个一个 插入的时间复杂度 的。
总结
-
堆的初识： 我们认识到了堆本质上一中有着优先级的， 并且融合了完全二叉树和队列的特性，用顺序存储， 一种特殊的树状结构。
-
堆的调整： 向上调整和向下调整各种细节和调整顺序
-
堆的数据插入和删除： 对于插入的场景我们一般用向上调整，对于删除场景， 我们一般向下调整。
-
堆实现优先级队列 ： 从大局中我们用堆实现了优先级队列， 并且从时间复杂度的角度来看，建堆比堆中插入元素更高效。
如果觉得小编写的还不错的咱可支持 三连 下 (定有回访哦) , 不妥当的咱请评论区 指正
希望我的文章能给各位宝子们带来哪怕一点点的收获就是 小编创作 的最大 动力 💖 💖 💖
