数据结构——栈和队列，循环队列，两队列实现栈，两栈实现队列，括号匹配问题

1.栈

1.1栈的概念

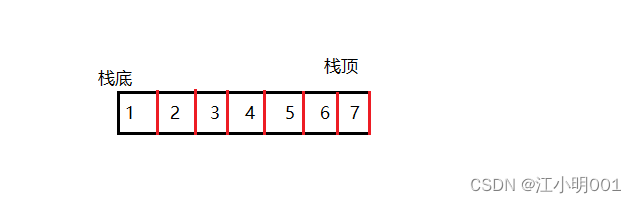
    栈是一种特殊的线性表，其只允许在固定的一端进行插入和删除数据操作。进行数据插入和删除的一端叫做栈顶，另一端叫做栈底。栈的元素遵守后进先出（Last in First out）的原则。

   压栈：数据的插入，也叫做进栈和入栈。

   出栈：数据的删除。

你可以把栈想象成羽毛球桶最后装进去的那个羽毛球，不出意外的话，绝对是第一个被拿出来的

1.2栈的实现

 1.2.1数组实现栈

在栈顶的一端进行数据的插入和删除

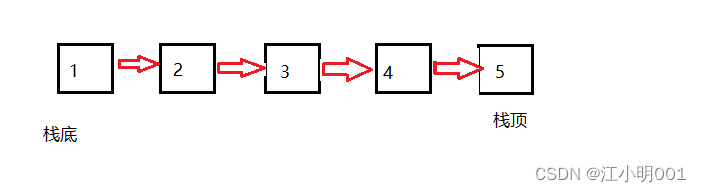
1.2.2单链表实现栈

单链表让尾插那边做栈顶的话，出数据不好出，找不到前一个数据 ，每次都要去遍历链表 ，很麻烦，所以想用单链表实现栈的话最好用头插的方法。

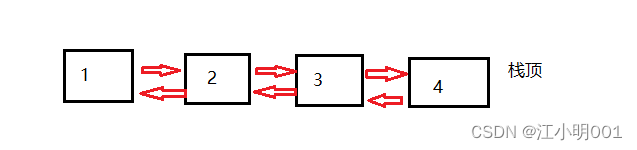
1.2.3双向链表实现栈

双向链表虽然比单链表灵活但是会多开一个空间，所以能用单链表解决的就用单链接表，但有些时候如果很麻烦的话，我们也会不计较这一点空间的浪费。

1.2.4他们之间的对比

 数组实现栈缺点：需要扩容，会造成时间、空间上的浪费。优点：CPU高速缓存很好。

单链表实现数组优点：不需要扩容，做到有多少数据就开多少的空间。缺点：CPU高速缓存不是很好，双向链表，至于能用单向链表的就用单向链表，可以减少空间上的浪费。

所以综上所述，我们可以选择数组或者单量表实现栈，在这里我用数组来实现。

1.2.5栈的实现

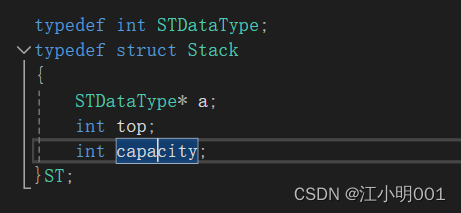
首先我们定义一个栈

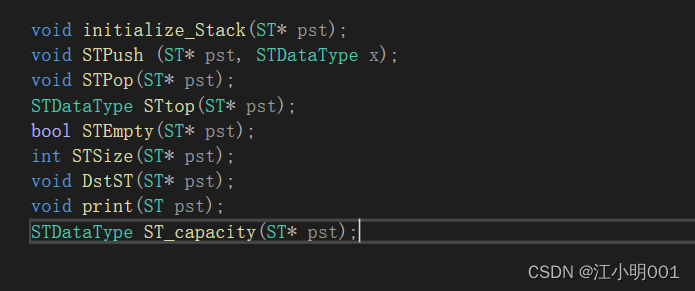
实现栈的一些接口：

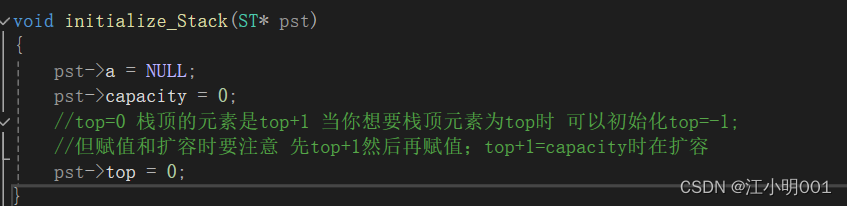
初始化：

这里需要注意一下：你可以先给数组a开空间 pst->a=(STDataType*)malloc(sizeof(STDataType));

但也可以像我一样选择不开；开有开的玩法，不开有不开的玩法。

还有一个就是top的问题，如果你想让top指向的是栈的位置，那么你可以初始化top的值为-1；

这种情况这里的数据为top+1；

当你想让top就是栈里一共有多少元素时 那么top初始化为0；

top的赋值跟我常规化的思维有一定的偏差。这里我初始化top=0；

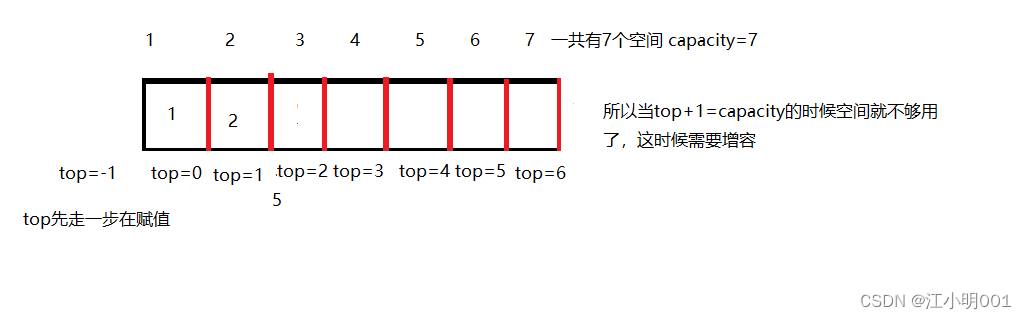
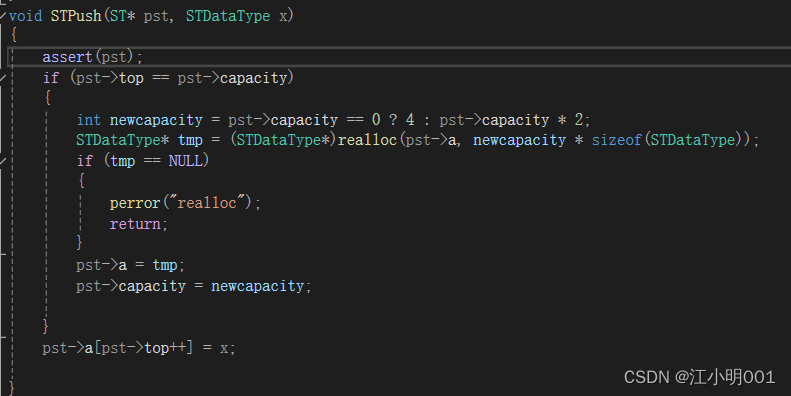
栈的插入：

插入之前我们需要进行空间的大小的判断，如果空间不够那么就要得增大空间，要不然怎

么能在塞数据呢？

扩完容之后我们就在栈顶（数的尾部）进行插入数据就可以了

不会扩容的可以看一下我前面写的动态内存管理，

，

这是我的代码，大家可以参考一下！不过你写的时候不可以偷看我的代码，要自己写才会进步！

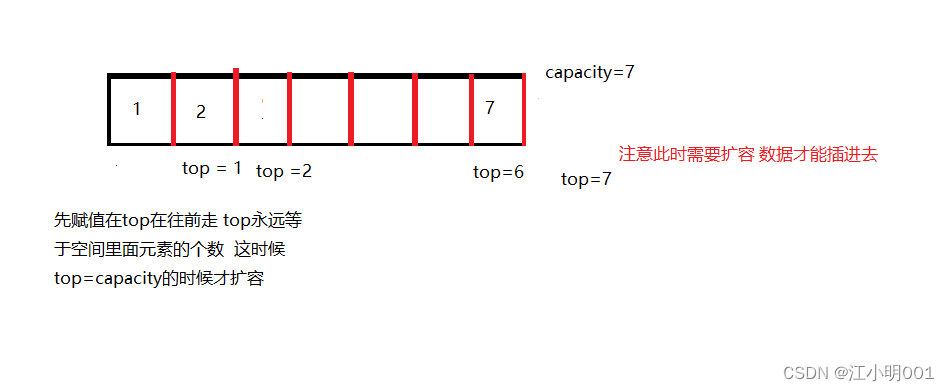
接下来是Pop，对栈的数据删除!你一定要记得栈只能在一端修改数据（栈顶），不要忘记了栈的规则：后进先出

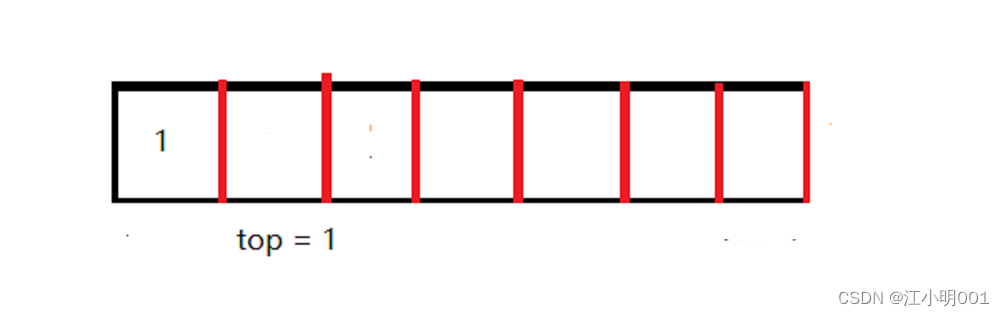
删除就很简单了，只需要将Top--就可以了，你想，当top==0时候是一个数据都没有，当插入一个数据时top==1，也就是Top往前走了一步，而数组里的数据对应的下标是从0开始的，所以，以我这种情况Top==0，往里面插入数据，,想要访问数组里的元素时是不是要要让top-1才能访问到，并且这里top-1就是栈顶的元素了。

差不多就像这样，当你访问数据时反问的是top-1的位置，所以删除数据只需要将top--就行

删除前要记得检测top的值top不能小于1，要不然会越界

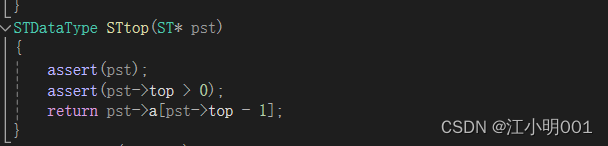
取栈顶的数据：

这个就很好写了，只需要返回栈顶的数据就可以了，而栈顶的数据对应的下标为top-1，当然我这是初始化top为0的时候，当top为-1时，top对应的下标就是栈顶的数据，这个的根据实际情况，

在取数据时也要记得检测数组是不是为空

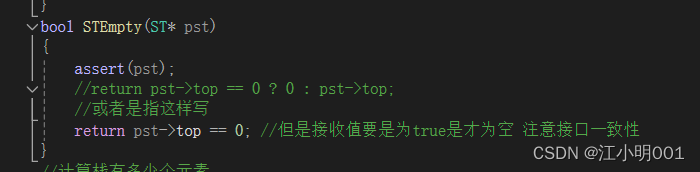
栈的判空：

实际就是检测数组（链表）不为空，为空就放回真，不为空就返回假：

忽视我的注释，注重理解哈。

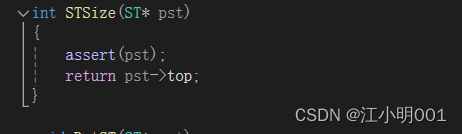
栈里的元素个数就是top的值，所以直接返回top的值就行；

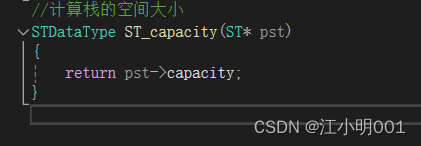
capacity就是空间大小直返回就行

像这样，我们就把栈实现出来了，你也快去试试吧！

2.队列

2.1队列的概念

只允许在一端进行插入数据操作，在另一端进行数据删除操作的特殊性线表队列是先进先FIFO（first in first out）入队列：进行插入数据的一端称为队尾；出队列：进行删除的一端称为对头

2.2队列的用途

队列有绝对的公平性，当你想让某些数据先进先出时，你要想到队列。

比如：QQ的好友推荐，QQ会给你推荐一些陌生的好友，那这些好友是怎么来的呢？

其实这些陌生人是根据你的QQ好友进行推荐给你的，就相当是你好友的好友，如果你有多个好友都有这个陌生人的QQ，那么这位陌生人的QQ推荐度是很高的。

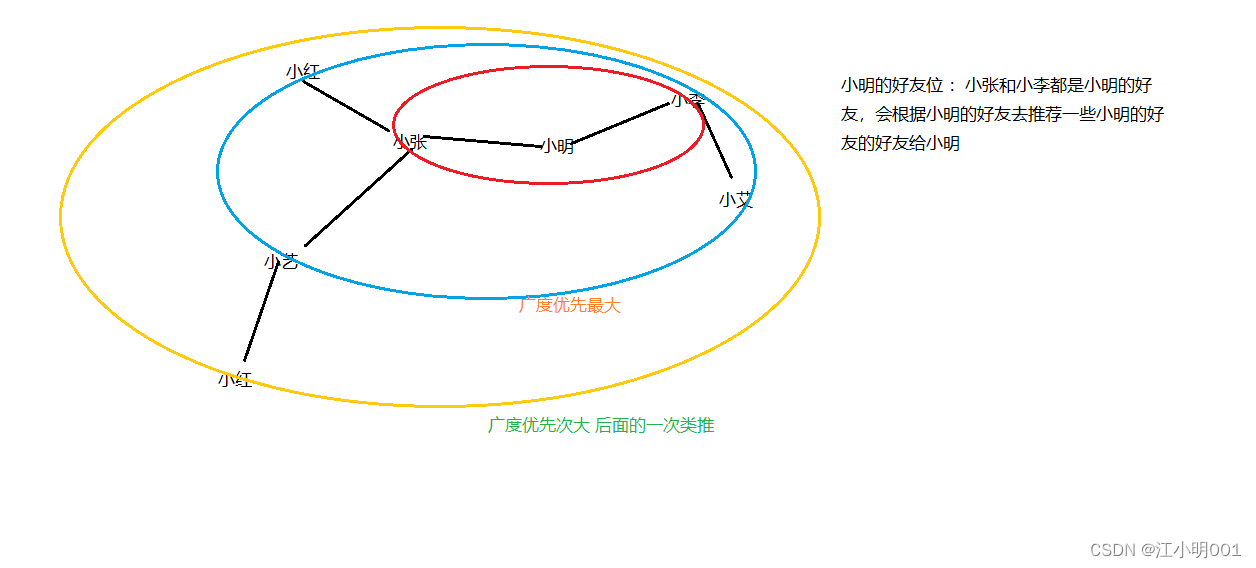
这个就是广度优先问题；

你可以把小明和小明的好友和他的好友的好友全部存在一个队列里，让小明先放其次是他的好友，以此类推，当然这个依然存在一些问题，比如当出小艾的时候你不知是小张还是小李的好友是，所以我们还有对这个算法进行优化，在后面我们会用到树来优化这类问题。所以留个关注，以免找不到我。

2.3队列的实现

好了，看完上面的你是不是也觉得队列很牛，那么接下来我们就一步一步地去实现它

2.3.1队列的构建

队列可以用数组或链表来实现，主要是做到能存储数据并且在一端入数据在另一端出数据的作用就行了，比如你用数组，可以定义两个变量head和tail来指向队头和队尾，入数据时再tail的位置然后++tail出数据时访问的就是head的位置，访问完之后让head++比如你可以这样出数据

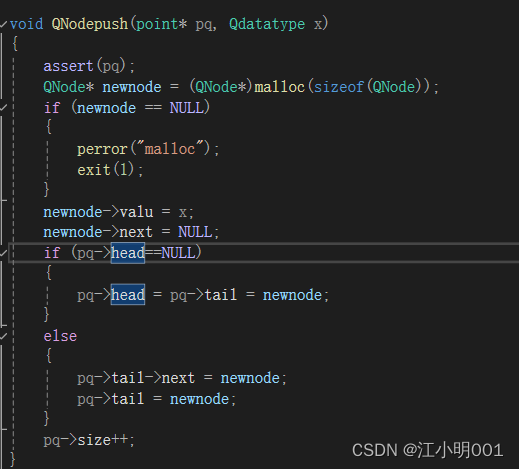
for(int i =head;ihead==NULL）那么就是说明没有一个节点（数据），我们就要去申请一个节点并且让head和tail都指向这个节点

如果有节点的话，直接在tail的后面接上就可以了

对照的上面的图理解；

每次插入数据都要去开开辟一个新的节点，你也可以单独写一个函数出来，创建新节点的时候去调用就可以了。

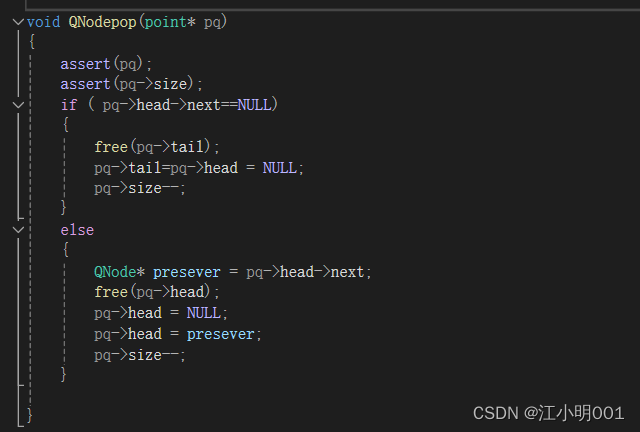
删除

删除和销毁的原理差不多，先存下一个的地址：在把这地址删除就可以了

要注意的是，当只有一个节点的时候，需要把head和tail指针都置为空

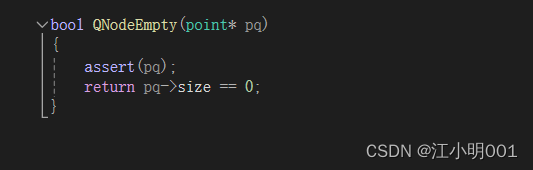
判空：

当个数size为0的时候就是空的所以我们只要返回判断size的值是不是为空的，

返回队头数据：

只需要返回head节点对应的值

返回队尾数据：

返回tail节点对应的值

到这里我们的队列就已经实现出来了。

3.经典题目：

3.1循环队列

循环队列故名思意就是空间可以循环利用；空间大小固定。

就比如排队体侧，如果规定只能进入多少人，如果这个满了，那么就不能再进入了，只有当一些人测完出去了，才能在进人。

那么我们怎样去实现它呢？是用数组呢？还是用链表呢？

当然两个都是可以的哈，只要你能实现的出来：

先来看链表：

单链表实现循环队列：

思路和我们上面创建链表的差不多，但是要多开一个空间，避免假溢出的问题，因为head和tial开始就指向第一个节点，这种情况就是左闭右开，如果你不想额外开空间，那么就要考虑左闭右闭，链表判满很简单，tial的下一个是head就是满，head==tail就为空，或者是在定义一个size去计算队列里的数据，进行判空和判满。难点在于取队尾的数据，队尾的数据=tial-1，但是单链表不好搞，除非你用双向循环链表或者是遍历单链表（这个比较好时，你会选择？）还有一种方法就是在定义一个指针指向tail的前一个节点。这些办法都可以解决。不过各有各自的难度。那我们来看一下数组。

数组：

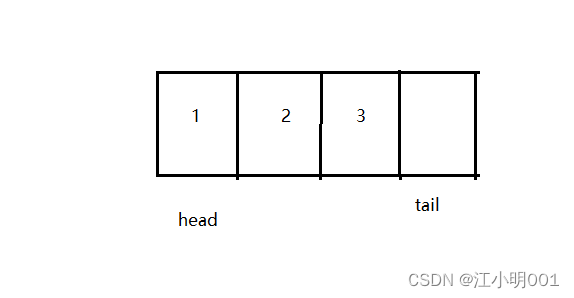
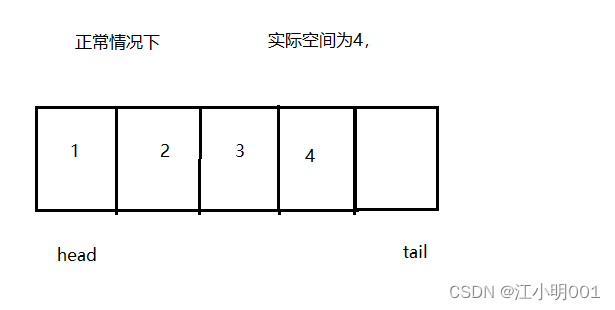
如果是数组的话，我们需要定义三个变量head，tail和k，k是确定队列的空间大小，

假设k=4；

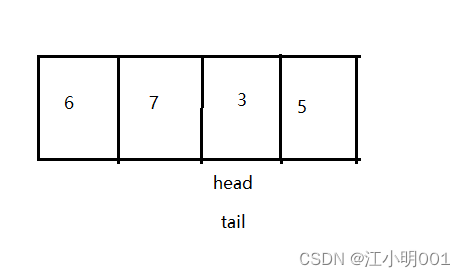
初始化的时候还是一样的head和tail都是0，插入数据插入到tail的位置然后tail++；删除的时候head++；当tail位置如上图形式，在插入数据时，tail要++，怎么回绕到开头的位置呢？其实很简单只需要%一下，先++在%k就回到了开头的位置了，

那什么时候为空什么时候为满呢？

1.为空时head==tail

2.为满时head还是==tail，

这时是不是矛盾了，所以这种方案行不通！

如何解决这个问题呢？

第一种，在增加一个size变量当size=k的时候为满，

第二种，额外开空间

head==tial为空，tail的下一个是head就为满，（tial+1）%（k+1）=head

（tial+1）%（k+1）=head都满足所有判满的情形，也很好的区分开了判空和满的问题，

空和满的问题解决了，那么就是去队头和队尾的数据了

队头很好取，队头就是head，队尾是一个难点

队尾的数据是tail-1的位置

分析：

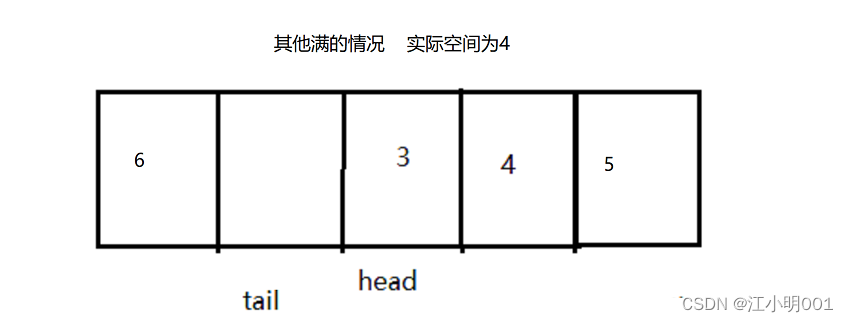
1.当tial在2~最后一个空间之间任意一个空间时队尾的数据就是tial-1，

2.如果tial在第一个的位置时，此时tial=0，tial-1=-1，队尾的数据是最后一空间，最后一个空间的下标为4，所以我们的问题是怎样让tial=4，是不是让tial直接+k（4）就可以了，此时我们可以这样去判断

if(tial>0&&tial