1.动手学习深度学习课程安排及深度学习数学基础

视频资源B站：动手学习深度学习——李沐

目录

• 目标
• 内容
• 将学到什么
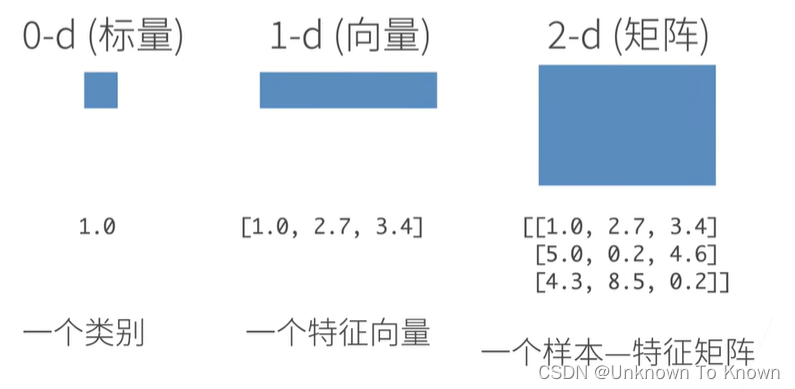
• 1.N维数组样例
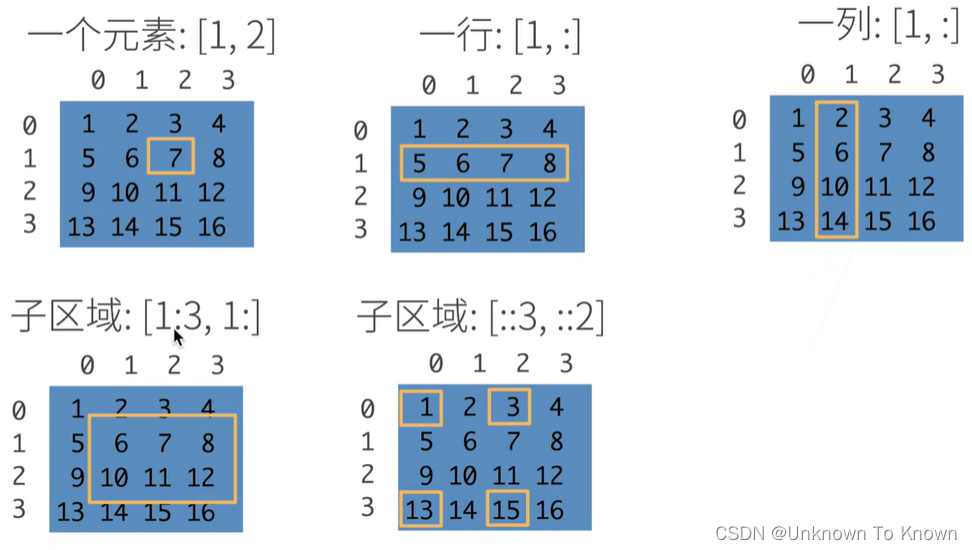
• 2.访问2维数组元素
• 3.数据操作
• 4.线性代数
• 5.矩阵计算
• 6.自动求导

  目标

  • 介绍深度学习景点和最新模型
    • LeNet AlexNet VGG ResNet LSTM BERT…
    • 机器学习基础
      • 损失函数，目标函数，过拟合，优化
      • 实践
        • 使用pytorch实现介绍的知识点
        • 在真实数据上体验算法效果

          内容

          • 深度学习基础——线性神经网络，多层感知机
          • 卷积神经网络——LeNet，AlexNet，VGG，Inception，ResNet
          • 循环神经网络——RNN，GRU，LSTM，seq2seq
          • 注意力机制——Attention，Transformer
          • 优化算法——SGD，Momentum，Adam
          • 高性能计算——并行，多GPU，分布式
          • 计算机视觉——目标检测，语义分割
          • 自然语言处理——词嵌入，BERT

            将学到什么

            • What
              • 深度学习里有那些技术
              • How
                • 如何实现和调参
                • Why
                  • 背后的原因（直觉，数学）

                    1.N维数组样例

                    N维数组是机器学习和神经网络的主要数据结构

                    

                    

                    2.访问2维数组元素

                    

                    3.数据操作

                    ​ 首先，我们导入torch，注意，虽然它被称为pytorch，但我们应该导入torch而不是pytorch

                    import torch
                    #张量表示一个数值组成的数组，这个数组可能有多个纬度
                    x = torch.arange(12)#输出：1 2 3 ...12
                    x.shape#输出：torch.Size([12])
                    x.numel#输出：12
                    #要改变一个张量的形状而不改变元素数量和元素值，我们可以调用reshape函数
                    x = x.reshape(3,4)
                    #输出：
                    。。。。。。不再过多的描述
                    

                    4.线性代数

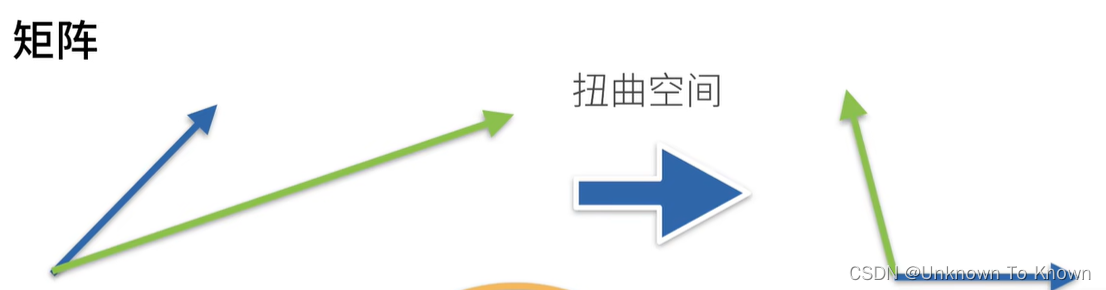
                    矩阵相当于一个扭曲空间，把下图中的蓝线和绿线，扭曲到不同方向和长度

                    

                    5.矩阵计算

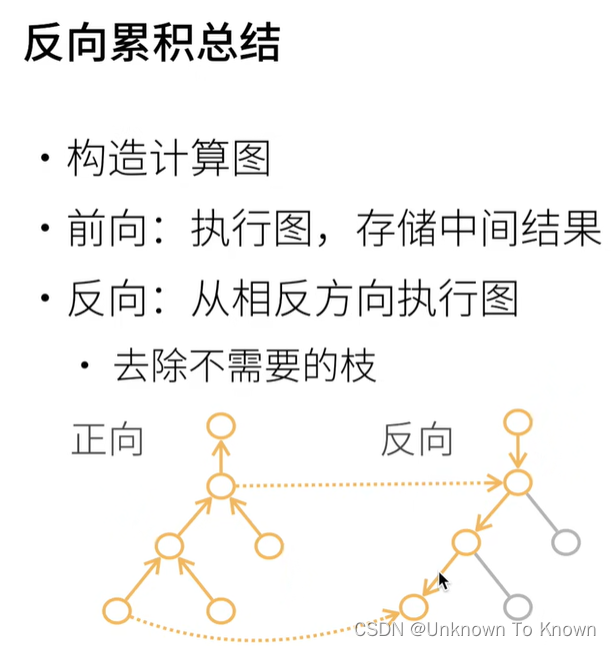
                    6.自动求导

                    

                    

                    

                    复杂度：

                    • 计算复杂度：O(n)，n为操作字个数
                      • 通常正向和反向的代价类似
                      • 内存复杂度：O(n)，因为需要存储正向的所有中间结果
                      • 跟正向累积对比
                        • O(n)计算复杂度用来计算一个变量的梯度
                        • O(1)内存复杂度