机器学习每周挑战——二手车车辆信息&交易售价数据
温馨提示:这篇文章已超过370天没有更新,请注意相关的内容是否还可用!
这是数据集的截图
目录
背景描述
数据说明
车型对照:
燃料类型对照:
老规矩,第一步先导入用到的库
第二步,读入数据:
第三步,数据预处理
第四步:对数据的分析
第五步:模型建立前的准备工作
第六步:多元线性回归模型的建立
第七步:随机森林模型的建立
问题:
背景描述
本数据爬取自印度最大的二手车交易平台 CARS24,包含 8000+ 该平台上交易车辆的关键评估信息。
CARS24 成立于 2015 年,总部位于印度古尔冈,是一个在印度、澳大利亚、泰国和阿联酋运营的二手车交易平台,为用户提供一站式二手车交易服务,包括车辆评估、交易、融资、保险等。CARS24 已成为印度最大的二手车交易平台之一,在印度拥有超过 1000 家线下门店。
数据说明
| 字段 | 说明 |
|---|---|
| Car Name | 汽车品牌或汽车型号 |
| Distance | 行驶里程 (单位:公里) |
| Year Bought | 购车年份 |
| Previous Owners | 前任车主数量 |
| Location | 车管所所在地 |
| Transmission | 变速箱类型 (automatic自动 或 manua手动) |
| Car Type | 车型 |
| Fuel | 燃料类型 (汽油、柴油、CNG 等) |
| Price | 价格 |
-
车型对照:
英文 中文 sedan 轿车 SUV SUV hatchback 两厢车 luxury SUV 豪华SUV luxury sedan 豪华轿车 -
燃料类型对照:
英文 中文 petrol 汽油 diesel 柴油 CNG 压缩天然气 other 其他 老规矩,第一步先导入用到的库
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt from sklearn.metrics import confusion_matrix import statsmodels.api as sm from statsmodels.formula.api import ols from sklearn.preprocessing import StandardScaler,LabelEncoder,OneHotEncoder from statsmodels.stats.outliers_influence import variance_inflation_factor from sklearn.model_selection import train_test_split,cross_val_score from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error,r2_score,classification_report import scipy.stats as stats from statsmodels.stats.stattools import durbin_watson from statsmodels.stats.diagnostic import het_breuschpagan from scipy.stats import kstest from sklearn.ensemble import RandomForestRegressor from hyperopt import fmin, tpe, hp,STATUS_OK
第二步,读入数据:
data = pd.read_csv('cars_24.csv') pd.set_option('display.max_columns',1000) pd.set_option('display.max_rows',1000) plt.rcParams['axes.unicode_minus'] = False plt.rcParams['font.family'] = ['Microsoft YaHei']第三步,数据预处理
print(data.info()) # 从这里我们可以看出Location Year Car Name 三列数据有确实值,由于位置信息无法填充,因此我选择将缺失值删除 data.dropna(inplace=True) for col in data.columns: print(col) print(data[col].unique()) print('/'*20) # 通过上面的循环我们可以了解到所有列的唯一值,排除Index Distance Price这些连续值,我们可以看出其他特征列都有那些值 # 删除包含22-BH的行,因为在印度的车辆注册号码中,BH通常不是一个标准的州或联邦领地代码,这可能是数据有误,这里直接删除 data = data[data['Location'] != '22-BH'] # 由于Car Name名字太多,因此我们只提取品牌,即,第一个空格前面的 data['Brand'] = data['Car Name'].apply(lambda x: x.split()[0]) # 有了Brand后,我们将原先的Car Name这一列删除 data = data.drop('Car Name',axis=1) data['Location'] = data['Location'].apply(lambda x:x[:2]) # print(data['Location'].unique()) # 如果前面我们没发现22-BH这种异常值,我们从这里发现后,我们也可以将其删除 # data['Location'] = [x for x in data['Location'] if x!=22] # 标签这一列对于我们来说也没有用,因此我们也将其删除 data.drop('Index',axis=1,inplace=True) # 将年份转换为整数 data['Year'] = data['Year'].astype(int) # 我们对预处理后的数据进行复制,以便于我们后续对数据进行建模 new_data = data.copy()第四步:对数据的分析
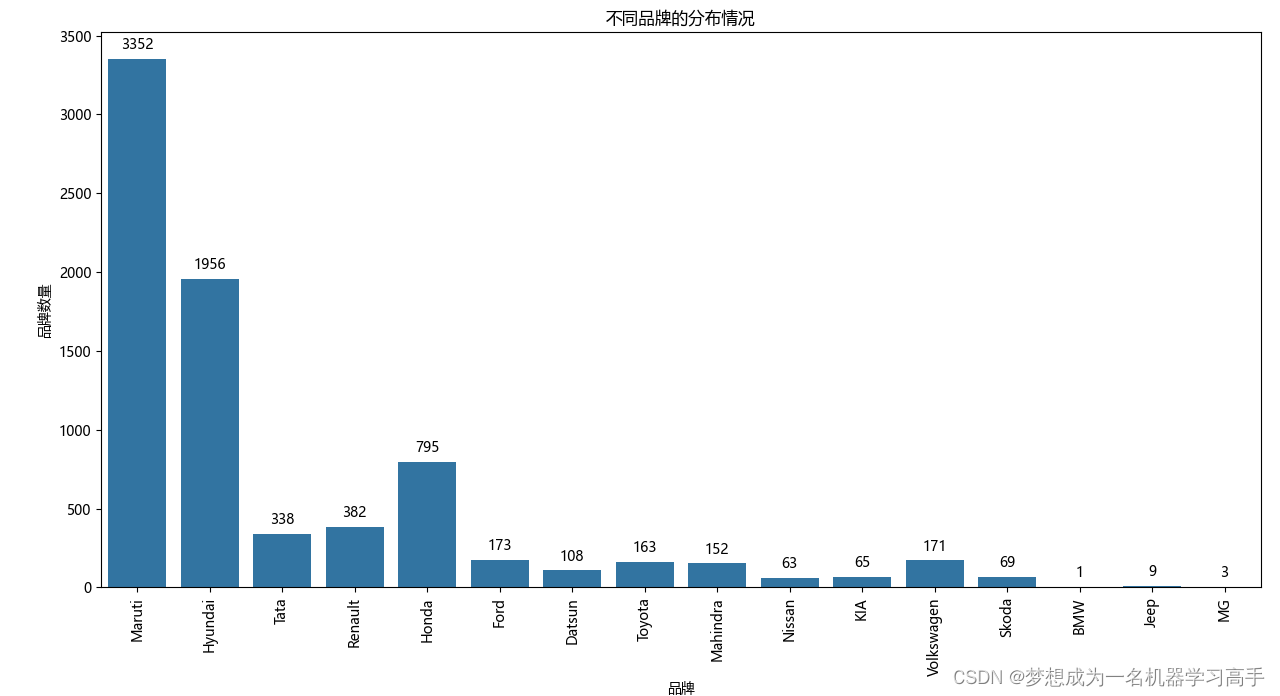
# 接下来我们对数据进行分析,通过图表来观察他们各个特征之间的关联 plt.figure(figsize=(10,8)) ax = sns.countplot(x='Brand',data=data) plt.title('不同品牌的分布情况') plt.xlabel('品牌') plt.ylabel('品牌数量') plt.xticks(rotation=90) plt.tight_layout() for p in ax.patches: ax.annotate(format(p.get_height(), '.0f'), (p.get_x() + p.get_width() / 2., p.get_height()), ha = 'center', va = 'center', xytext = (0, 10), textcoords = 'offset points') plt.show()所有二手车品牌中,马鲁蒂(Maruti)和现代(Hyundai)的数量是最多的,马鲁蒂是印度的一个知名品牌,所以占比也是最大的
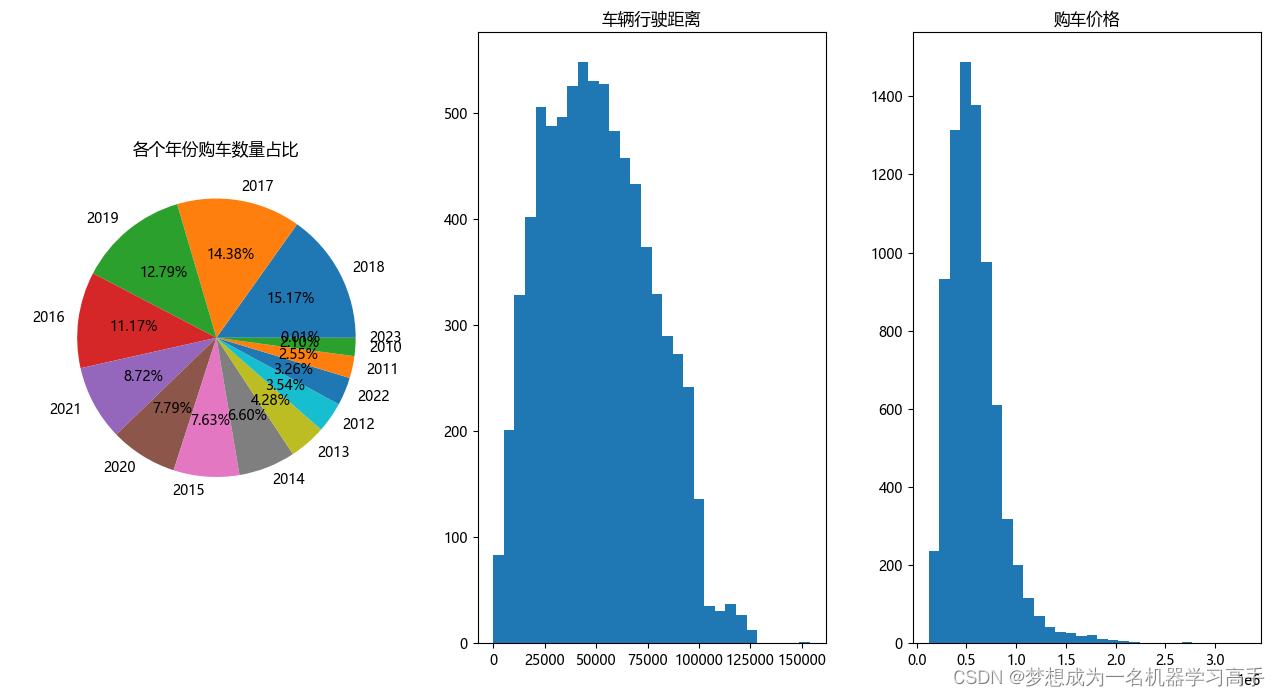
fig,ax = plt.subplots(1,3,figsize=(10,8)) count_year = data['Year'].value_counts() label = count_year.index # print(label) ax[0].pie(count_year,labels=label,autopct='%.2f%%') ax[0].set_title('各个年份购车数量占比') ax[1].hist(data['Distance'],bins=30) ax[1].set_title('车辆行驶距离') ax[2].hist(data['Price'],bins=30) ax[2].set_title('购车价格') plt.tight_layout() plt.show()总结:数据集中的车辆大多数是17,18年购买的,有较短的行驶距离,且价格相对较低
fig,ax = plt.subplots(2,2,figsize=(10,8)) owner_plot = sns.countplot(ax=ax[0,0],x='Owner',data=data) ax[0,0].set_title('前任车主特征分布图') ax[0,0].set_xlabel('前任车主') ax[0,0].set_ylabel('总数') for x in owner_plot.patches: owner_plot.annotate(format(x.get_height(),'.0f'), (x.get_x()+x.get_width()/2,x.get_height()), ha='center',va='center', xytext=(0,10), textcoords='offset points') fuel_plot = sns.countplot(ax=ax[0,1],x='Fuel',data=data) ax[0,1].set_title('燃料类型特征分布图') ax[0,1].set_xlabel('燃料类型') ax[0,1].set_ylabel('总数') for x in fuel_plot.patches: fuel_plot.annotate(format(x.get_height(),'.0f'), (x.get_x()+x.get_width()/2,x.get_height()), ha='center',va='center', xytext=(0,10), textcoords='offset points') drive_plot = sns.countplot(ax=ax[1,0],x='Drive',data=data) ax[1,0].set_title('变速器类型特征分布图') ax[1,0].set_xlabel('变速器类型') ax[1,0].set_ylabel('总数') for x in drive_plot.patches: drive_plot.annotate(format(x.get_height(),'.0f'), (x.get_x()+x.get_width()/2,x.get_height()), ha='center',va='center', xytext=(0,10), textcoords='offset points') type_plot = sns.countplot(ax=ax[1,1],x='Type',data=data) ax[1,1].set_title('车辆类型特征分布图') ax[1,1].set_xlabel('车辆类型') ax[1,1].set_ylabel('总数') for x in type_plot.patches: type_plot.annotate(format(x.get_height(),'.0f'), (x.get_x()+x.get_width()/2,x.get_height()), ha='center',va='center', xytext=(0,10), textcoords='offset points') plt.tight_layout() plt.show()1.大多数车都是一手车(只有一个前任车主)。
2.大多数车都是使用汽油(Petrol),然后就是柴油(Diesel),天然气(CNG)和液化石油气(LPG)作为燃料类型的车辆数量相对较少。
3.手动挡(Manual)车辆数量大于自动挡(Automatic)车辆数量。
4.掀背车(HatchBack)是最常见的车型,其次是轿车(Sedan)和SUV,豪华SUV(Lux_SUV)和豪华轿车(Lux_sedan)的数量相对较少。
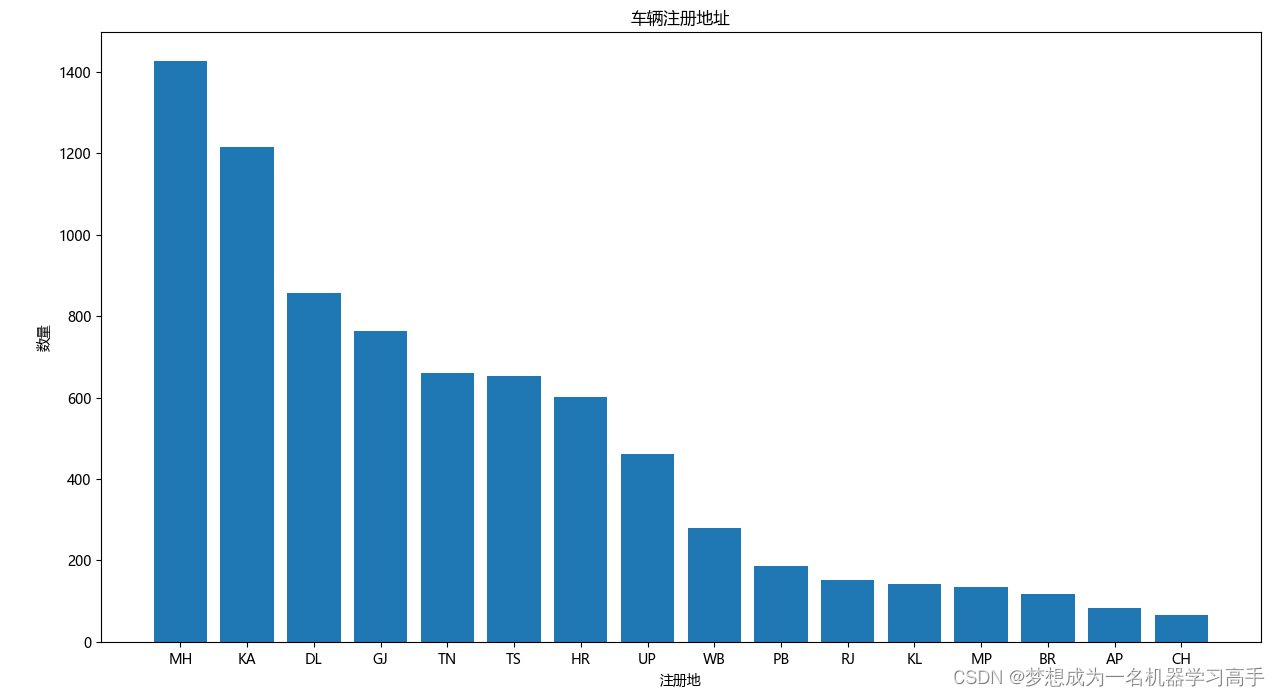
plt.figure(figsize=(10,8)) registration = data['Location'].value_counts().reset_index() # print(registration) plt.bar(registration['Location'],registration['count']) plt.title('车辆注册地址') plt.xlabel('注册地') plt.ylabel('数量') plt.tight_layout() plt.show()MH和KA有较多的车辆注册,CH、KL、RJ、BR、AP、MP有较少的车辆注册,较少的注册数量可能表明在某些州二手车市场的规模较小。
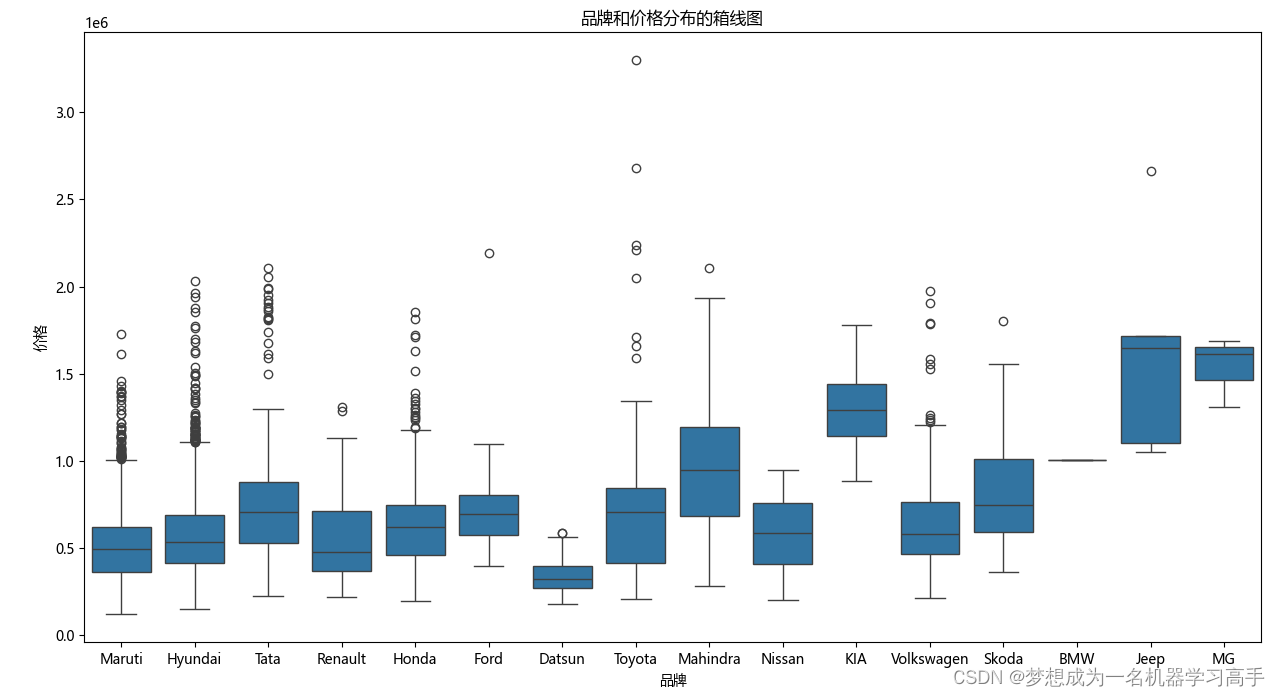
plt.figure(figsize=(10,8)) sns.boxplot(x='Brand',y='Price',data=data) plt.title('品牌和价格分布的箱线图') plt.xlabel('品牌') plt.ylabel('价格') plt.tight_layout() plt.show()可以看到,不同品牌之间的汽车价格有明显差异,达特桑(Datsun)、马鲁蒂(Maruti)价格普遍比较低,吉普(Jeep)、名爵(MG) 价格普遍偏高,当然,这也可能是因为数据样本少导致的,但是从整体上看,可以认为不同品牌之间的汽车价格有明显差异。
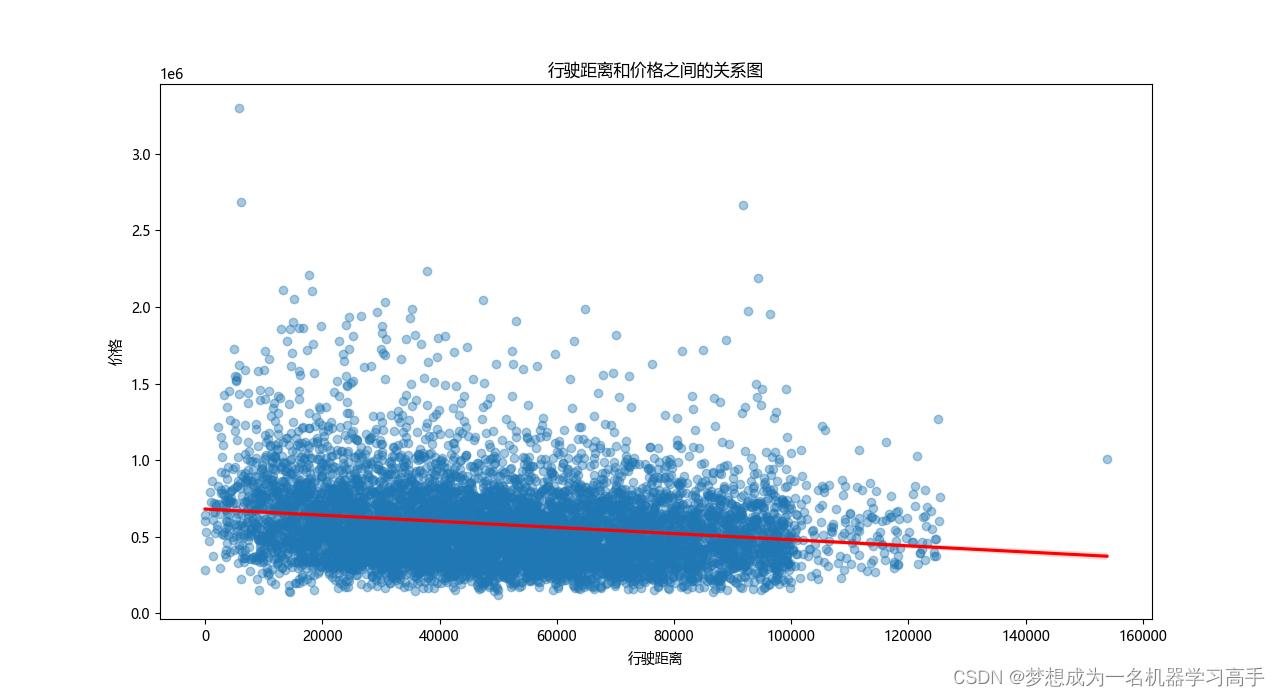
plt.figure(figsize=(10,8)) sns.regplot(x='Distance',y='Price',data=data,scatter_kws={'alpha':0.4},line_kws={'color':'red'}) plt.title('行驶距离和价格之间的关系图') plt.xlabel('行驶距离') plt.ylabel('价格') plt.show()行驶距离和价格之间没有明显的线性关系,虽然价格的整体趋势似乎随行驶距离的增加而下降,但数据点较为分散
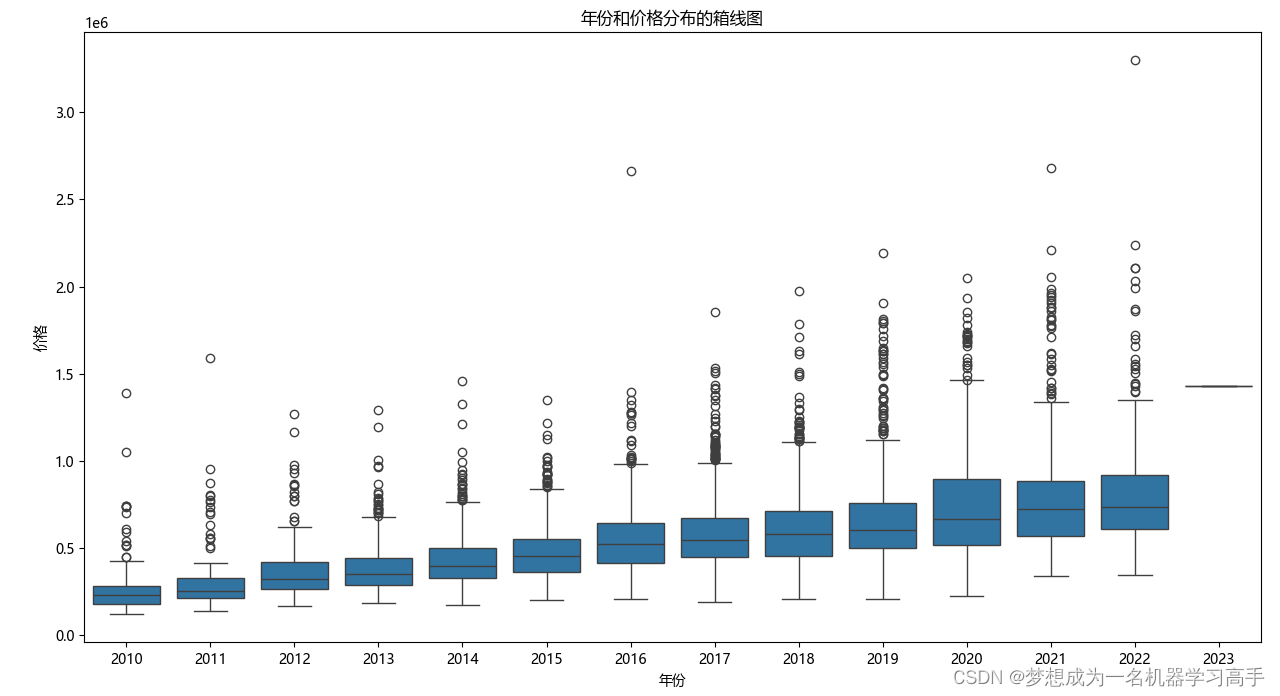
plt.figure(figsize=(10,8)) sns.boxplot(x='Year',y='Price',data=data) plt.title('年份和价格分布的箱线图') plt.xlabel('年份') plt.ylabel('价格') plt.tight_layout() plt.show()购买年份是影响二手车价格的一个重要因素,不同年份的车辆价格分布有显著差异,随着购买年份越近,车辆价格也越高。
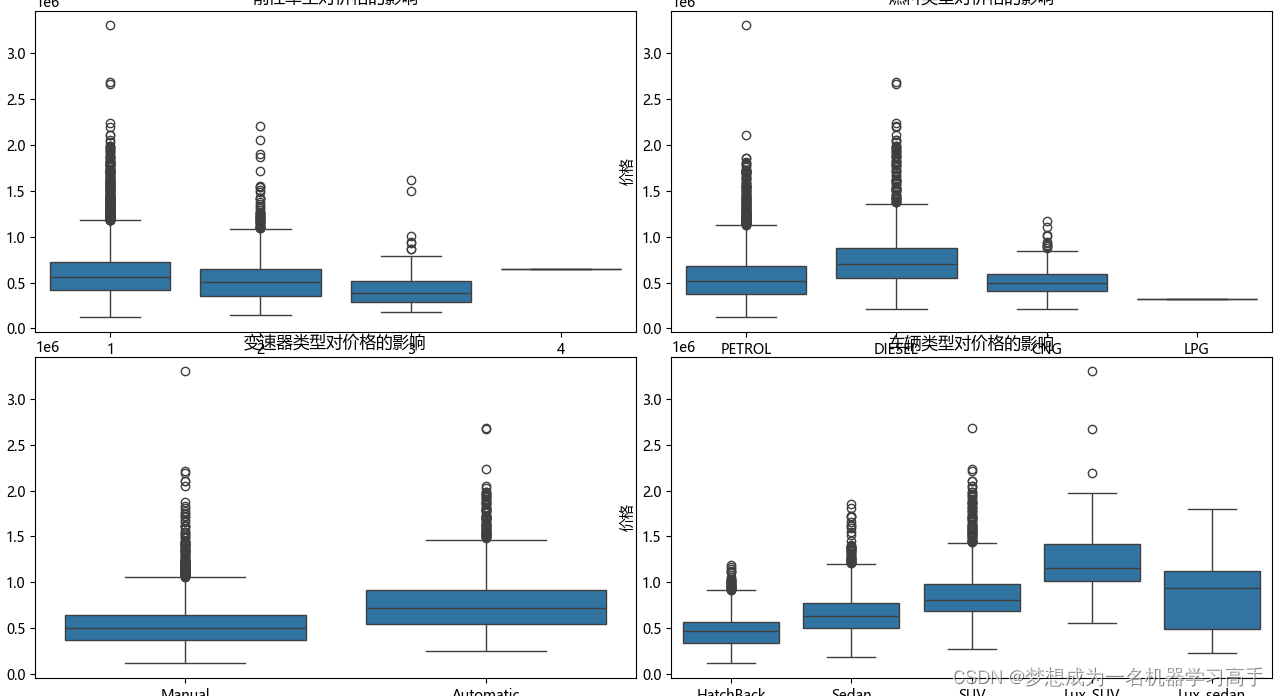
fig, axes = plt.subplots(2, 2, figsize=(24, 24)) # 前任车主的数量对价格的影响 sns.boxplot(ax=axes[0, 0], x='Owner', y='Price', data=data) axes[0, 0].set_title('前任车主对价格的影响') axes[0, 0].set_xlabel('前任车主的数量') axes[0, 0].set_ylabel('价格') # 燃料类型对价格的影响 sns.boxplot(ax=axes[0, 1], x='Fuel', y='Price', data=data) axes[0, 1].set_title('燃料类型对价格的影响') axes[0, 1].set_xlabel('燃料类型') axes[0, 1].set_ylabel('价格') # 变速器类型对价格的影响 sns.boxplot(ax=axes[1, 0], x='Drive', y='Price', data=data) axes[1, 0].set_title('变速器类型对价格的影响') axes[1, 0].set_xlabel('变速器类型') axes[1, 0].set_ylabel('价格') # 车辆类型对价格的影响 sns.boxplot(ax=axes[1, 1], x='Type', y='Price', data=data) axes[1, 1].set_title('车辆类型对价格的影响') axes[1, 1].set_xlabel('车辆类型') axes[1, 1].set_ylabel('价格') plt.tight_layout() plt.show()1.前任车主越多,价格越低,至于4手车因为数据样本只有一个,导致价格偏高,但是仍然可以认为前任车主的数量与价格有显著关系。
2.柴油车的价格要高于其他三种类型的汽车,可以认为不同燃料类型之间的汽车价格有明显差异。
3.整体上,自动挡的车价格要高于手动挡的车。
4.豪华版的汽车价格整体上更贵,其次是SUV的价格高于轿车(Sedan),高于掀背车(HatchBack),也就是两厢车,因此可以认为不同类型之间的汽车价格有明显差异。
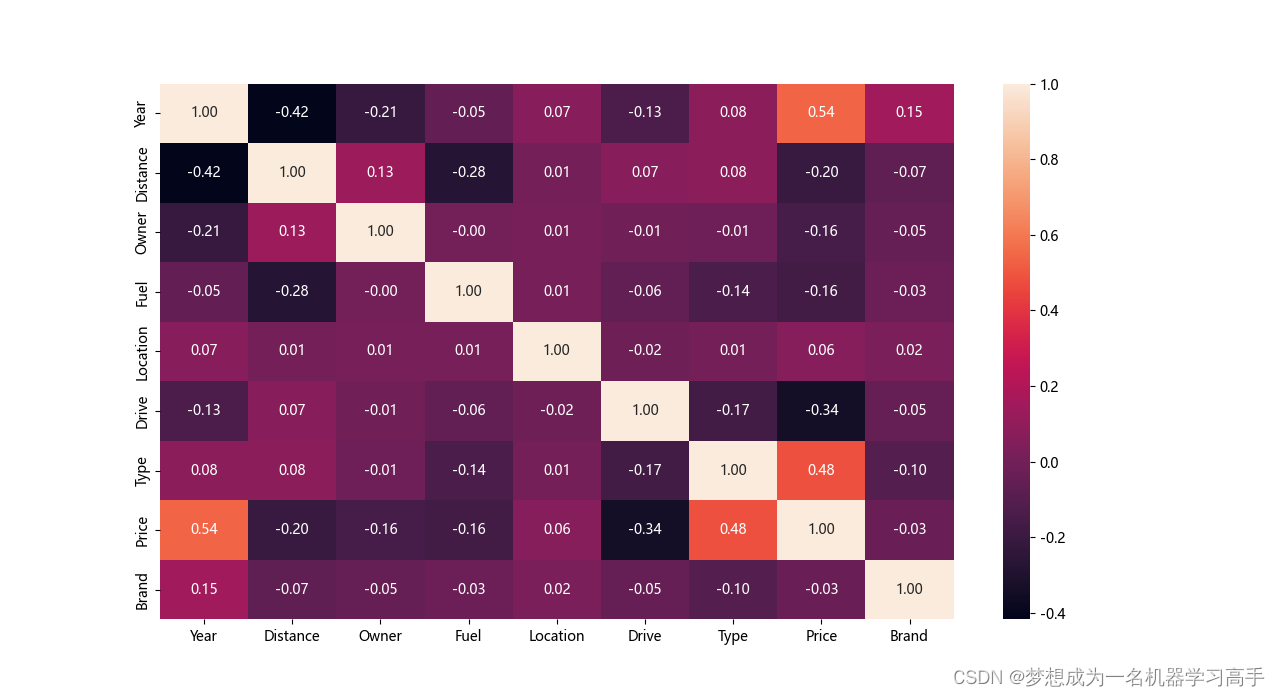
# 对于价格的影响因素我们可以通过斯皮尔曼来确定 print(data.info()) le = LabelEncoder() for col in data.columns: data[col] = le.fit_transform(data[col]) corr = data.corr(method='spearman') plt.figure(figsize=(10,8)) sns.heatmap(corr,color='red',annot=True,fmt='.2f') plt.show()通过热力图我们可以发现年份,变速器类型,和车辆类型对价格的影响较高。
第五步:模型建立前的准备工作
new_data = pd.get_dummies(new_data,columns=['Brand','Fuel','Location','Type','Drive'],dtype=int) # print(new_data.info()) # 对车辆行驶距离进行对数变化处理,因为行驶距离成右偏分布,对数变化可以使得数据更接近正态分布,而且缩小极端值的影响。 new_data['Log_Distance'] = np.log(data['Distance']+1) # 最后,由于部分特征数据跨度较大,因此我们对数据进行标准化 scaler = StandardScaler() features_to_scale = ['Year', 'Log_Distance', 'Owner'] new_data[features_to_scale] = scaler.fit_transform(new_data[features_to_scale]) # 由于我们前面对距离这一列进行对数化操作后,将其重新写入数据中,因此我们将原先的数据列删除 new_data.drop(['Distance'], axis=1, inplace=True) df = new_data.drop('Price',axis=1) df = sm.add_constant(df) # 计算VIF值 vif_data = pd.DataFrame() vif_data['feature'] = df.columns vif_data['VIF'] = [variance_inflation_factor(df.values,i) for i in range(df.shape[1])] # print(vif_data) # 独热编码后又导致了无穷大的多重共线性,这里需要进行处理,直接删除独热编码产生的一个类别(建议选择数量最多的那个), # 这样删除的好处是,当其他类型都为0的时候,实际上表示了这个被删除的特征。 # for col in df.columns: # count = df[col].value_counts() # print(count) # 删除一些独热编码新增的列 new_data.drop(['Brand_Maruti','Fuel_CNG','Location_MH','Type_HatchBack'], axis=1,inplace=True) df = new_data.drop('Price',axis=1) df = sm.add_constant(df) # 计算VIF值,一般来说VIF大于10,这样我们会认为各个特征之间相关性较高,VIF小于5,我们认为各个特征之间相关性较小 vif_data = pd.DataFrame() vif_data['feature'] = df.columns vif_data['VIF'] = [variance_inflation_factor(df.values,i) for i in range(df.shape[1])] # print(vif_data)这里我们可以对比处理之后的VIF值
原先的
feature
VIF
修改后
feature
VIF
0
const
0.000000e+00
0
const
0.000000
1
Year
1.538487e+00
1
Year
1.539060
2
Owner
1.075933e+00
2
Owner
1.076317
3
Brand_BMW
inf
3
Brand_BMW
1.038786
4
Brand_Datsun
3.657790e+10
4
Brand_Datsun
1.039203
5
Brand_Ford
1.306448e+10
5
Brand_Ford
1.220622
6
Brand_Honda
5.115576e+10
6
Brand_Honda
1.306347
7
Brand_Hyundai
2.004020e+09
7
Brand_Hyundai
1.208989
8
Brand_Jeep
1.508666e+09
8
Brand_Jeep
1.181273
9
Brand_KIA
1.197766e+12
9
Brand_KIA
1.107366
10
Brand_MG
9.025250e+12
10
Brand_MG
1.006706
11
Brand_Mahindra
6.519869e+11
11
Brand_Mahindra
1.541723
12
Brand_Maruti
4.401194e+07
12
Brand_Nissan
1.039784
13
Brand_Nissan
2.334987e+08
13
Brand_Renault
1.137255
14
Brand_Renault
5.922232e+09
14
Brand_Skoda
1.072001
15
Brand_Skoda
1.450388e+11
15
Brand_Tata
1.140520
16
Brand_Tata
7.876965e+09
16
Brand_Toyota
1.194287
17
Brand_Toyota
1.386027e+09
17
Brand_Volkswagen
1.057490
18
Brand_Volkswagen
1.412468e+09
18
Fuel_DIESEL
3.147239
19
Fuel_CNG
2.854194e+05
19
Fuel_LPG
1.015113
20
Fuel_DIESEL
6.822078e+04
20
Fuel_PETROL
2.926265
21
Fuel_LPG
inf
21
Location_AP
1.086004
22
Fuel_PETROL
7.304430e+04
22
Location_BR
1.078538
23
Location_AP
3.756073e+08
23
Location_CH
1.067019
24
Location_BR
3.563682e+08
24
Location_DL
1.447625
25
Location_CH
2.543173e+08
25
Location_GJ
1.431759
26
Location_DL
5.847216e+06
26
Location_HR
1.334937
27
Location_GJ
1.088085e+05
27
Location_KA
1.638158
28
Location_HR
1.314777e+05
28
Location_KL
1.097616
29
Location_KA
1.106656e+05
29
Location_MP
1.087806
30
Location_KL
2.893677e+08
30
Location_PB
1.134487
31
Location_MH
1.778885e+04
31
Location_RJ
1.103258
32
Location_MP
1.712941e+08
32
Location_TN
1.402470
33
Location_PB
1.165631e+07
33
Location_TS
1.417552
34
Location_RJ
7.345066e+08
34
Location_UP
1.282728
35
Location_TN
2.105363e+04
35
Location_WB
1.174599
36
Location_TS
2.822998e+06
36
Type_Lux_SUV
1.627484
37
Location_UP
4.673710e+04
37
Type_Lux_sedan
1.207469
38
Location_WB
2.755977e+05
38
Type_SUV
1.697632
39
Type_HatchBack
5.012798e+03
39
Type_Sedan
1.402544
40
Type_Lux_SUV
5.605885e+09
40
Drive_Automatic
inf
41
Type_Lux_sedan
1.691652e+09
41
Drive_Manual
inf
42
Type_SUV
3.487443e+05
42
Log_Distance
1.348290
43
Type_Sedan
3.064002e+05
44
Drive_Automatic
7.560662e+04
45
Drive_Manual
1.163354e+04
46
Log_Distance
1.346594e+00
可以发现,删除了那几列后,除了常数项的方差膨胀因子(VIF)>10,其他特征均在1-4之间,可以认为这个数据特征不存在多重共线性,因此可以使用多元线性回归模型。
第六步:多元线性回归模型的建立
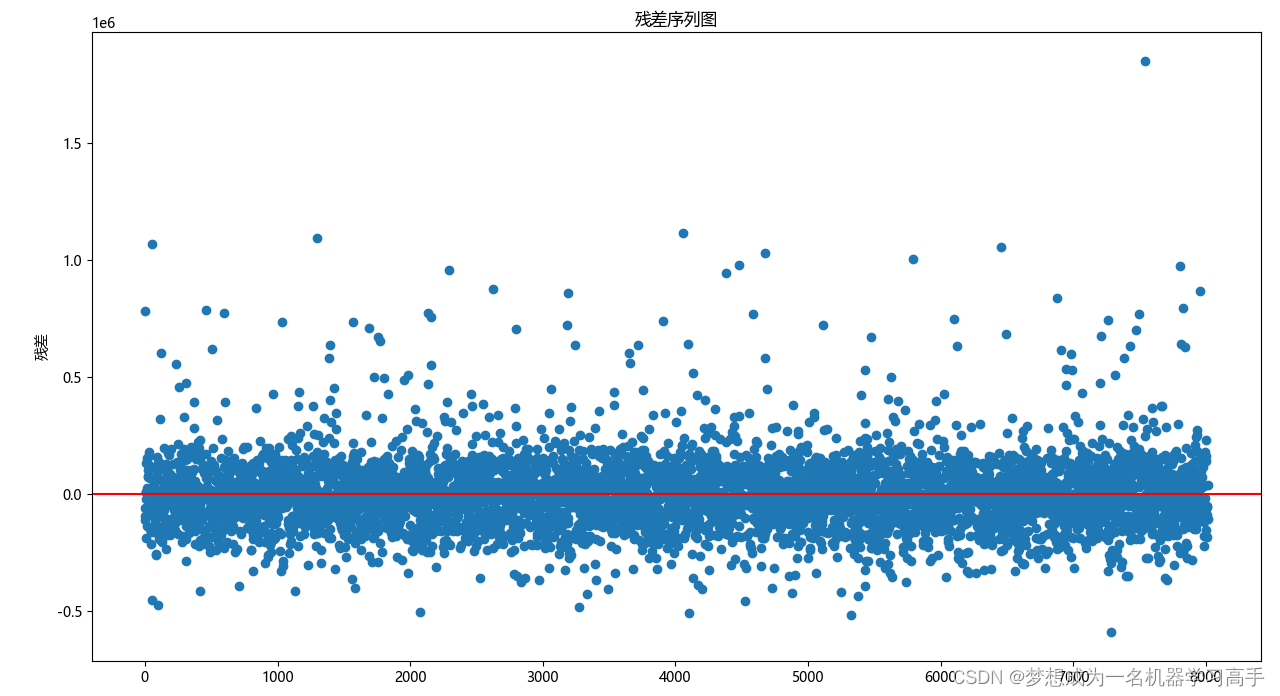
# 接下来我们开始建立模型 X = new_data.drop('Price',axis=1) y = new_data['Price'] # 对X,y进行赋值后,我们对数据进行划分 X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=42) # 创建模型 Re = LinearRegression() Re.fit(X_train,y_train) # 对模型进行训练后,我们需要对残差的正态性分布进行验证,否则多元线性回归模型的预测结果会不准确 pred_y_train = Re.predict(X_train) residuals = y_train-pred_y_train # print(len(residuals)) # 绘制残差序列图 plt.figure(figsize=(10,8)) # sns.regplot(x=np.arange(len(residuals)),y=residuals,scatter_kws={'alpha':0.4},line_kws={'color':'yellow'}) plt.plot(residuals,marker='o',linestyle='') plt.title('残差序列图') plt.ylabel('残差') plt.axhline(y=0,color='red',linestyle='-') # plt.tight_layout() # plt.show() # 画出残差图后,我们对残差的独立性进行检验 dw = durbin_watson(residuals) print('DW检验',dw) # 接下来,我们判断残差的正态性性分布,这里我们用到了KS检验 ks_statistic,ks_p_values = kstest((residuals - np.mean(residuals))/np.std(residuals),'norm') print('正态性P值',ks_p_values) # 验证正态性后,我们还需要验证同方差性 df_ = sm.add_constant(X_train) bp_test = het_breuschpagan(residuals,df_) print('同方差P值',bp_test[1])dw的值在2附近,说明残差的独立性,同时可以从p值看出,残差不符合正态性分布和同方差性分布,因此,不可以用多元线性回归来预测
那我们可以对数据进行优化,比如对因变量(y)进行BOX-COX变换,但是我自己变换后发现还是无法满足正态性分布和同方差性
所以,这里我就不对y进行变换了,不用多元线性回归,我们考虑其他回归模型,比如随机森林,神经网络等
第七步:随机森林模型的建立
Rtree = RandomForestRegressor(random_state=42) Rtree.fit(X_train,y_train) y_pred = Rtree.predict(X_test) # class_report = classification_report(y_test,y_pred) # 注意 classification_report 是用于分类变量的评价指标,不能用于连续变量 mse = mean_squared_error(y_test,y_pred) r2 = r2_score(y_test,y_pred) print('均方根误差:',mse) print('R2决定系数',r2)第八步:随机森林模型的优化
# 效果不是很理想,因此我们对随机森林进行优化,这里使用Hyperopt进行优化 def objective(params): Rtree = RandomForestRegressor(**params) score = -np.mean(cross_val_score(Rtree, X_train, y_train, cv=5, scoring='neg_mean_squared_error')) return {'loss': score, 'status': STATUS_OK, 'model': Rtree} # 设定参数空间 space = { 'n_estimators': hp.choice('n_estimators', range(10, 500)), 'max_depth': hp.choice('max_depth', range(1, 50)), 'min_samples_split': hp.choice('min_samples_split', range(2, 100)), 'min_samples_leaf': hp.choice('min_samples_leaf', range(2, 100)), } # 运行优化 best = fmin(fn=objective, space=space, algo=tpe.suggest, max_evals=100) print("Best parameters found: ", best) Rtree = RandomForestRegressor(**best) Rtree.fit(X_train,y_train) y_pred = Rtree.predict(X_test) mse = mean_squared_error(y_test,y_pred) r2 = r2_score(y_test,y_pred) print('均方根误差:',mse) print('R2决定系数',r2)对模型的优化没有没有多大提升,大家可以试着把n_estimators,max_depth等参数适当调大,可能运行时间较长
由于神经网络通常被称为“黑匣子”模型,因为其内部结构复杂,难以直观理解,且代码偏多,因此我会在后续的每周挑战中单独拿出一起来使用神经网络
问题:
这里我发现了一个问题,那就是我使用独热编码时不知道为什么会出现这种情况,但我前面对于人力资源分析这篇文章里面用的就是这个方法,对每一列进行独热编码,删除原先的列,将其经过独热编码的子列加入到数据集。我感觉思路应该没错,有解决思路的可以私聊我,也可以写在评论区。
encode = OneHotEncoder() for col in new_data.columns: if data[col].dtype == object: encode_data = encode.fit_transform(new_data[[col]]) new_data.drop(col, axis=1, inplace=True) encoded_columns = [f"{col}_{i}" for i in range(encode_data.shape[1])] new_data = pd.concat([new_data, pd.DataFrame(encode_data, columns=encoded_columns)], axis=1) Traceback (most recent call last): new_data = pd.concat([new_data, pd.DataFrame(encode_data, columns=encoded_columns)], axis=1) File "D:\pyobject\pythonProject\.venv\lib\site-packages\pandas\core\frame.py", line 867, in __init__ mgr = ndarray_to_mgr( File "D:\pyobject\pythonProject\.venv\lib\site-packages\pandas\core\internals\construction.py", line 336, in ndarray_to_mgr _check_values_indices_shape_match(values, index, columns) File "D:\pyobject\pythonProject\.venv\lib\site-packages\pandas\core\internals\construction.py", line 420, in _check_values_indices_shape_match raise ValueError(f"Shape of passed values is {passed}, indices imply {implied}") ValueError: Shape of passed values is (7800, 1), indices imply (7800, 4)