第3章 3.3 MATLAB中的矩阵（MATLAB入门课程）

讲解视频：可以在bilibili搜索“MATLAB教程新手入门篇——数学建模清风主讲”。

MATLAB教程新手入门篇（数学建模清风主讲，适合零基础同学观看）_哔哩哔哩_bilibili

上一节中介绍了MATLAB中向量的基本操作，本节介绍MATLAB中矩阵的相关知识。因为向量可以看成矩阵的一个特例，所以它们有许多类似的操作。

3.3.1 矩阵的创建方法

在MATLAB中，矩阵的创建方法主要有三种，分别是：直接输入法、函数创建法和导入本地文件中的数据。大家可以打开本节的配套代码：“code_3_3_1”进行学习。

（1）直接输入法

我们先来看直接输入法，直接输入法适用于矩阵中元素数量较少的情况。

输入矩阵时要以中括号“[ ]”作为标识符号，矩阵的所有元素必须都在中括号内。矩阵的同行元素之间用空格或逗号分隔，行与行之间用分号或回车键分隔。

例如：命令a = [1 2 3; 4 5 6]; 可以在工作区创建出变量名为a的矩阵。

（2）函数创建法

MATLAB提供了一些函数，这些函数可以用来生成某些特定的矩阵，我们这里介绍几组最常用到的函数。

第一组函数： zeros、ones和eye。这三个函数分别用来创建全为0的矩阵、全为1的矩阵和单位矩阵。

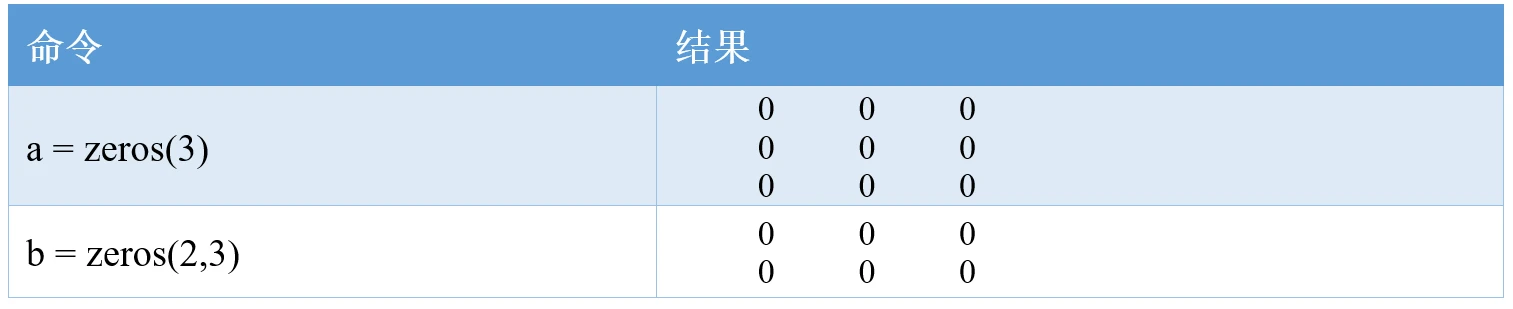
以zeros函数为例，其常见的用法有两种：（1）zeros(n)可以创建一个n行n列全为0的矩阵；（2）zeros(m,n)可以创建一个m行n列全为0的矩阵。

例如：

ones和eye的用法类似，大家可以看配套的讲解视频或者查看MATLAB的帮助文档。

第二组函数： rand、randi和randn。这三个函数分别用来创建均匀分布的随机数、均匀分布的随机整数和标准正态分布的随机数，以后会大量用到，请大家熟记。（数据的分布是概率论里面的知识点，没学过的同学可以搜索关键词自学）

rand函数用来创建区间0和1内均匀分布的随机数，其最常用的方法有两种：（1）rand(n)可以创建一个n行n列的随机数矩阵；（2）rand(m,n)可以创建一个m行n列的随机数矩阵。由rand函数创建的随机数矩阵的每个元素都随机取样自0和1之间的均匀分布。

randi函数用来创建均匀分布的随机整数，其最一般的用法为：randi([imin,imax],m,n)，该命令可创建一个m行n列的随机数矩阵，随机数矩阵中的每个元素都是从区间[imin,imax]内随机抽取的整数。举个例子，假设我们要模拟投掷100次骰子，骰子有6个面，那么我们可以使用randi([1,6],1,100)得到一个长度为100的行向量，向量中的每个元素都是取自1,2,3,4,5,6中的一个整数。另外，如果imin等于1，那么可以简写为randi(imax,m,n)；如果m和n相同，即生成一个n行n列的方阵，那么可以直接写成randi([imin,imax],n)。

randn函数用来创建标准正态分布的随机数，其使用方法和rand函数类似：（1）randn(n)可以创建一个n行n列的随机数矩阵；（2）randn(m,n)可以创建一个m行n列的随机数矩阵。由randn函数创建的随机数矩阵的每个元素都随机取样自标准正态分布。

注意：因为我们生成的是随机数，所以每次运行的结果可能会变化。除了上述这几个函数外，MATLAB还提供了其他一些与随机数生成相关的函数，感兴趣的同学可以在MATLAB官网搜索关键词：随机数。

第三组函数：diag和blkdiag。

diag函数可用来创建对角矩阵或者获取矩阵的对角元素

情况1：如果输入的第一个参数是向量，则表示创建对角矩阵。

    diag(v, k) 将向量v的元素放置在第k条对角线上，其他位置元素为0。

    k=0 表示主对角线，k>0 位于主对角线上方，k