【MATLAB】史上最全的5种数据插值算法全家桶
有意向获取代码,请转文末观看代码获取方式~
大家吃一顿火锅的价格便可以拥有5种数据插值算法,绝对不亏,知识付费是现今时代的趋势,而且都是我精心制作的教程,有问题可随时反馈~也可单独获取某一算法的代码(见每一算法介绍后文)~
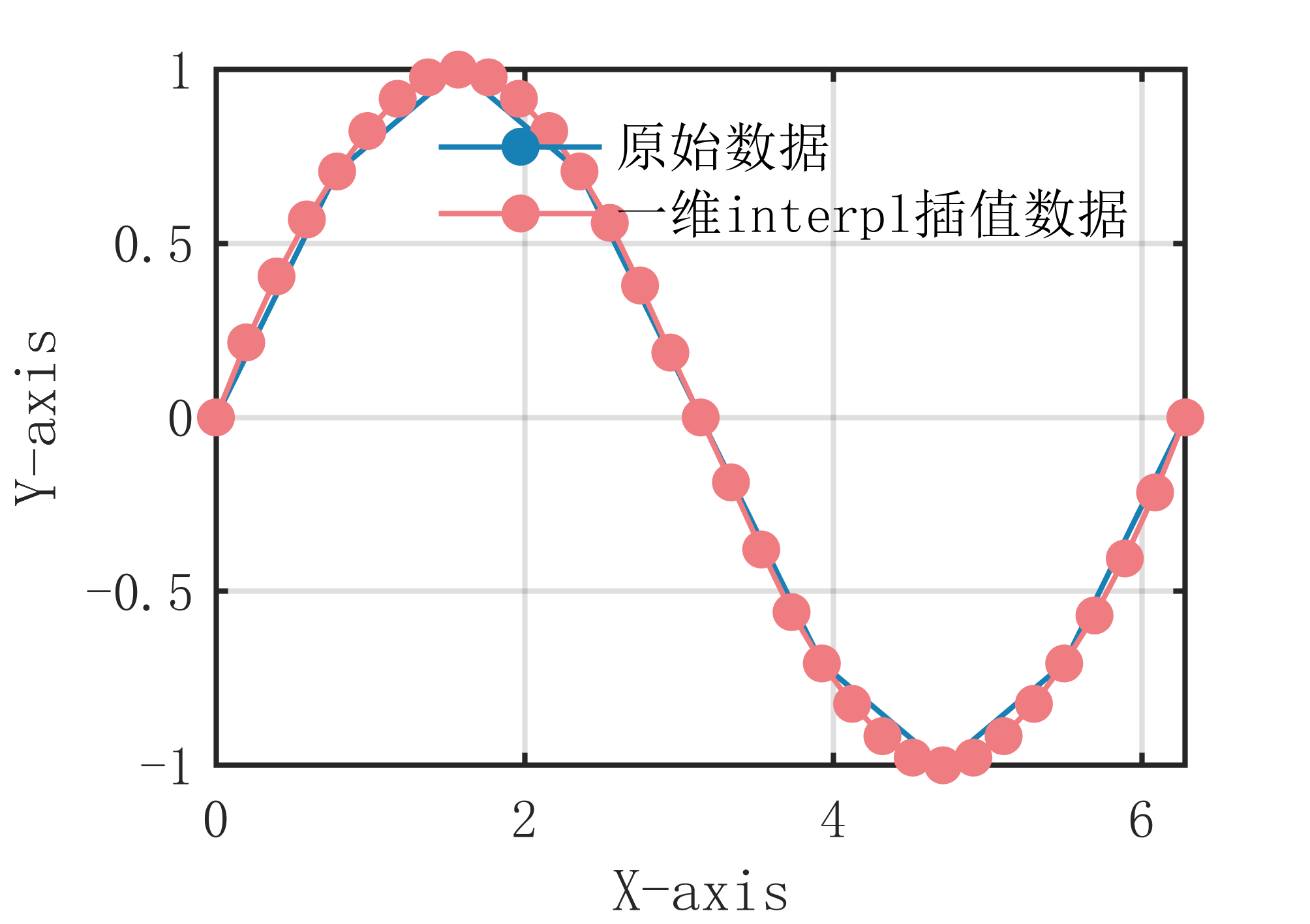
1 【MATLAB】一维interpl插值算法
一维interpl插值算法原理是在已知一系列离散数据点的情况下,通过插值计算得到任意一点的函数值。具体算法步骤如下:
-
输入一组已知的离散数据点 ,其中 是自变量, 是因变量。
-
对数据点按照 值从小到大进行排序。
-
对于给定的待插值点 ,找到插值区间 ,使得 。
-
利用已知点之间的直线作为插值函数,即根据公式 计算出插值点 的函数值 。
-
输出插值点 的函数值 。 一维interpl插值算法的核心思想是在已知数据点之间进行线性插值,通过利用已知点之间的直线来估计未知点的函数值。整个算法过程简单易懂,计算速度快,适用于一些简单的数据插值问题。
插值算法示意图
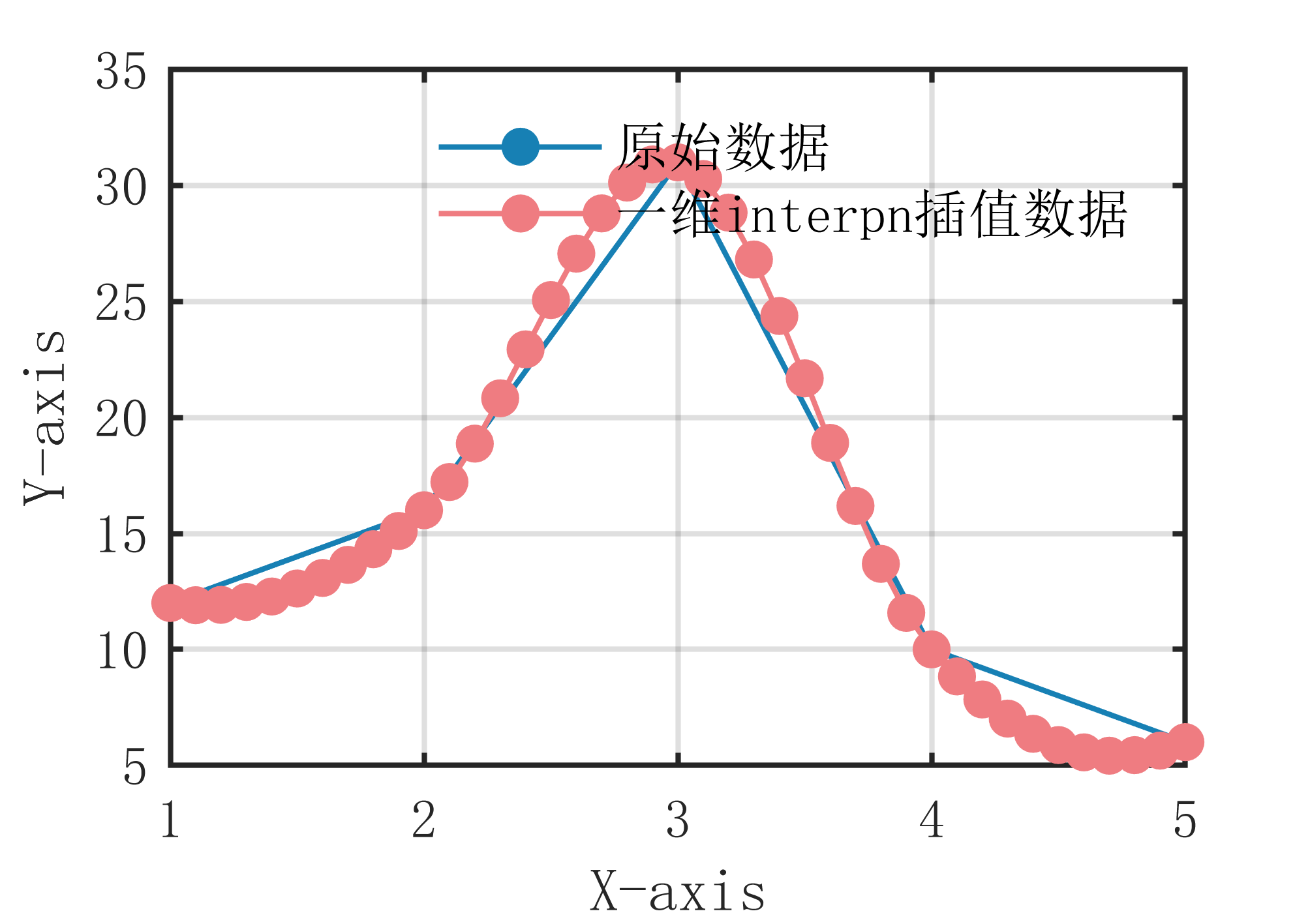
2【MATLAB】一维interpn插值算法
一维interpn插值算法原理是在已知n维数据点的情况下,通过插值计算得到任意一点的函数值。具体算法步骤如下:
-
输入一组已知的n维离散数据点 ,其中 是自变量, 是因变量,,。
-
对数据点按照 值从小到大进行排序。
-
对于给定的待插值点 ,找到插值区间 ,使得 。
-
利用已知点之间的直线作为插值函数,即根据公式 计算出插值点 的函数值 。
-
输出插值点 的函数值 。 一维interpn插值算法的核心思想是在已知n维数据点之间进行线性插值,通过利用已知点之间的直线来估计未知点的函数值。整个算法过程相对于一维interpl插值算法稍微复杂一些,需要考虑多个自变量之间的相互作用,但是它仍然是一种简单易懂,计算速度快的插值方法。当然,如果数据点之间存在非线性关系,需要使用更高阶的插值方法来获得更高的插值精度。
插值算法示意图
3【MATLAB】二维interp2插值算法
二维interp2插值算法原理是在已知二维离散数据点的情况下,通过插值计算得到任意一点的函数值。具体算法步骤如下:
-
输入一组已知的二维离散数据点 ,其中 和 是自变量, 是因变量。
-
对数据点按照 和 值从小到大进行排序。
-
对于给定的待插值点 ,找到插值区间 和 ,使得 ,。
-
利用已知点之间的二维平面作为插值函数,即根据公式 计算出插值点 的函数值 。
-
输出插值点 的函数值 。 二维interp2插值算法的核心思想是在已知二维数据点之间进行二维平面插值,通过利用已知点之间的二维平面来估计未知点的函数值。整个算法过程相对于一维插值算法更加复杂一些,但是它仍然是一种简单易懂,计算速度快的插值方法。当然,如果数据点之间存在非线性关系,需要使用更高阶的插值方法来获得更高的插值精度。
插值算法示意图
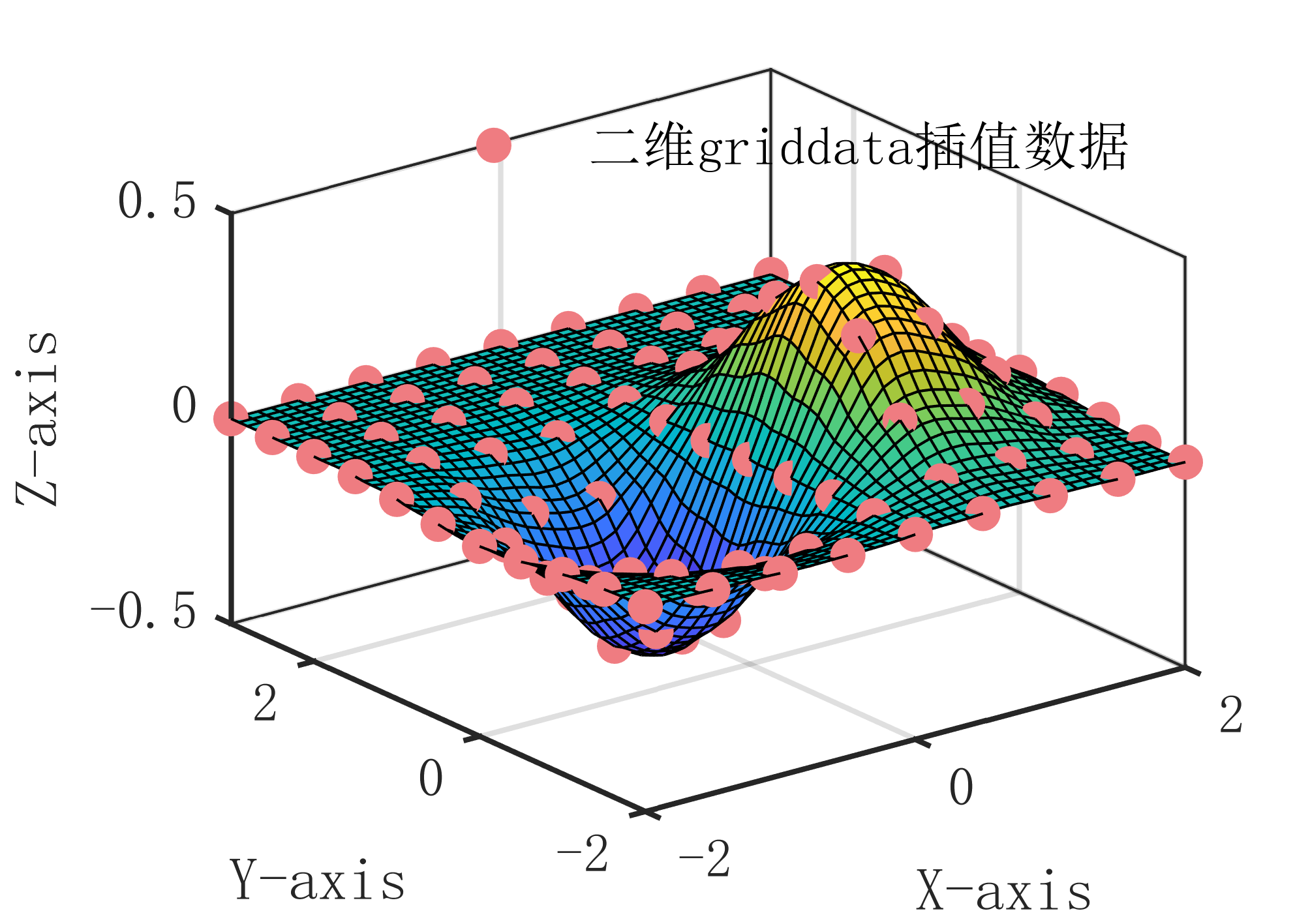
4【MATLAB】二维griddata插值算法
二维griddata插值算法原理是在已知二维离散数据点的情况下,通过插值计算得到任意一点的函数值。具体算法步骤如下:
-
输入一组已知的二维离散数据点 ,其中 和 是自变量, 是因变量。
-
根据已知数据点,在二维平面上生成一个网格,网格点的坐标为 。
-
对于每个网格点 ,根据其周围已知数据点的函数值,计算出其函数值 。这里可以使用不同的插值方法,如线性插值、最近邻插值、三次样条插值等。
-
对于给定的待插值点 ,找到其所在的网格点 。
-
输出网格点 的函数值 。 二维griddata插值算法的核心思想是在已知二维数据点之间生成一个网格,通过利用周围已知数据点的函数值来估计未知点的函数值。相对于interp2插值算法,它的插值精度更高,但计算速度比较慢。同时,它也能够处理不规则的数据点分布,因此在实际应用中具有广泛的应用。
插值算法示意图
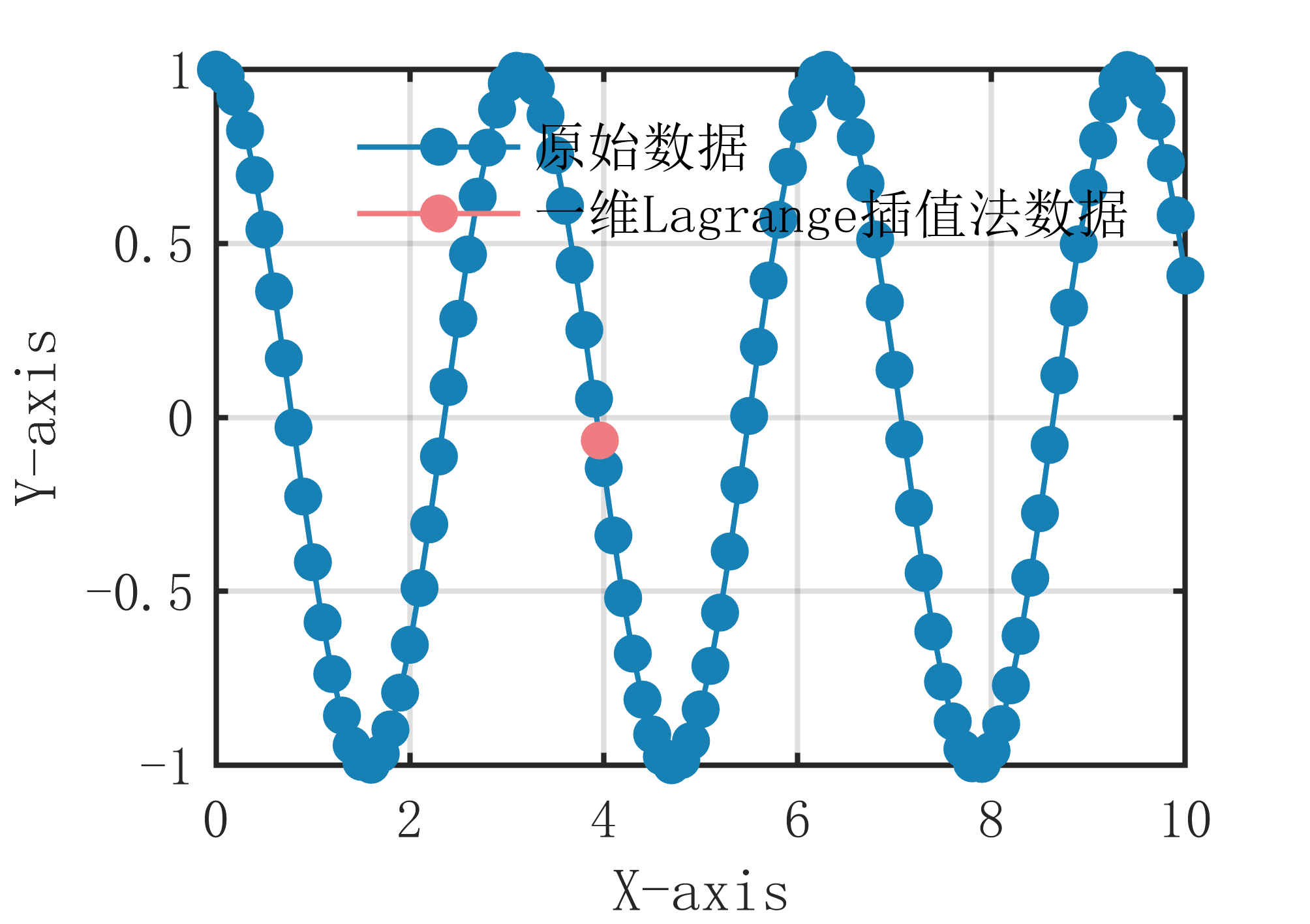
5【MATLAB】一维Lagrange插值算法
一维Lagrange插值算法原理是在已知n个数据点的情况下,通过构造一个n-1次的多项式函数来插值计算任意一点的函数值。具体算法步骤如下:
-
输入一组已知的离散数据点 ,其中 是自变量, 是因变量。
-
构造一个n-1次的多项式函数 ,满足在所有已知数据点上的函数值 。
-
利用Lagrange插值公式,计算出待插值点 的函数值 。具体公式为 。
-
输出插值点 的函数值 。 一维Lagrange插值算法的核心思想是通过构造一个多项式函数来拟合已知数据点,从而获得未知点的函数值。相对于线性插值算法,它可以拟合更复杂的曲线,但是在数据点数量比较大时,计算复杂度会很高,同时也容易出现Runge现象导致插值精度降低。因此,在实际应用中需要根据具体情况来选择合适的插值方法。
插值算法示意图
MATLAB | 插值算法 | 二维interp2插值法 | 附数据和出图代码 | 直接上手