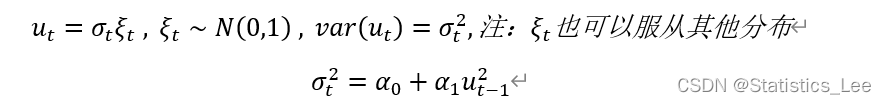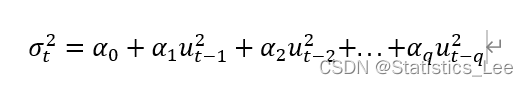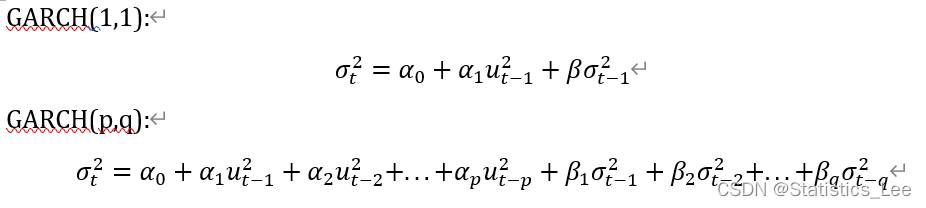ARCH，GARCH模型简介及R语言实现

ARCH和GARCH简介

之前介绍过的ARIMA模型是假定随机扰动的方差是恒定的，这有时候难以适应现实中的金融时间序列模型，如下图所示：

我们发现大的波动往往会聚集在一起，这不符合同方差的假设。

所以我们通过引入条件异方差代替恒定方差的假定，构建了自回归条件异方差模型(ARCH)，为了能应用ARCH或GARCH模型，我们须检验时间序列是否存在条件异方差。

H0：不存在ARCH效应； H1：存在ARCH效应

ARCH(1)模型是最简单的GARCH模型

ARCH(1):

在ARCH1模型下，条件方差是自回归的，即ut的方差由ut滞后一期的平方值决定,在此我们以股票收益率去理解这个模型，假若ut为股票收益率，若昨天风平浪静，没有任何重大的干扰股市的新闻，那么ut-1理应波动不大，既然ut-1不大，那么ut当天的方差波动也不大，今天跟昨天差不多是小波动，若发生重大时间，严重影响股市收益率，则ut-1应较大，那么ut当天的方差波动也会变大，这种大波动跟着大波动，小波动跟着小波动的现象称为波动聚集 

ARCH(q):

 GARCH(p,q)(广义自回归条件异方差模型)，GARCH模型相较与ARCH模型进一步引入了方差的滞后项：

注：GARCH(1,1)模型足以捕捉大多数情况下的波动聚集

这里我们以微软的股价为例，构建ARCH及GARCH模型

基于ARCH和GARCH模型的微软股价收益率的R语言建模

加载包

list.packages