数学建模Matlab之数据预处理方法

04-18 1699阅读

本文综合代码来自文章http://t.csdnimg.cn/P5zOD

异常值与缺失值处理

%% 数据修复
% 判断缺失值和异常值并修复，顺便光滑噪音，渡边笔记
clc,clear;close all;
x = 0:0.06:10;
y = sin(x)+0.2*rand(size(x));
y(22:34) = NaN; % 模拟缺失值
y(89:95) = 50;% 模拟异常值
testdata = [x' y'];
subplot(2,2,1);
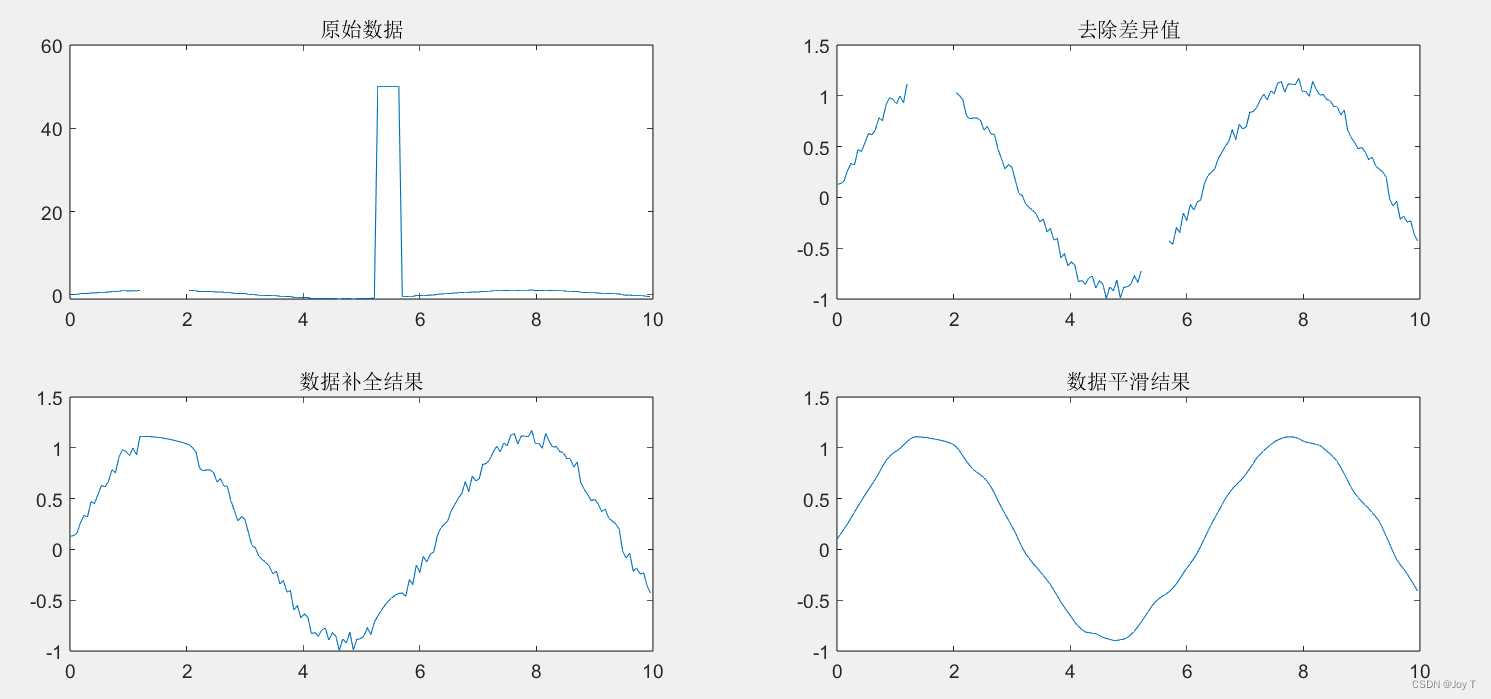
plot(testdata(:,1),testdata(:,2)); %subplot在一个图窗中创建多个子图，然后使用plot函数将原始数据可视化
title('原始数据');

异常值检验

作者通常首先判断是否具有异常值，因为如果有异常值的话，咱们就会剔除异常值，使其变成缺失值，然后再做缺失值处理会好很多。

%% 判断数据中是否存在异常值
% 1.mean 三倍标准差法 2.median 离群值法 3.quartiles 非正态的离群值法
% 4.grubbs 正态的离群值法 5.gesd 多离群值相互掩盖的离群值法
choice_1 = 5;
yichangzhi_fa = char('mean', 'median', 'quartiles', 'grubbs','gesd');
yi_chang = isoutlier(y,strtrim(yichangzhi_fa(choice_1,:))); %选择的是gesd多离群值……
if sum(yi_chang)
    disp('数据存在异常值');
else
    disp('数据不存在异常值');
end

对于上面的异常值检验法做讲解与扩展：

1. Mean 三倍标准差法（3σ原则）

描述：在正态分布数据中，任何一个数值如果偏离平均值超过3倍的标准差，就被认为是异常值。
应用条件：数据基本呈正态分布。（非常重要，需要进行正态性检验）

场景：适用于各种连续数据的分析，例如金融、生物统计等领域。

2. Median 离群值法

描述：基于中位数和四分位数范围来识别异常值。
应用条件：不需要数据完全符合正态分布。

场景：适用于偏态分布或者非正态分布的数据。

3. Quartiles 非正态的离群值法

描述：通过计算数据的四分位数范围（IQR）和上下四分位数来检测异常值。
应用条件：适用于非正态分布的数据。

场景：在各种非正态分布的数据分析中都可以使用。

4. Grubbs 正态的离群值法

描述：基于正态分布假设，测试数据集中最大或最小值是否显著偏离其余的观测值。
应用条件：数据应该是正态分布。

场景：广泛应用于各种领域，尤其是实验数据分析。

5. GESD（Generalized Extreme Studentized Deviate）

描述：用于检测多个异常值，即使它们相互掩盖。
应用条件：不特定于某一分布。

场景：当异常值可能相互掩盖时使用，例如在时间序列分析中。

其他方法

Tukey’s Fences：
- 通过四分位数范围（IQR）和“fences”（上下界）识别异常值。
- 适用于各种分布的数据。
DBSCAN（Density-Based Spatial Clustering of Applications with Noise）:
- 一种基于密度的聚类算法，能够识别簇内和簇外点。
- 用于大数据集和空间数据。

Isolation Forests：

用于高维数据集的异常检测。
通过随机分离点来检测异常值。

正态性检验

读者不难发现，异常值检验通常与数据是否符合正态分布有关，所以，我们一起讨论一下如何使用matlab进行正态性检验。

初步判断

利用图像进行初步的正态性判断，涉及到常见的两种图：Q-Q图和P-P图。

PP图：
- PP图是用于比较两个数据集的累积分布函数（CDF）。
- 当你有一个样本数据集和一个理论分布（如正态分布）时，PP图会比较样本数据的CDF和理论CDF。
- 在正态PP图中，如果样本数据来自正态分布，那么数据点应该大致沿着45度线。
QQ图：
- QQ图是用于比较两个数据集的分位数。QQ图更常用于正态性检验，因为它对尾部的差异更敏感。
- 当你有一个样本数据集和一个理论分布时，QQ图会比较样本数据的分位数和理论分布的分位数。
- 在正态QQ图中，如果样本数据来自正态分布，那么数据点应该大致沿着一条直线，这条线不一定是45度线，但是应该是线性的。

其实上面最重要的一点就是，数据点在两个图中都沿着标准正态分布直线近似分布的话，我们就可以初步判断数据具有正态分布性。

% 正态检验
% 生成一些随机数据
data = randn(100, 1);
% 创建一个新的图形窗口
figure;
% 使用 normplot 创建正态概率图 (QQ图)
subplot(1,2,1);
normplot(data);
title('Normal Q-Q Plot');
% 使用 probplot 创建PP图
subplot(1,2,2);
probplot('normal', data);
title('Normal P-P Plot');

可以在论文中这样写：

为了对数据集的分布特性进行深入理解和分析，本文采用了QQ图和PP图两种方法进行了初步的正态性检验，旨在从不同角度全面评估数据的分布状态。其结果如图1所示。

图1 xx数据PP图(左)和QQ图(右)

图1结果显示：在QQ图中，xx数据的尾部行为和中心趋势没有发现显著的异常值或者偏态现象，表现出良好的正态分布特征；在PP图中，xx数据的整体分布与正态分布非常接近，进一步证实了数据的正态性。综合以上分析结果可初步得知：xx数据集呈现出较强的正态分布特性。

尽管PP图和QQ图都是强大的工具，但它们主要用于探索性数据分析，并不能代替更正式的正态性检验方法，如Jarque-Bera测试或Lilliefors测试。

正式判断

% 正态检验
% 生成一些随机数据
data = randn(100, 1);
% 使用 jbtest 进行 Jarque-Bera 测试
[h_jb, p_jb] = jbtest(data);
% 使用 lillietest 进行 Lilliefors 测试
[h_lil, p_lil] = lillietest(data);
% 显示测试结果
fprintf('Jarque-Bera Test: h = %d, p = %f\n', h_jb, p_jb);
fprintf('Lilliefors Test: h = %d, p = %f\n', h_lil, p_lil);

在上述代码中，h 和 p 分别代表假设检验的结果和 p 值，可以用来判断数据是否符合正态分布。

h = 0 表示在给定的显著性水平下，不拒绝数据来自正态分布的原假设。即，数据可以被认为是正态分布的。

p 值是一个概率值，它表示观察到的数据与正态分布之间的差异是偶然产生的概率。一般来说，如果 p 值大于预定的显著性水平（例如，0.05），则接受原假设，认为数据是正态分布的。

故对上图结果进行数据分析（论文中写的多一点啊，这是简要版）：

Jarque-Bera 测试结果:
- h = 0, p = 0.361618
- 因为h为0，并且p值为0.361618（大于通常的显著性水平0.05），所以我们接受原假设，认为数据是正态分布的。
Lilliefors 测试结果:
- h = 0, p = 0.500000
- 同样，h为0，并且p值为0.5，这也指示数据是正态分布的。

异常值处理与缺失值判断

作者所有异常值处理都是先赋空值，不知道还有没有其他的方法……

%% 对异常值赋空值
F = find(yi_chang == 1);
y(F) = NaN; % 令数据点缺失
testdata = [x' y'];

然后就可以和缺失值一起处理了，但是，为了保证文章的严谨性，咱还是需要判断一下是否存在缺失值。并且，不仅仅只判断，如果题目数据特征尤其多，并且有的特征缺失样本太多了，咱建议还是把这些特征删了，这就涉及到最省力法则：

% 假设testdata是一个n行m列的矩阵，每一列代表一个特征
[n, m] = size(testdata);
threshold = 0.8 * n;  % 设置阈值，80%的总样本量
% 遍历每一个特征
for i = 1:m
    % 计算每一列（特征）中非缺失值的数量
    nonMissingCount = sum(~isnan(testdata(:, i)));
    % 如果非缺失值的数量少于阈值，则删除该列（特征）
    if nonMissingCount  
 
填充缺失值 
 
 %% 对数据进行补全
% 数据补全方法选择
% 1.线性插值 linear 2.分段三次样条插值 spline 3.保形分段三次样条插值 pchip
% 4.移动滑窗插补 movmean
chazhi_fa = char('linear', 'spline', 'pchip', 'movmean');
choice_2 = 3;
if choice_2 ~= 4
    testdata_1 = fillmissing(testdata,strtrim(chazhi_fa(choice_2,:))); % strtrim 是为了去除字符串组的空格
else
    testdata_1 = fillmissing(testdata,'movmean',10); % 窗口长度为 10 的移动均值
end
subplot(2,2,3);
plot(testdata_1(:,1),testdata_1(:,2));
title('数据补全结果'); 
 
作者通常喜欢（让队友）使用K最近邻法填补，而且都是用python搞的，so这里不讲。 
平滑处理 
当然，可以根据实际情况进行数据的平滑处理： 
 
 %% 进行数据平滑处理
% 滤波器选择 1.Savitzky-golay 2.rlowess 3.rloess
choice_3 = 2;
lvboqi = char('Savitzky-golay', 'rlowess', 'pchip', 'rloess');
% 通过求 n 元素移动窗口的中位数，来对数据进行平滑处理
windows = 8;
testdata_2 = smoothdata(testdata_1(:,2),strtrim(lvboqi(choice_3,:)),windows) ; 
 
那么，实际情况到底是什么？ 
平滑数据对于某些机器学习模型的训练和性能是有益的，尤其是对于那些对数据中的噪声敏感的模型。下面是一些可能受益于数据平滑的算法： 
 
  
 
 
  
 
决定是否进行数据平滑应该基于对上述因素的综合考虑，而不仅仅是基于特征的数量。在决定平滑之前，最好通过交叉验证来评估平滑对模型性能的实际影响。属于锦上添花的作用。 
总结 
最终的代码综合一下： 
 
 % 判断缺失值和异常值并修复，顺便光滑噪音，渡边笔记
clc,clear;close all;
x = 0:0.06:10;
y = sin(x)+0.2*rand(size(x));
y(22:34) = NaN; % 模拟缺失值
y(89:95) = 50;% 模拟异常值
testdata = [x' y'];
subplot(2,2,1);
plot(testdata(:,1),testdata(:,2)); %subplot在一个图窗中创建多个子图，然后使用plot函数将原始数据可视化
title('原始数据');
%% 判断数据中是否存在缺失值，并使用最省力法则
% 假设testdata是一个n行m列的矩阵，每一列代表一个特征
[n, m] = size(testdata);
threshold = 0.8 * n;  % 设置阈值，80%的总样本量
% 遍历每一个特征
for i = 1:m
    % 计算每一列（特征）中非缺失值的数量
    nonMissingCount = sum(~isnan(testdata(:, i)));
    % 如果非缺失值的数量少于阈值，则删除该列（特征）
    if nonMissingCount  
 
 
  
 
至此，数据预处理完成。