多叉树题目：子树中标签相同的结点数

文章目录

• 题目
• • 标题和出处
  • 难度
  • 题目描述
  • • 要求
    • 示例
    • 数据范围
    • 解法
    • • 思路和算法
      • 代码
      • 复杂度分析

        题目

        标题和出处

        标题：子树中标签相同的结点数

        出处：1519. 子树中标签相同的结点数

        难度

        5 级

        题目描述

        要求

        给你一个树（即一个连通的无向无环图），这个树由编号从 0 \texttt{0} 0 到 n − 1 \texttt{n} - \texttt{1} n−1 的 n \texttt{n} n 个结点和 n − 1 \texttt{n} - \texttt{1} n−1 条边 edges \texttt{edges} edges 组成。树的根结点为结点 0 \texttt{0} 0，树中的每一个结点都有一个标签，标签是字符串 labels \texttt{labels} labels 中的一个小写字符（编号为 i \texttt{i} i 的结点的标签是 labels[i] \texttt{labels[i]} labels[i]）。

        边数组 edges \texttt{edges} edges 以 edges[i]   =   [a i ,   b i ] \texttt{edges[i] = [a}_\texttt{i}\texttt{, b}_\texttt{i}\texttt{]} edges[i] = [ai​, bi​] 的形式给出，该格式表示结点 a i \texttt{a}_\texttt{i} ai​ 和 b i \texttt{b}_\texttt{i} bi​ 之间存在一条边。

        返回一个大小为 n \texttt{n} n 的数组 ans \texttt{ans} ans，其中 ans[i] \texttt{ans[i]} ans[i] 表示第 i \texttt{i} i 个结点的子树中与结点 i \texttt{i} i 标签相同的结点数。

        树 T \texttt{T} T 的子树是由 T \texttt{T} T 中的某个结点及其所有后代结点组成的树。

        示例

        示例 1：

        

        输入： n   =   7,   edges   =   [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]],   labels   =   "abaedcd" \texttt{n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"} n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"

        输出： [2,1,1,1,1,1,1] \texttt{[2,1,1,1,1,1,1]} [2,1,1,1,1,1,1]

        解释：结点 0 \texttt{0} 0 的标签为 ‘a’ \texttt{`a'} ‘a’ ，以 ‘a’ \texttt{`a'} ‘a’ 为根结点的子树中，结点 2 \texttt{2} 2 的标签也是 ‘a’ \texttt{`a'} ‘a’，因此答案为 2 \texttt{2} 2。注意树中的每个结点都是这个子树的一部分。

        结点 1 \texttt{1} 1 的标签为 ‘b’ \texttt{`b'} ‘b’，结点 1 \texttt{1} 1 的子树包含结点 1 \texttt{1} 1、 4 \texttt{4} 4 和 5 \texttt{5} 5，由于结点 4 \texttt{4} 4、 5 \texttt{5} 5 的标签与结点 1 \texttt{1} 1 不同，因此答案为 1 \texttt{1} 1（该结点本身）。

        示例 2：

        

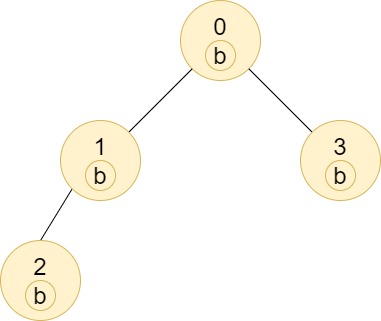
        输入： n   =   4,   edges   =   [[0,1],[1,2],[0,3]],   labels   =   "bbbb" \texttt{n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"} n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"

        输出： [4,2,1,1] \texttt{[4,2,1,1]} [4,2,1,1]

        解释：结点 2 \texttt{2} 2 的子树中只有结点 2 \texttt{2} 2，因此答案为 1 \texttt{1} 1。

        结点 3 \texttt{3} 3 的子树中只有结点 3 \texttt{3} 3，因此答案为 1 \texttt{1} 1。

        结点 1 \texttt{1} 1 的子树中包含结点 1 \texttt{1} 1 和 2 \texttt{2} 2，标签都是 ‘b’ \texttt{`b'} ‘b’，因此答案为 2 \texttt{2} 2。

        结点 0 \texttt{0} 0 的子树中包含结点 0 \texttt{0} 0、 1 \texttt{1} 1、 2 \texttt{2} 2 和 3 \texttt{3} 3，标签都是 ‘b’ \texttt{`b'} ‘b’，因此答案为 4 \texttt{4} 4。

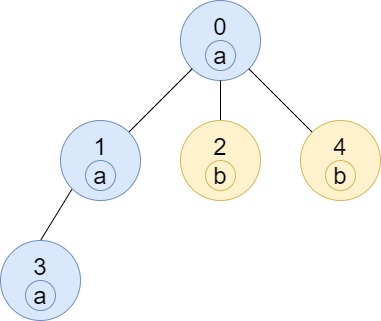
        示例 3：

        

        输入： n   =   5,   edges   =   [[0,1],[0,2],[1,3],[0,4]],   labels   =   "aabab" \texttt{n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"} n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"

        输出： [3,2,1,1,1] \texttt{[3,2,1,1,1]} [3,2,1,1,1]

        数据范围

        • 1 ≤ n ≤ 10 5 \texttt{1} \le \texttt{n} \le \texttt{10}^\texttt{5} 1≤n≤105
        • edges.length = n − 1 \texttt{edges.length} = \texttt{n} - \texttt{1} edges.length=n−1
        • edges[i].length = 2 \texttt{edges[i].length} = \texttt{2} edges[i].length=2
        • 0 ≤ a i ,   b i