C++ 哈希思想应用:位图,布隆过滤器,哈希切分

C++ 哈希思想应用:位图,布隆过滤器,哈希切分

• 一.位图
• • 1.位图的概念
  • • 1.问题
    • 2.分析
    • 3.位图的概念
    • 4.演示
    • 2.位图的操作
    • 3.位图的实现
    • • 1.char类型的数组
      • 2.int类型的数组
      • 3.解决一开始的问题
      • • 位图开多大呢?
        • 小小补充
        • 验证
        • 4.位图的应用
        • • 1.给定100亿个整数，设计算法找到只出现一次的整数？
          • • 1.位图开多大?
            • 2.思路
            • 3.代码
            • 4.验证
            • 2.给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？
            • 3.一个文件有100亿个整数,1G内存,设计算法找到出现次数不超过2次的所有整数
            • 4.给定100亿个整数,0.5G内存,设计算法找到只出现一次的整数？
            • • 1.思路
              • 2.验证代码实现
              • 二.布隆过滤器
              • • 1.布隆过滤器的提出
                • 2.布隆过滤器的概念
                • 3.布隆过滤器的应用场景
                • • 1.能够容忍误判的场景
                  • 2.无法容忍误判的场景
                  • 4.代码实现
                  • • 1.选择字符串哈希函数
                    • 2.推导出布隆过滤器长度
                    • 3.大致结构
                    • 4.具体实现
                    • 5.测试
                    • • 1.小型测试
                      • 2.大型测试
                      • 5.标准非STL容器 : bitset
                      • • 验证
                        • 改造
                        • 6.布隆过滤器的优缺点
                        • 三.哈希切分
                        • • 1.给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法
                          • • 1.近似算法
                            • 2.精确算法
                            • 2.给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？与上题条件相同，如何找到top K的IP？如何直接用Linux系统命令实现？
                            • 四. 如何扩展BloomFilter使得它支持删除元素的操作?
                            • • 1.布隆过滤器删除的局限及其问题
                              • 2.代码
                              • 3.验证布隆过滤器删除的坑点
                              • 4.使用额外的数据结构来进行扩展
                              • • 1.如何做呢?
                                • 2.代码
                                • 3.验证

                                  一.位图

                                  1.位图的概念

                                  1.问题

                                  给你40亿个不重复的无符号整数,没排过序.给一个无符号整数,如何快速判断一个数是否在这40亿个数中?

                                  2.分析

                                  1 Byte = 8 bit

                                  1KB = 1024 Byte

                                  1MB = 1024KB = 10241024 大约= 10的6次方Byte

                                  1GB = 1024MB = 102410的6次方 大约= 10的9次方Byte = 10亿字节

                                  因此4GB 约等于40亿字节

                                  其实最快的方式就是记住1GB约等于10亿字节,这种题就好算了

                                  我们知道40亿个整数,大概就是16GB

                                  如果用排序+二分,

                                  排序需要开16GB大的数组,就算用外排序(归并排序)排完序了,但是二分也需要数组啊…

                                  如果用AVL树红黑树和哈希表

                                  红黑树:三叉链结构+颜色 AVL树:三叉链结构+平衡因子 哈希表:负载因子每个节点的next指针等问题

                                  内存当中更存不下

                                  因此就需要用到位图了

                                  3.位图的概念

                                  

                                  4.演示

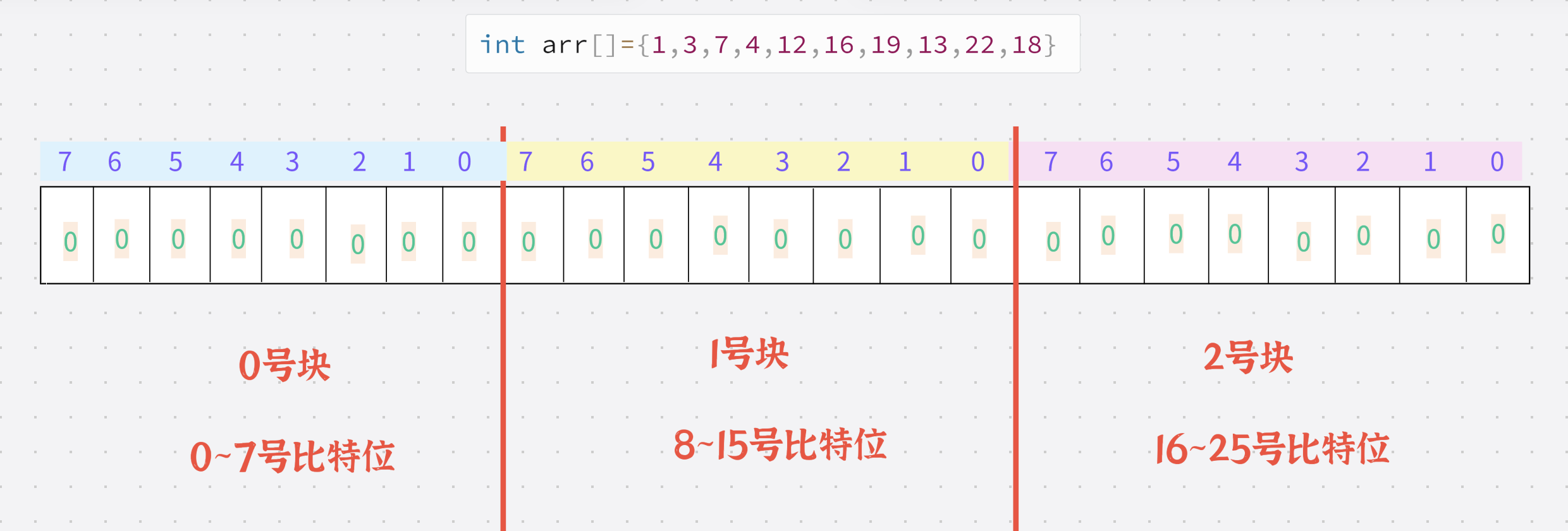
                                  假设我们的位图使用一个char类型的数组实现的话

                                  我们这个arr数组的最大值是22,因此只需要22个比特位即可

                                  因此我们用一个char类型的数组,数组中有3个char即可

                                  存放之前:

                                  

                                  存放方式:

                                  

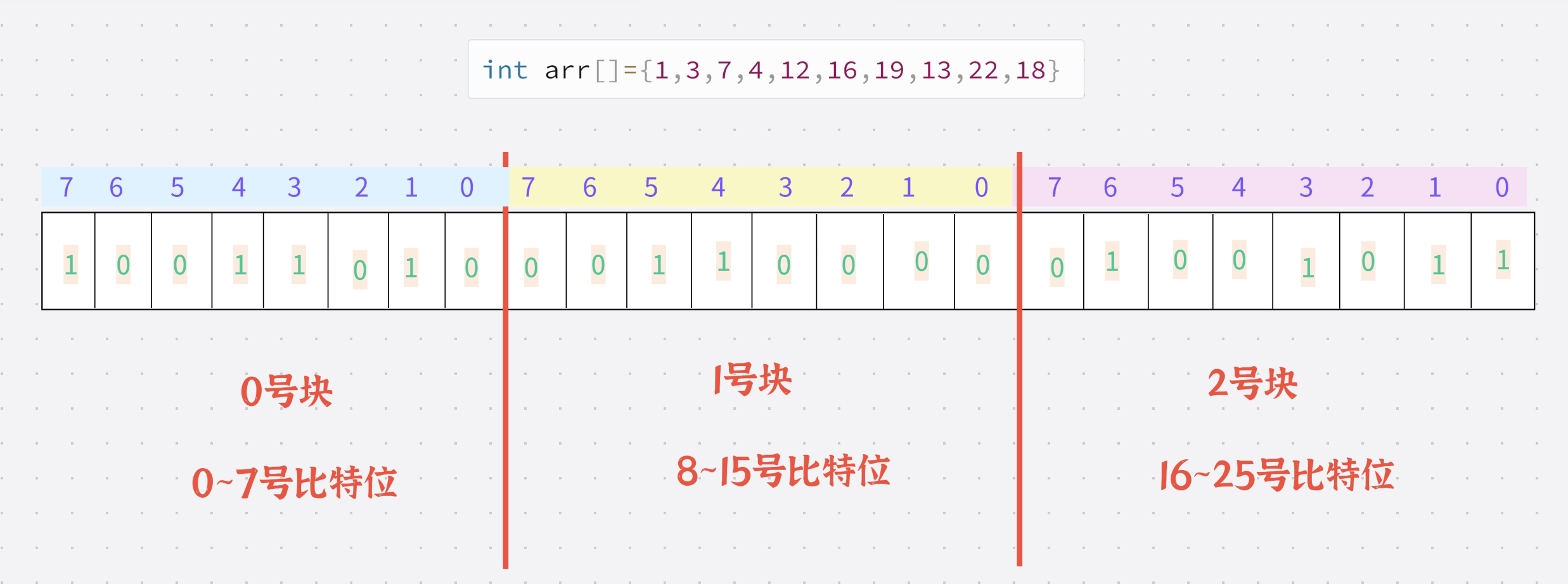
                                  存放过程:

                                  

                                  存放完毕后:

                                  

                                  2.位图的操作

                                  位图的三个核心操作:

                                  set将x对应的比特位设置为1

                                  将某一个比特位置为1,同时不影响其他比特位:

                                  按位或一个数,这个数对应的那个比特位为1,其余比特位为0

                                  void set(size_t x)
                                  {
                                  	size_t i = x / 8;
                                  	size_t j = x % 8;
                                  	_bits[i] |= (1 
                                  	size_t i = x / 8;
                                  	size_t j = x % 8;
                                  	_bits[i] &= ~(1 
                                  	size_t i = x / 8;
                                  	size_t j = x % 8;
                                  	return _bits[i] & (1
                                  	// N是需要多少比特位
                                  	template
                                  	public:
                                  		bitset()
                                  		{
                                  			_bits.resize(N/8+1, 0);
                                  		}
                                  	
                                  		void set(size_t x)
                                  		{
                                  			size_t i = x / 8;
                                  			size_t j = x % 8;
                                  			_bits[i] |= (1 
                                  			size_t i = x / 8;
                                  			size_t j = x % 8;
                                  			_bits[i] &= ~(1 
                                  			size_t i = x / 8;
                                  			size_t j = x % 8;
                                  	
                                  			return _bits[i] & (1
                                  	// N是需要多少比特位
                                  	template
                                  	public:
                                  		bitset()
                                  		{
                                  			//_bits.resize(N/32+1, 0);
                                  			_bits.resize((N5) + 1, 0);
                                  		}
                                  		void set(size_t x)
                                  		{
                                  			size_t i = x / 32;
                                  			size_t j = x % 32;
                                  			_bits[i] |= (1 
                                  			size_t i = x / 32;
                                  			size_t j = x % 32;
                                  			_bits[i] &= ~(1 
                                  			size_t i = x / 32;
                                  			size_t j = x % 32;
                                  			return _bits[i] & (1
                                  public:
                                  	void set(int x)
                                  	{
                                  		//00 - 01
                                  		if (_bits1.test(x) == false && _bits2.test(x) == false)
                                  		{
                                  			_bits2.set(x);
                                  		}
                                  		//01 - 10
                                  		else if (_bits1.test(x) == false && _bits2.test(x) == true)
                                  		{
                                  			_bits1.set(x);
                                  			_bits2.reset(x);
                                  		}
                                  		//10,不记录了
                                  	}
                                  	//返回x出现了多少次
                                  	//返回2表示2次及以上
                                  	int test(int x)
                                  	{
                                  		if (_bits1.test(x) == false && _bits2.test(x) == false)
                                  		{
                                  			return 0;
                                  		}
                                  		else if (_bits1.test(x) == false && _bits2.test(x) == true)
                                  		{
                                  			return 1;
                                  		}
                                  		return 2;
                                  	}
                                  private:
                                  	bitset
                                  	_bits1.reset(x);
                                  	_bits2.reset(x);
                                  }
                                  
                                  	//-1 -3 -4 -5都是转为无符号之后大于2的31次方的整数
                                  	int a[] = { 1,1,2,2,2,2,5,6,1,9,7,-1,-3,-4,-5 };
                                  	set_int::two_bitset
                                  		if ((size_t)e