第十四届蓝桥杯大赛B组 JAVA 蜗牛 (递归剪枝）

题目描述：

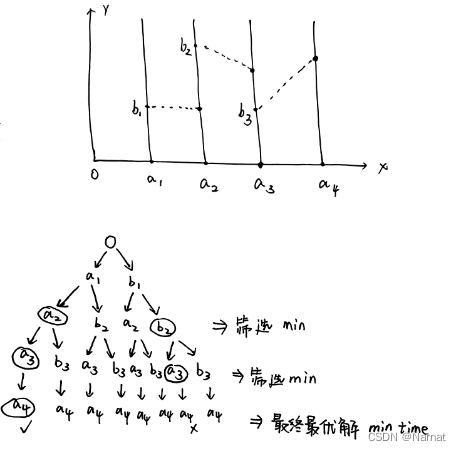
这天，一只蜗牛来到了二维坐标系的原点。 在 x 轴上长有 n 根竹竿。它们平行于 y 轴，底部纵坐标为 0，横坐标分别为 x1, x2,

…, xn。竹竿的高度均为无限高，宽度可忽略。蜗牛想要从原点走到第 n 个竹竿的底部也就是坐标 (xn, 0)。它只能在 x

轴上或者竹竿上爬行，在 x 轴上爬行速度为 1 单位每秒；由于受到引力影响，蜗牛在竹竿上向上和向下爬行的速度分别为 0.7 单位每秒和

1.3 单位每秒。 为了快速到达目的地，它施展了魔法，在第 i 和 i + 1 根竹竿之间建立了传送门（0

bi+1)，请计算蜗牛最少需要多少秒才能到达目的地。 输入格式 输入共 1 + n 行，第一行为一个正整数 n； 第二行为 n 个正整数

x1, x2, . . . , xn； 后面 n − 1 行，每行两个正整数 ai , bi+1。

输出格式：

输出共一行，一个浮点数表示答案（四舍五入保留两位小数）。

样例输入：

3

1 10 11

1 1

2 1

样例输出：

4.20

提示

蜗牛路线：

(0, 0) → (1, 0) → (1, 1) → (10, 1) → (10, 0) → (11, 0)，花费时间为 1+1/0.7+0+1/1.3+1 ≈ 4.20

对于 20% 的数据，保证 n ≤ 15；

对于 100% 的数据，保证 n ≤ 10^5，ai , bi ≤ 10^4，xi ≤ 10^9。

解题思路：

动态规划问题，典型看解析会，自己解就蒙der

分析问题本质，蜗牛由一个杆子到达另一个杆子，要么从本竿的起点出发或本竿的传送点出发，那么问题的核心在于确保到由初始原点到达本竿起点，和到达本竿的传送点必须是最优解

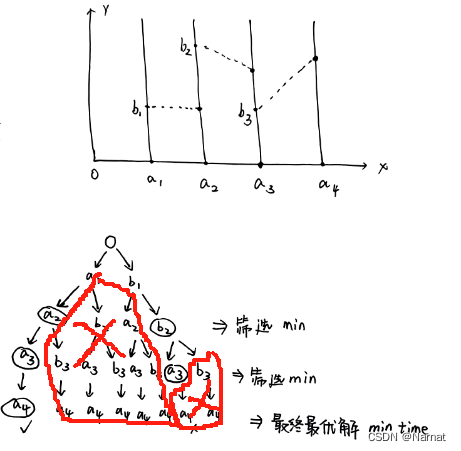
整个示例过程的递归图，以及筛选过程如下：

a2是第二个竹竿的起点o->a1->a2和o->b1->a2的最终效果一样,都是到达第二个竹竿起点，所以保留时间最少的那个即可，同理保留到b2时间最少的那个即可，这便是筛选剪枝

筛选递推公式：

设 x1 表示从起始位置到当前在竹竿底部所需要的最短时间

设 x2 表示从起始位置到当前到达竹竿传送门起点位置的最短时间

则有

x1 = min(两根竹竿的距离差 + x1, x2 + 上一个门终点高度 / 1.3)

x2 = min(两根竹竿的距离差 + x1 + 当前门起点高度 / 0.7, 上一个门终点到当前门所需要的时间 + x2)

最后的目标是遍历到终点的 x1

剪枝后的效果：

代码：

import java.util.Scanner;
public class Main {
    public static void main(String[] args){
         Scanner sc = new Scanner(System.in);
         int n = sc.nextInt();  // 第一行
         int x[] = new int[n + 1];  // x轴
         for(int i = 1; i   // 只有一个竹竿
        	 System.out.printf("%.2f", (double)x[1]);
        	 return;
         }
         
         int door[][] = new int [n][2];  // 存坐标
         for(int i = 1; i