数据结构--堆

文章目录

• 一、堆的概念
• 二、堆的创建
• 三、堆的插入和删除
• 四、堆的应用
• • 1.优先级队列
  • 2.堆排序
  • 3.TopK问题

    一、堆的概念

    对于一个关键码序列的集合来说，K={K0，K1,K2,K3…Kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足Ki=Ki+2),则称为小堆（大堆）。

    堆总是一颗完全二叉树

    

    

    二、堆的创建

    向下调整创建大根堆，以每一个结点为基准，向下调整。

    我们以创建大根堆为例

    

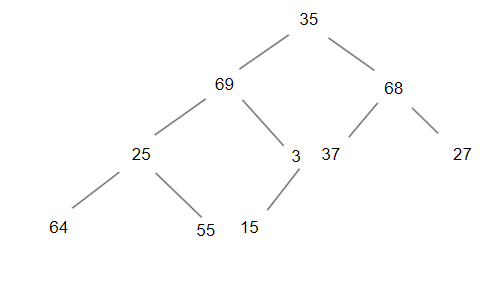
    我们以如上为例进行堆创建的详解

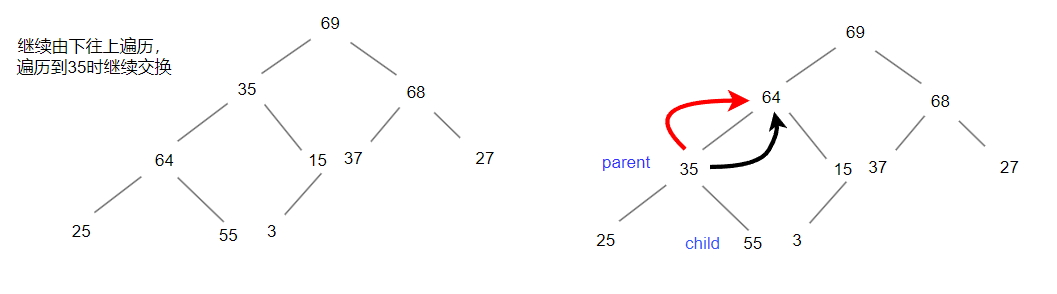
    我们从最下方找到最后一个父亲结点，此时只有一个孩子结点

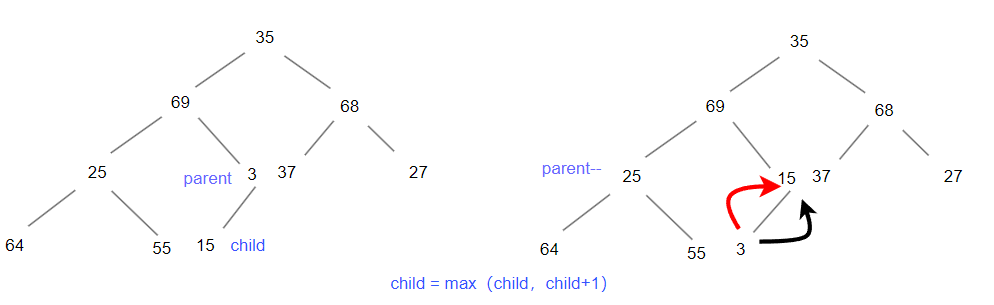
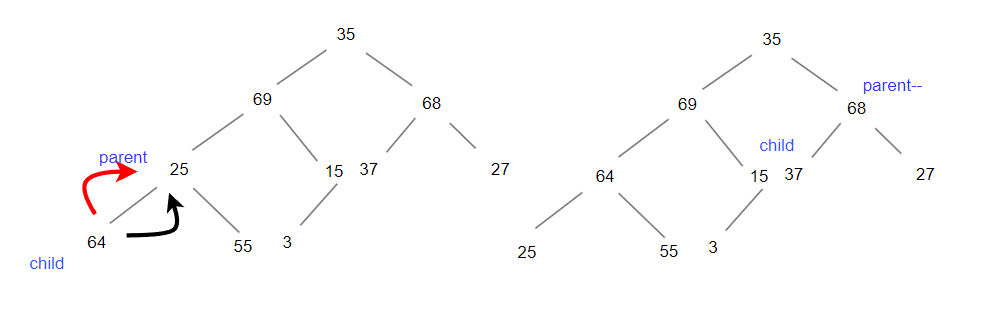
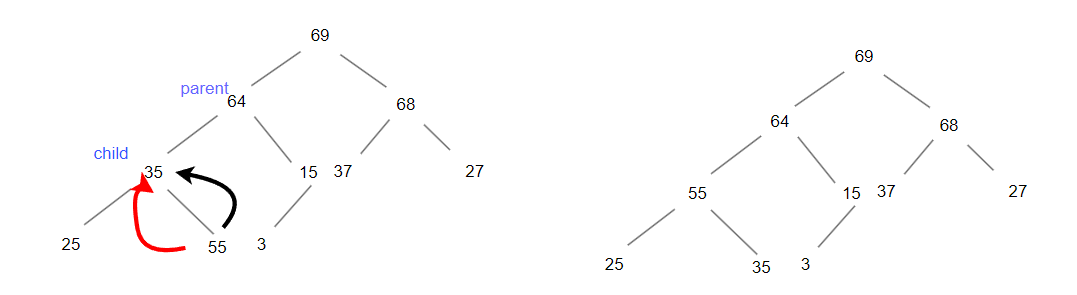
    此时孩子结点的值大于父亲结点，那么交换父亲节点和孩子结点，同时父亲（parent）结点-1，走到下一个要排序的位置，而孩子结点（child= 2*parent+1）我们要取得两个孩子结点中的最大值，与父亲结点进行比较。

    

    

    

    

    

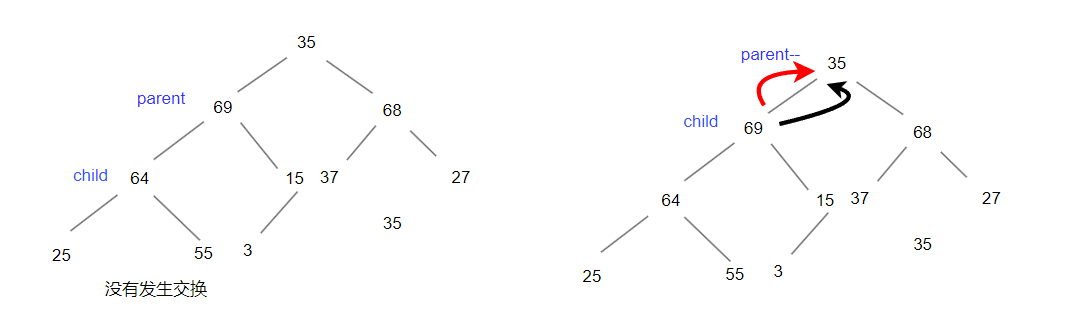
    遍历完成。代码如下

        public TestHeap(){
            this.elem = new int[10];
        }
        public void createBigHeap(){
            for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {
                siftDown(parent,usedSize);
            }
        }
        public void siftDown(int parent,int end){
            int child = parent*2+1;
            while (child  elem[parent]){
                    swap(elem,child,parent);
                    parent = child;
                    child = 2*parent+1;
                }else {
                    break;
                }
            }
        }
        public void swap(int[] elem,int i,int j){
            int temp = elem[i];
            elem[i] = elem[j];
            elem[j] = temp;
        }
    

    建堆的时间复杂度为O（N）。

    三、堆的插入和删除

    堆的插入和删除都是从堆底进行操作，然后再进行向下调整，调整成所需要的堆。

    插入

    

    先将元素42放到底层空间中，之后再对整棵树进行调整。参考堆的创建过程

    删除

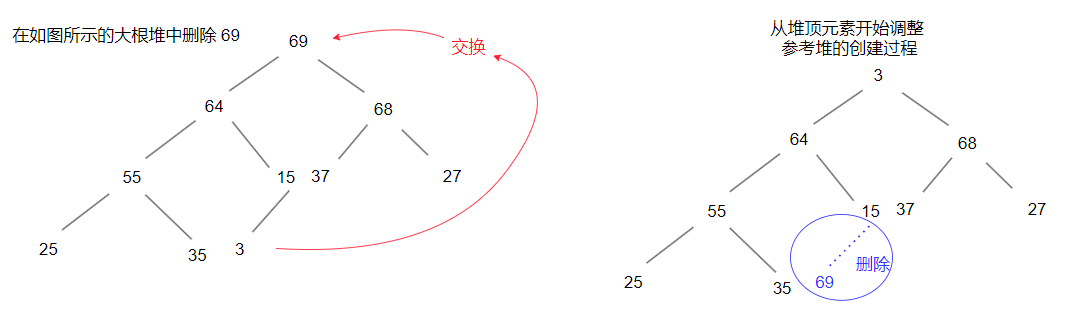
    首先我们要清楚一点，在对堆进行删除操作时，删除的一定是堆顶元素

    

    最终调整成大根堆，

    四、堆的应用

    1.优先级队列

    优先级队列的底层就是由堆实现的，默认的创建的优先级队列是小根堆，

    如果想要建造大根堆的话，需要传入一个比较器，

    class IntCmp implements Comparator{
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2.compareTo(o1);
        }
    }
     public static void main(String[] args) {
            PriorityQueue priorityQueue = new PriorityQueue(new IntCmp());
        }
    

    以下时优先级队列我们一般使用的方法

    函数名	功能介绍
    boolean offer（e)	插入元素e，插入成功会返回true，如果插入对象e为空，则会抛出NullPointerException。时间复杂度为O（log2N）空间不够时，会自动扩容
    E peek（）	获取优先级最高的元素，如果优先级队列为空，则返回null
    E poll（）	获取并移除优先级最高的元素，如果优先级队列为空，则返回null
    int size（）	获取优先级队列中的元素个数
    void clear（）	清空优先级队列
    boolean isEmpty	判断优先级队列是否为空

    2.堆排序

    升序：建立大根堆

    降序：建立小根堆

    我们这里以升序排序为例，为什么不能建立小根堆呢？

    这是因为小根堆我们只能保证根结点是最小的，而不能保证左右结点的大小顺序。

    那么大根堆右如何实现呢？

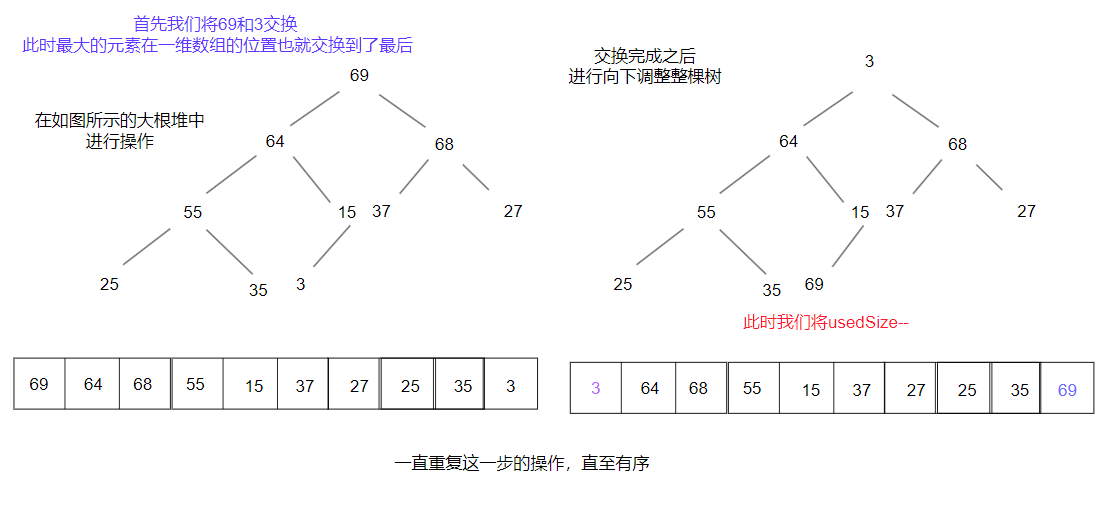
    我们知道堆的元素其实都是存储在一维数组中的，知道了一点，对于理解排序就轻松多了。

    

    同理，降序的原理的也是如此

    3.TopK问题

    力扣链接: 求前k个最小的数

    做题思路如下：

    第一步：

    我们先根据题目要求，来建堆

    前k个最小的元素：建立大根堆

    前k个最大的元素：建立小根堆

    第二步：

    对剩余数组进行遍历依次与堆顶元素进行比较，不符合则直接替换。

    class IntCmp implements Comparator{
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2.compareTo(o1);
        }
    }
     public int[] smallestK(int[] arr, int k) {
            int[] temp2 = new int[k];
            if (k == 0){
                return temp2;
            }
            PriorityQueue priorityQueue = new PriorityQueue(new IntCmp());
            for (int i = 0; i  
    以上就是所有内容，对你有帮助的话，点赞+收藏支持一下吧