FPGA设计篇之双调排序
温馨提示:这篇文章已超过378天没有更新,请注意相关的内容是否还可用!
FPGA设计篇之双调排序(Bitonic Sort)
- 一、写在前面
- 二、双调排序算法原理
- 2.1 双调序列
- 2.2 Batcher定理
- 2.3 双调排序算法
- 2.4 构造双调序列
- 2.5 小结
- 三、双调排序算法RTL实现
- 四、Test_bench
- 五、仿真结果
- 六、写在后面
一、写在前面
在前面,我们介绍了并行全排序算法的原理及RTL级设计,在本文中将继续介绍另外一种排序算法——双调排序算法(Bitonic Sort)的基本原理及其实现。双调排序算法是一种用于排序的并行算法,该算法由Ken Batcher提出。对于含有N个元素的排序网络,该网络中总共需要(N/2)*log2N个排序器,排序时间复杂度为log2N。
二、双调排序算法原理
2.1 双调序列
在讲解双调排序算法前,我们需要了解一个概念——双调序列。双调序列(Botonic Sequence)是指一个由一个非严格增序列X和非严格减序列Y构成的序列,比如序列:2,5,7,12,13,11,6,3或者11,6,3,2,5,7,12,13。这里有一点需要注意的是:双调序列只要求序列是由一个增序列和减序列构成的,并不要求先减后增还是先增后减,也并不要求增序列和减序列等长。
2.2 Batcher定理
Batcher定理:将一个任意长为2N的双调序列a等分为两个等长的序列X和Y,将X中的元素和Y中的元素按照原序进行比较,即将a[i]与a[i+N]进行比较,将较大者放入MAX序列,较小者放入MIN序列,则得到的MAX序列和MIN序列仍然是双调序列,并且MAX序列中的任意一个元素不小于MIN序列中的任意一个元素。
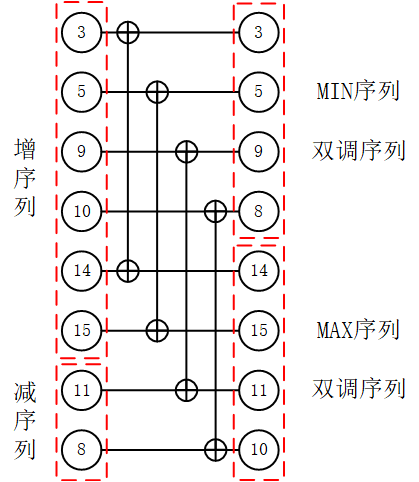
比如序列:3,5,9,10,14,15,11,8,该序列为长度为8的双调序列,其中,序列:3,5,9,10,14,15是增序列,序列:11,8是减序列,将序列等分为两个长度为4的序列,序列一:3,5,9,10;序列二:14,15,11,8,按照顺序将序列一和序列二进行一 一对比,得到MIN序列和MAX序列,其中,MIN序列:3,5,9,8;MAX序列:14,15,11,10。可见,MIN序列与MAX序列均为双调序列,且MAX序列中的任意一个元素均大于MIN序列中的任意一个元素,如下图所示。
2.3 双调排序算法
根据上面提到的Batcher定理,我们可以知道:将一个长度为N的双调序列进行双调排序可以得到两个长度为N/2的双调序列MAX序列和MIN序列,且MAX序列中的值一定不小于MIN序列中的值。那么,由于MAX序列和MIN序列均为双调序列,可以对这两个序列再进行双调排序,MAX序列进行双调排序后得到一个MAXMAX序列和一个MINMAX序列,其中,MAXMAX序列和MINMAX序列的长度均为N/4,且MAXMAX序列中的任意元素的值大于等于MINMAX序列中任意一个元素的值;MIN序列进行双调排序后得到一个MAXMIN序列和一个MINMIN序列,其中MAXMIN序列和MINMIN序列的长度同样为N/4,且MAXMIN序列中的任意一个元素的值大于MINMIN序列中任意一个元素的值。
那么,经过两层的双调排序后,我们得到了4个长度为N/4的双调序列:MAXMAX序列、MINMAX序列、MAXMIN序列、MINMIN序列。这4个序列中任意元素之间的关系如下:
MAXMAX序列 ≥ \geq ≥ MINMAX序列 ≥ \geq ≥ MAXMIN序列 ≥ \geq ≥ MINMIN序列
那么对这4个长度为N/4的双调序列再进行排序,得到依次递增的8个长度为N/8的双调序列(注意:这8个序列之间是依次递增的关系,但是这8个序列内部的数值并不是递增的,而是双调的,即先增后减或者先减后增的序列),按照这个方法一直进行log2N层的双调排序,即可得到排序后的序列。
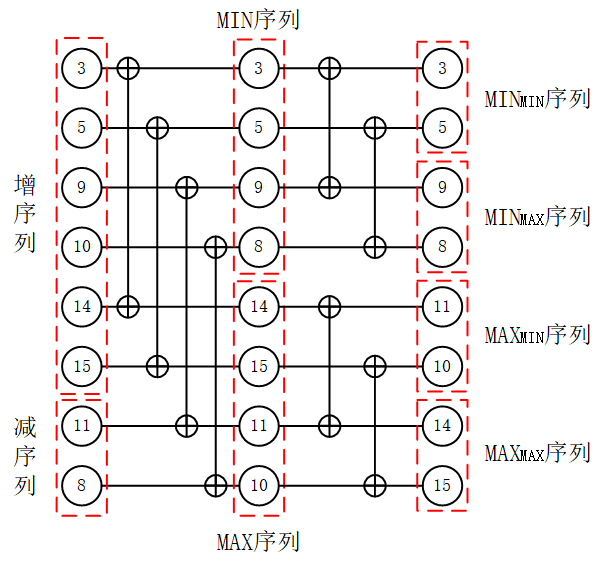
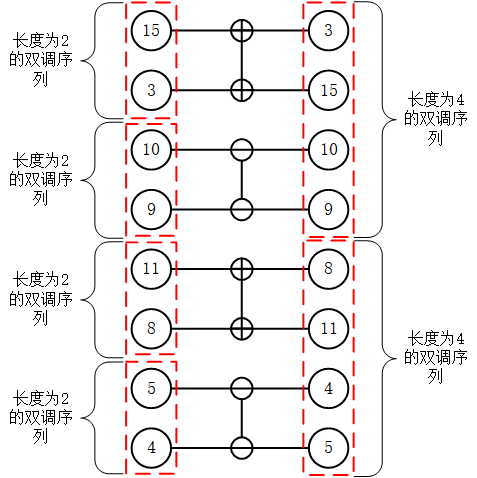
以上面的长度为8的双调序列:3,5,9,10,14,15,11,8为例,对该序列进行双调排序后得到两个长度为4的双调序列MAX序列和MIN序列,其中,MIN序列:3,5,9,8,MAX序列:14,15,11,10,对MIN序列和MAX序列再分别进行双调排序,得到MINMIN序列:3 , 5 ;MINMAX序列:9,8 ;MAXMIN序列:11,10 ; MAXMAX序列:14,15,如下图所示。
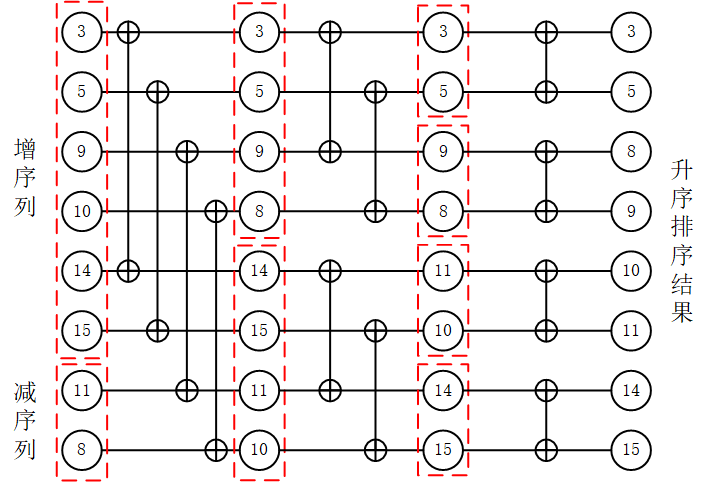
对这4个长度为2的双调序列再分别进行双调排序,即可得到我们需要的排序结果,如下图所示。这里总共进行了log28=3层的双调排序
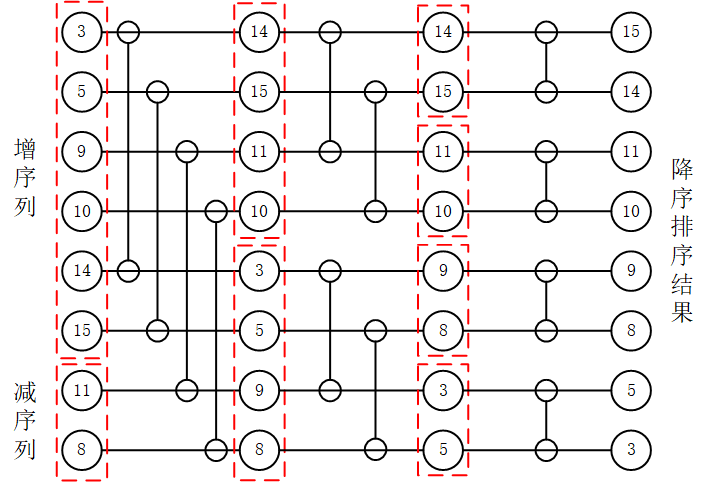
上面用的是升序排序,也可以使用降序排序,得到的排序结果如下图所示。
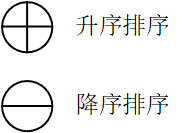
上面,分别示意了升序排序符号和降序排列符号,其符号示意图如下。
2.4 构造双调序列
那么,在我们的日常中,需要进行排序的数据一般都是随机的,并不是双调序列。那么,如果不是双调序列,而是随机生成的序列,双调排序算法是否适用?答案是适用,但是需要先把随机序列转换为双调序列,然后才能使用双调排序算法进行排序,这个过程我们称之为Bitonic Merge。
首先,对于一个长度为2的任意序列,该序列必然是双调序列。而要生成一个长度为4的双调序列,我们只需要让两个长度为2的双调序列单调性相反即可,即一个为增序列,一个为减序列。那么,要如何实现一个为增序列一个为降序列?在前面的双调排序部分,我们知道:对一个长度为N的双调序列进行升序双调排序,即可得到一个长度为N的增序列,而对该序列进行降序双调排序,即可得到一个长度为N的减序列。所以在这里,我们可以分别对这两个长度为2的双调序列进行升序双调排序和降序双调排序,即可得到一个长度为4的双调序列,如下图所示。
那么,对于两个长度为4的双调序列,怎么合成一个长度为8的双调序列?与前面一致,对其中一个双调序列进行升序双调排序,一个进行降序双调排序,即可得到一个长度为8的双调序列,如下图所示。
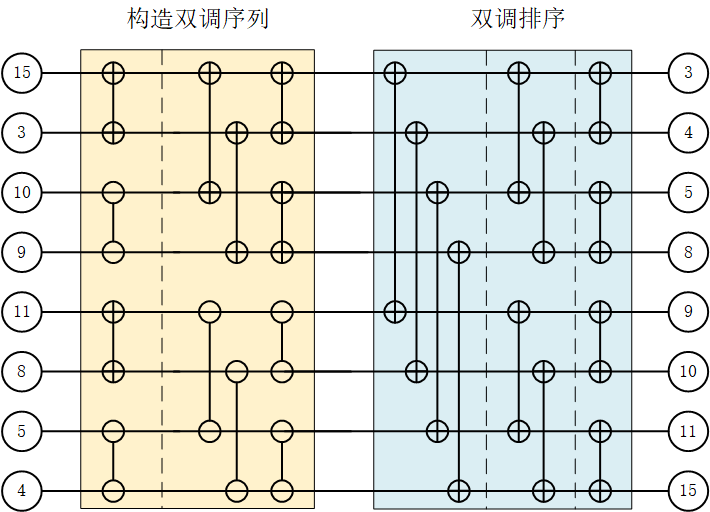
所以,对于一个长度为8的随机序列,经过两次的双调排序,即可得到一个长度为8的双调序列,如下图所示。
综上所述,对于一个长度为N的随机序列,要构造成长度为N的双调序列,可以总结以下几点:
(1)构造一个长度为N的双调序列可以通过两个长度为N/2的单调性相反的序列进行拼接的得到,而长度为N/2的单调序列可以由长度为N/4的双调序列进行双调排序(升序双调排序或者降序双调排序)得到,而长度为N/4的双调序列又可以通过拼接两个长度为N/8的单调性相反的序列得到,而长度为N/8的单调序列又可以由长度为N/4的双调序列进行双调排序(升序双调排序或者降序双调排序)得到…以此类推,直至长度为2的序列,长度为2的序列必然为双调序列。
(2)对于一个长度为N的随机序列,构造成双调序列总共需要 log2N-1 次的双调排序,而所需的比较器个数为: N 2 ∑ 1 l o g 2 N − 1 2 i \frac{N}{2}\sum_{1}^{log_2N-1} 2^i 2N1∑log2N−12i
2.5 小结
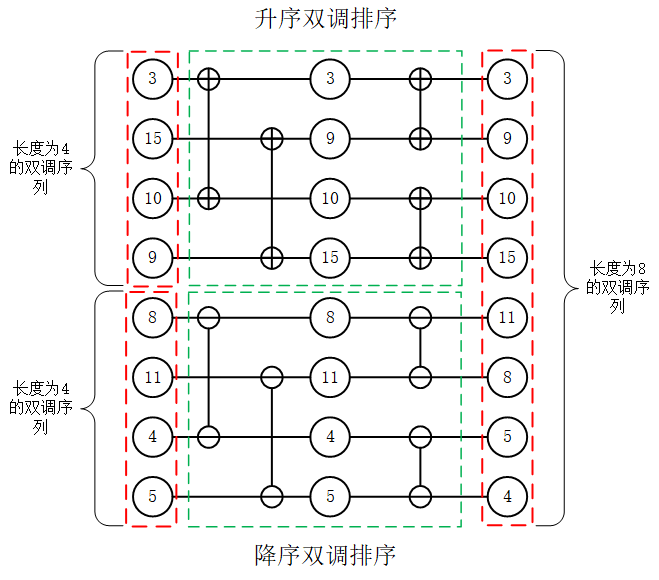
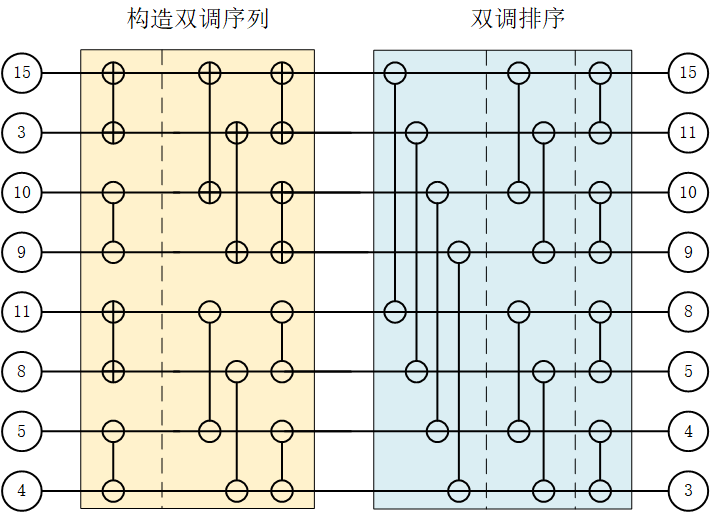
综上所述,对一个随机的序列进行双调排序主要包括两个步骤:(1)构造双调序列;(2)对双调序列进行排序;那么,对于N=8的情况,对其进行升序排序,其排序网络结构如下图所示。
采用降序双调排序,则排序网络结构如下图所示。
三、双调排序算法RTL实现
那么,根据上面讲解的双调排序的基本原理,我们可以编写对应的代码。
首先,我们可以编写编写基本的排序单元——二输入排序单元,可以实现升序排序或者是降序排序,实现对数值以及数值对应的标签进行排序,如下。其中,可以通过参数ASCEND来控制排序器采用升序排序还是降序排序。
module input_2_sequencer #( parameter DATA_WIDTH = 8, parameter LABEL_WIDTH = 4, parameter DATA_NUMBER = 2, parameter ASCEND = 1 ) ( clk, rst_n, data_unsort, label_unsort, data_sorted, label_sorted ); input clk; input rst_n; input [DATA_NUMBER*DATA_WIDTH-1:0] data_unsort; input [DATA_NUMBER*LABEL_WIDTH-1:0] label_unsort; output reg [DATA_NUMBER*DATA_WIDTH-1:0] data_sorted; output reg [DATA_NUMBER*LABEL_WIDTH-1:0] label_sorted; always @(posedge clk or negedge rst_n) if(!rst_n) data_sorted data_unsort[(i+DATA_NUMBER/2)*DATA_WIDTH+:DATA_WIDTH],data_unsort[i*DATA_WIDTH+:DATA_WIDTH]}), .label_unsort({label_unsort[(i+DATA_NUMBER/2)*LABEL_WIDTH+:LABEL_WIDTH],label_unsort[i*LABEL_WIDTH+:LABEL_WIDTH]}), .data_sorted({data_sorted_stage_2[(i+DATA_NUMBER/2)*DATA_WIDTH+:DATA_WIDTH],data_sorted_stage_2[i*DATA_WIDTH+:DATA_WIDTH]}), .label_sorted({label_sorted_stage_2[(i+DATA_NUMBER/2)*LABEL_WIDTH+:LABEL_WIDTH],label_sorted_stage_2[i*LABEL_WIDTH+:LABEL_WIDTH]}) ); end endgenerate // Stage 1 generate for(j=0;jdata_unsort[7],data_unsort[6],data_unsort[5],data_unsort[4],data_unsort[3],data_unsort[2],data_unsort[1],data_unsort[0]}), .label_unsort({label_unsort[7],label_unsort[6],label_unsort[5],label_unsort[4],label_unsort[3],label_unsort[2],label_unsort[1],label_unsort[0]}), .data_sorted({data_sorted[7],data_sorted[6],data_sorted[5],data_sorted[4],data_sorted[3],data_sorted[2],data_sorted[1],data_sorted[0]}), .label_sorted({label_sorted[7],label_sorted[6],label_sorted[5],label_sorted[4],label_sorted[3],label_sorted[2],label_sorted[1],label_sorted[0]}) ); endmodule {{\log }_2}(N) - 2} {{2^i}} *(N/2) i=0∑log2(N)−22i∗(N/2)个二输入的比较器,而进行双调排序使用了 log 2 ( N ) ∗ ( N / 2 ) {\log _2}(N)*(N/2) log2(N)∗(N/2)个二输入的比较器,总共时钟消耗为 ∑ i = 0 log 2 ( N ) − 2 2 i + log 2 ( N ) \sum\limits_{i = 0}^{{{\log }_2}(N) - 2} {{2^i}} + {\log _2}(N) i=0∑log2(N)−22i+log2(N)。