数字信号处理8：利用Python进行数字信号处理基础

我前两天买了本MATLAB信号处理，但是很无语，感觉自己对MATLAB的语法很陌生，看了半天也觉得自己写不出来，所以就对着MATLAB自己去写用Python进行的数字信号处理基础，我写了两天左右，基本上把matlab书上的代码全部用Python实现了，所以，今天贴的代码和图有些多，

要用到的包：

1、Scipy包：其中signal库，这个库是真的绝，很多信号处理的基础函数都有的，

2、numpy包：numpy包中也有很多进行信号处理的，比如说相关、卷积，都有相关函数

3、mmatplotlib包：这就不多说了，信号处理就是用它来展示的，这里主要用到的就是stem方法。

signal库我找了一下，csdn有个博主总结的很全，这是他的博客链接，可以看一看：

(1条消息) scipy.signal信号处理的库（笔记06）_scipy.signalku_月疯的博客-CSDN博客

然后，还可以看一下scipy官方的文档，里面也有很详细的介绍：

Signal processing (scipy.signal) — SciPy v1.10.1 Manual

这里我做了个目录，可以查看相应的方法：

目录

1、离散时间信号序列的表示：

 2、采样定理：

 3、简单离散信号序列：

 4、单位阶跃函数：

5、正弦信号序列：

6、实指数序列：

 7、复指数序列：

8、序列值累加和乘积：

9、序列反转、移位：

 10、信号的尺度变换：

 11、连续信号的奇偶分解：

12、奇函数和偶函数合并：

13、信号的微积分：

 14、积分：

15、卷积运算和相关计算

16、产生信号波形：

 17、连续矩形周期信号采样变成离散信号：

 18、随机函数，这个用numpy就可以直接生成：

 19、三角波，用signal的sawtooth：

 20、sinc曲线:

21、生成非周期三角波

 22、高斯脉冲的实现：

 23、脉冲序列发生器：

24、产生非周期方波：

25、连续时间信号的时域分析

（1）零状态响应：

 （2）冲激响应和阶跃响应：

 （3）各种信号的响应：

（4）连续时间信号的卷积：

26、离散时间系统：

27、离散时间系统的冲激和阶跃响应：

 28、卷积和运算，这都不用说啥了，前面都说过了：

 29、相关序列（自相关、互相关）：

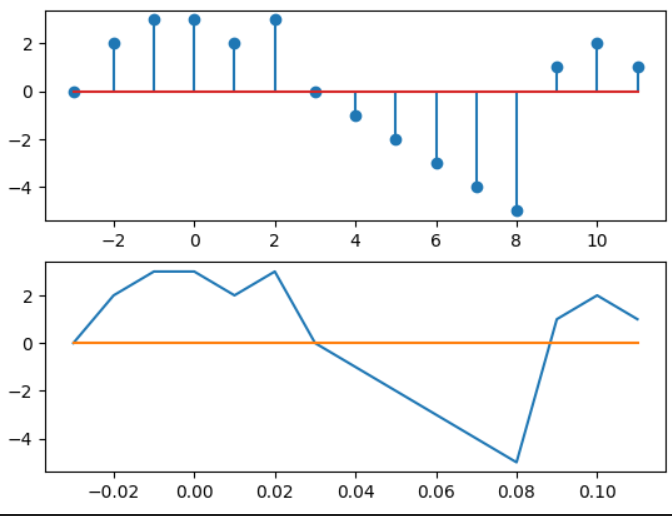
1、离散时间信号序列的表示：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
N=np.linspace(-3,11,15,dtype=int)
x=np.array([0,2,3,3,2,3,0,-1,-2,-3,-4,-5,1,2,1])
dt=0.01
n=N*dt
fig=plt.figure()
ax1=fig.add_subplot(2,1,1)
ax1.stem(N,x)
ax2=fig.add_subplot(2,1,2)
ax2.plot(n,x)
ax2.plot(n,np.zeros(len(n)))

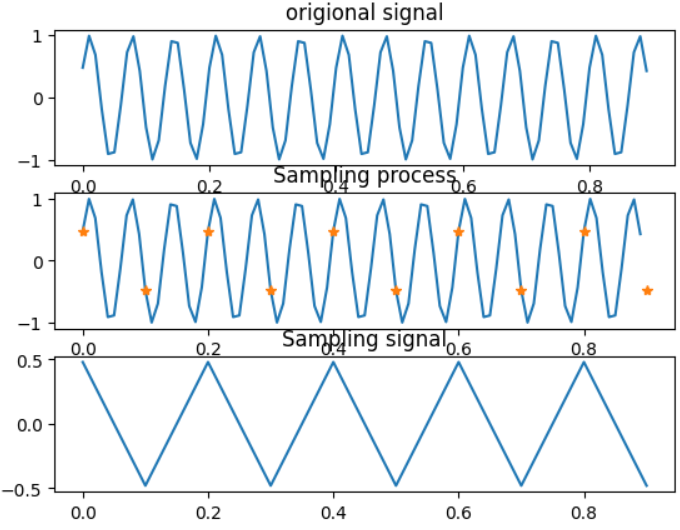
 2、采样定理：

#用10hz的采样频率采样
import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
dt=0.01
n=np.linspace(0,89,90,dtype=int)
t=n*dt
f=10
x=np.sin(3*np.pi*f*t+0.5)#原始信号
dt=0.1
n=np.linspace(0,9,10,dtype=int)
t1=n*dt
x1=np.sin(3*f*np.pi*t1+0.5)# 采样后的信号
fig1=plt.figure()
ax1=fig1.add_subplot(3,1,1)
ax1.plot(t,x)
ax1.set_title('origional signal')
ax2=fig1.add_subplot(3,1,2)
ax2.plot(t,x)
ax2.plot(t1,x1,'*')
ax2.set_title('Sampling process')
ax3=fig1.add_subplot(3,1,3)
ax3.plot(t1,x1)
ax3.set_title('Sampling signal')
plt.show()

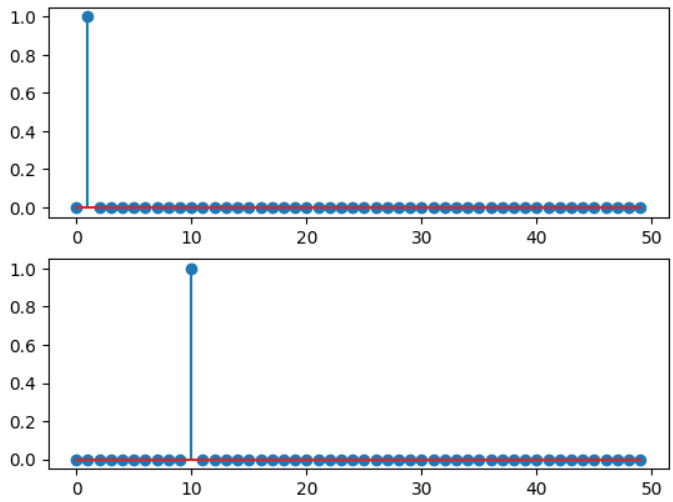
 3、简单离散信号序列：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
n=50
x=np.zeros(n)
x[1]=1
xn=np.linspace(0,n-1,n,dtype=int)
fig1=plt.figure()
ax1=fig1.add_subplot(2,1,1)
ax1.stem(xn,x)
x[1]=0
x[10]=1
ax2=fig1.add_subplot(2,1,2)
ax2.stem(xn,x)
plt.show()

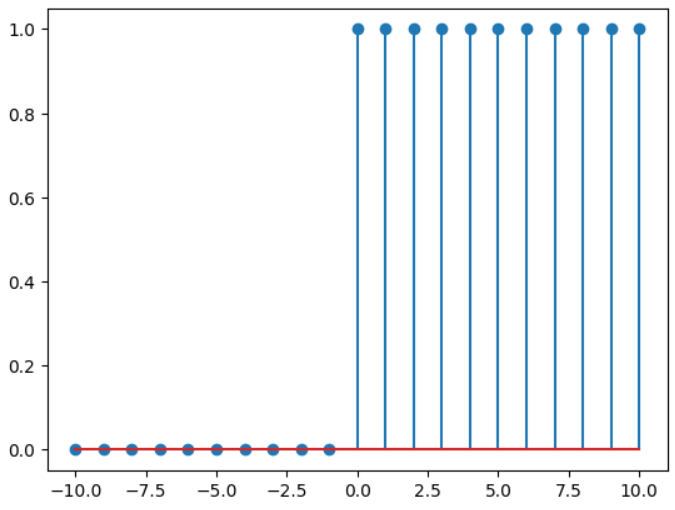
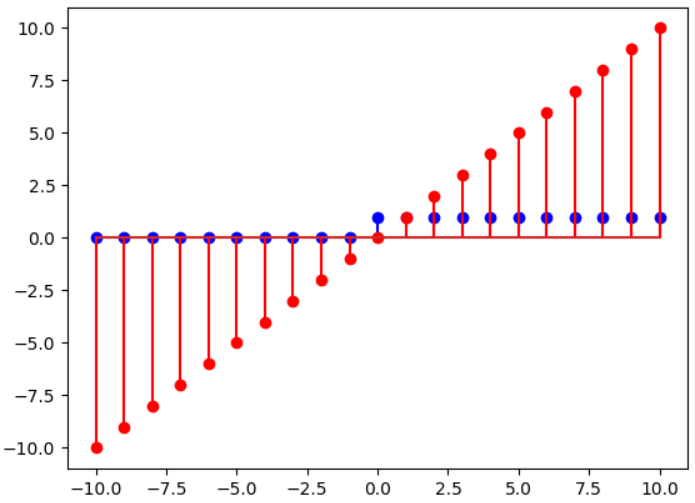
 4、单位阶跃函数：

这个我没有在signal里找到，但是我自己写了一个：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
def u(n):
    if n>=0:
        r=1
    else:
        r=0
    return r
x=np.linspace(-10,10,21,dtype=int)
y=np.array([u(i)for i in x])
plt.stem(x,y)
plt.show()

 很简单的，最简单的是递增序列，就是一个递增函数就行，比如说上面的x，他就是个递增序列：

plt.stem(x,x,'r')

 蓝色的就是刚才的阶跃序列，

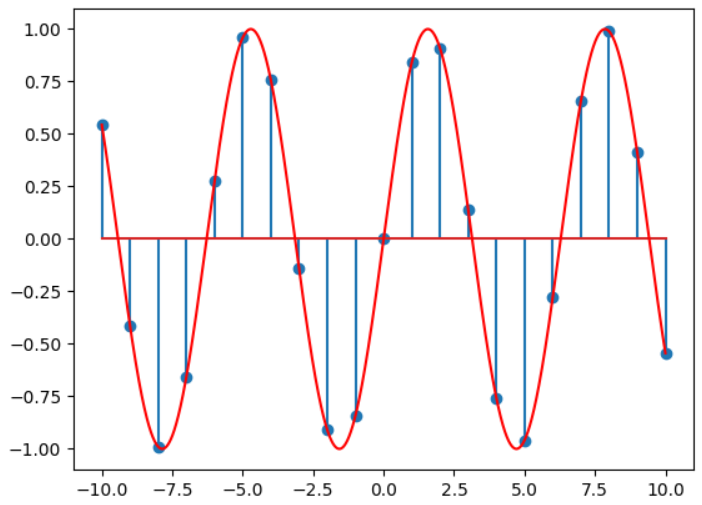
5、正弦信号序列：

这个也很简单，延续上面的代码：

# x=np.linspace(-10,10,21,dtype=int)
# z=np.linspace(-10,10,10000,dtype=float)
plt.stem(x,np.sin(x))
plt.plot(z,np.sin(z),'r')
plt.show()

 可以看到，红色的连续信号和蓝色棉签棒的离散信号。

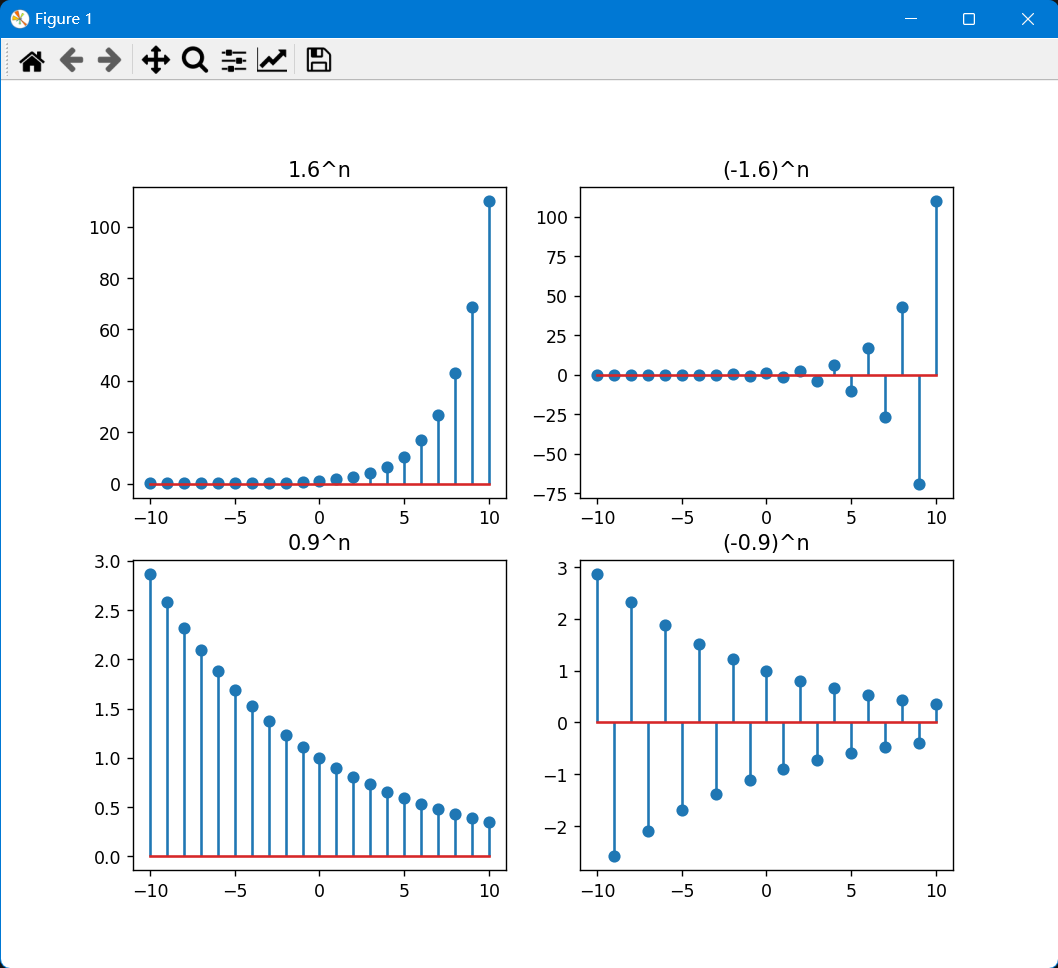
6、实指数序列：

numpy的power函数可以很简单的实现：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
import sympy as sy
n=np.linspace(-10,10,21,dtype=int)
y1=np.power(1.6,n)
y2=np.power(-1.6,n)
y3=np.power(0.9,n)
y4=np.power(-0.9,n)
f=plt.figure()
ax1=f.add_subplot(2,2,1)
ax1.stem(n,y1)
ax2=f.add_subplot(2,2,2)
ax2.stem(n,y2)
ax3=f.add_subplot(2,2,3)
ax3.stem(n,y3)
ax4=f.add_subplot(2,2,4)
ax4.stem(n,y4)
ax1.set_title('1.6^n')
ax2.set_title('(-1.6)^n')
ax3.set_title('0.9^n')
ax4.set_title('(-0.9)^n')
plt.show()

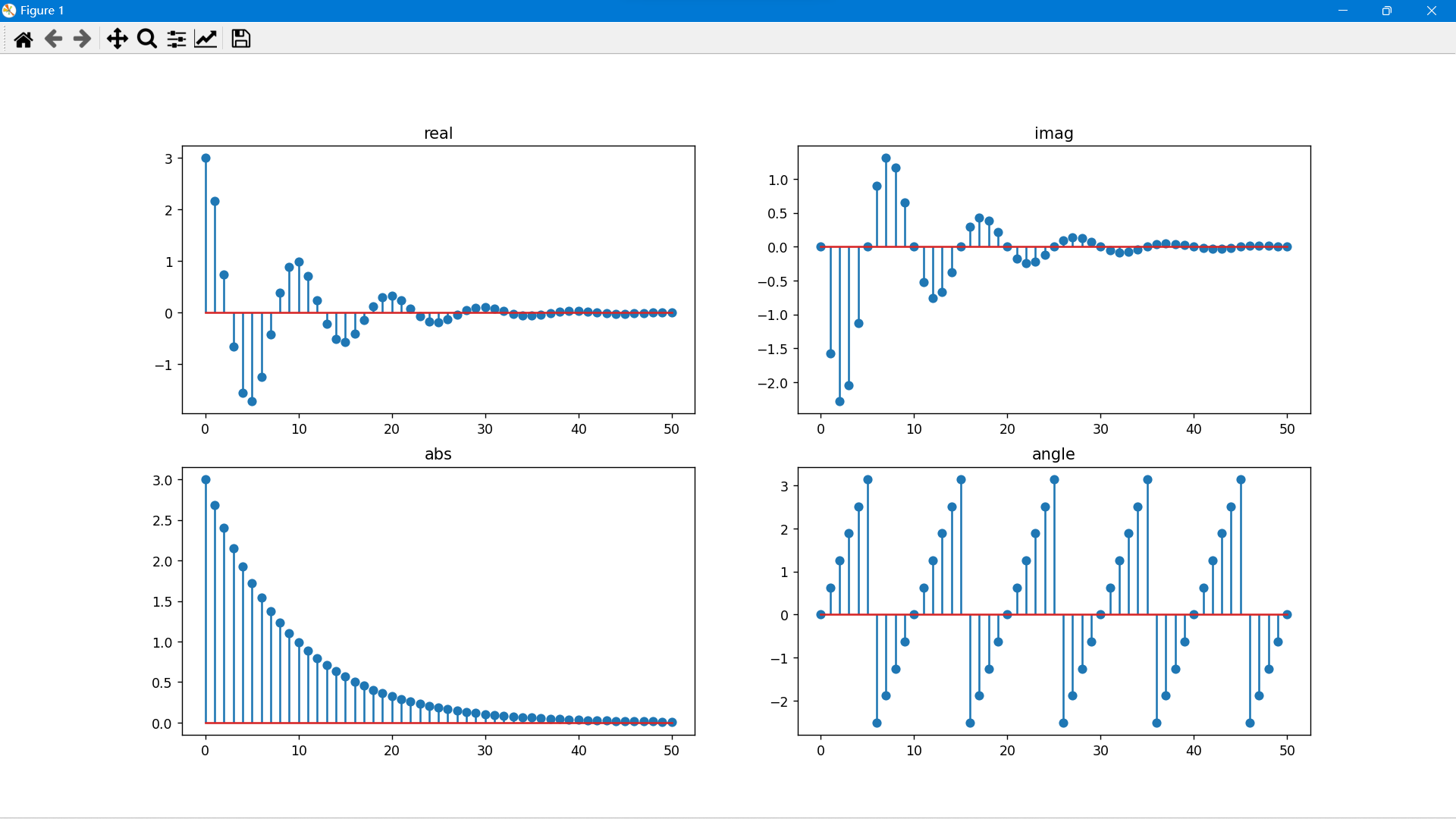
 7、复指数序列：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
import cmath
n=np.linspace(0,50,51,dtype=complex)
A=3
a=-1/9
b=np.pi/5
h=-1/9+np.pi/5j
x=A*np.exp(h*n)
f=plt.figure()
ax1=f.add_subplot(2,2,1)
ax1.stem(n,x.real)
ax2=f.add_subplot(2,2,2)
ax2.stem(n,x.imag)
ax3=f.add_subplot(2,2,3)
ax3.stem(n,abs(x))
ax4=f.add_subplot(2,2,4)
y=np.array([-cmath.phase(i) for i in x])#如果直接用phase的话，和matlab计算的angle是相反的，所以我这里为了和matlab一样，就用了-phase
ax4.stem(n,y)
ax1.set_title('real')
ax2.set_title('imag')
ax3.set_title('abs')
ax4.set_title('angle')
plt.show()

8、序列值累加和乘积：

这个就是常规的numpy操作，没啥意思

9、序列反转、移位：

反转的话，可以用[:：-1]或者也可以用y=np.flipud(x)，两者是一样的效果，信号移位就是，在一个信号序列前面或者后面加一个全零数组，前面加就是延迟，后面加就是提前：

# matlab中有一个函数较fliplr(x)来进行序列反转，但是，python会比这个更简单:两种方法：第一种是用列表反转的形式，第二种是用numpy的flipud函数执行
import numpy as np
import matplotlib.pyplot as plt
nx=np.linspace(-2,5,8,dtype=int)
x=np.linspace(2,9,8,dtype=int)
ny=-np.flipud(nx)
y=np.flipud(x)
print(ny)
print(y)
# ny=-nx[::-1]
# y=x[::-1]
fig=plt.figure()
ax1=fig.add_subplot(2,1,1)
ax1.stem(nx,x,'.')
ax1.axis([-6,6,-1,9])
ax1.grid(visible=True)
ax1.set_xlabel('n')
ax1.set_ylabel('x(n)')
ax1.set_title('origional sequence')
ax2=fig.add_subplot(2,1,2)
ax2.stem(ny,y,'.')
ax2.axis([-6,6,-1,9])
ax2.grid(visible=True)
ax2.set_xlabel('n')
ax2.set_ylabel('y(n)')
ax2.set_title('Inversion sequence')
plt.show()

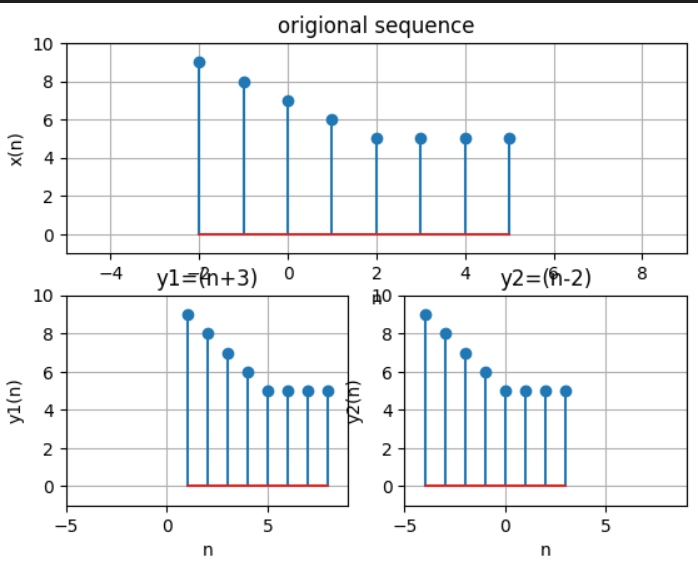
#序列位移：
import matplotlib.pyplot as plt
import numpy as np
nx=np.linspace(-2,5,8,dtype=int)
x=np.array([9,8,7,6,5,5,5,5])
y=x
ny1=nx+3
ny2=nx-2
fig=plt.figure()
ax1=fig.add_subplot(2,1,1)
ax1.stem(nx,x,'.')
ax1.axis([-5,9,-1,10])
ax1.grid(visible=True)
ax1.set_xlabel('n')
ax1.set_ylabel('x(n)')
ax1.set_title('origional sequence')
ax2=fig.add_subplot(2,2,3)
ax2.stem(ny1,y,'.')
ax2.axis([-5,9,-1,10])
ax2.grid(visible=True)
ax2.set_xlabel('n')
ax2.set_ylabel('y1(n)')
ax2.set_title('y1=(n+3)')
ax3=fig.add_subplot(2,2,4)
ax3.stem(ny2,y,'.')
ax3.axis([-5,9,-1,10])
ax3.grid(visible=True)
ax3.set_xlabel('n')
ax3.set_ylabel('y2(n)')
ax3.set_title('y2=(n-2)')
plt.show()

 10、信号的尺度变换：

把信号的横坐标压缩或者扩展：

t = np.linspace(-4, 4, 8000, dtype=float)
T = 2
f = np.zeros((8000),dtype=float)
t1=2*t
f1=np.zeros((8000),dtype=float)
for i in range(len(t)):
    if ((-1