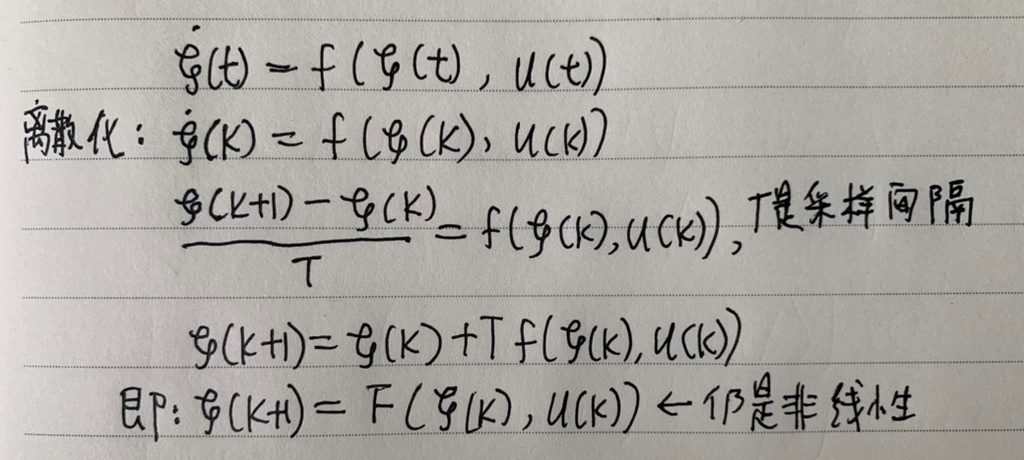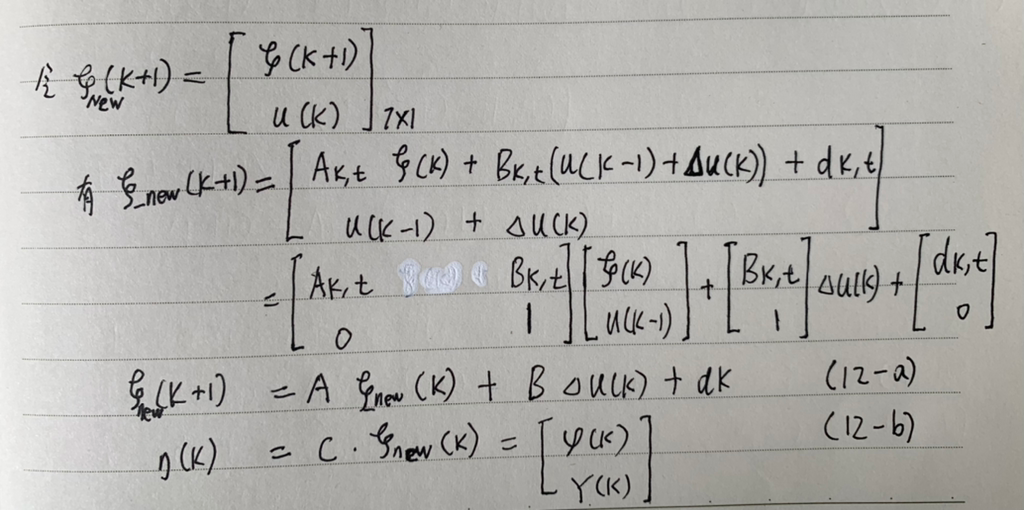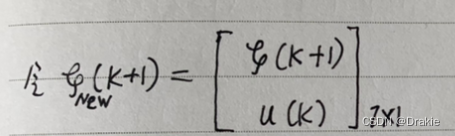基于动力学模型的无人驾驶车辆MPC轨迹跟踪算法及carsim+matlab联合仿真学习笔记
温馨提示:这篇文章已超过384天没有更新,请注意相关的内容是否还可用!
目录
1 模型推导及算法分析
1.1 模型推导
1.1.1 车辆动力学模型
1.1.2 线性时变预测模型推导
1.2 模型预测控制器设计
1.2.1 目标函数设计
1.2.2 约束设计
2 代码解析
2.1 模板框架
2.1.1 S-Function
2.1.2 mdlInitializeSizes函数
2.1.3 mdlUpdates()函数
2.1.4 mdlOutputs()函数
2.2 MPC 算法主体
雅可比矩阵 a b 求解
E 矩阵
参考轨迹 Y ref
H 矩阵
f 矩阵
约束矩阵
quadprog 求解器
3. carsim、simulink联合仿真
3.1 Carsim 设置
3.1.1 车辆参数设置
3.1.2 仿真工况设置
3.1.3 输入输出设置
3.1.4 仿真结果:图形曲线
3.1.5 仿真结果:动画效果
3.2 simulink 仿真
3.2.1 carsim 路径添加
3.2.2 Simulink 搭建
3.2.3 仿真结果
4 不同工况下仿真结果
4.1 控制系统对路面附着条件的鲁棒性
4.2 控制算法对速度的鲁棒性
4.3 不同设计参数对控制器的影响
1 模型推导及算法分析
包括车辆非线性横摆动力学模型、线性时变预测模型推导,以及MPC控制器设计
1.1 模型推导
动力学模型+线性时变预测模型
1.1.1 车辆动力学模型
公式(2.38)是考虑轮胎侧向、纵向滑移的非线性动力学方程,成立的条件是假设前轮偏角 δf 较小,且轮胎模型工作在线性区域。
轨迹跟踪属于横向控制,控制量为小车前轮转角δf。这里默认纵向速度Vx恒定,轨迹跟踪的目的就是使车辆的横摆角 φ 和横向位置 Y 逼近参考轨迹的 φ_ref 和 Y_ref。
选取状态量ξ = [ y_dot, x_dot, φ, φ_dot, Y, X ] ,输出量 η = [ φ ; Y ],于是得到非线性模型:
1.1.2 线性时变预测模型推导
1、离散化:采用前向欧拉法,将非线性公式(2.29)在 k 时刻离散化
2、 线性化
线性化方法泰勒展开首先需要选择一个起始参照点,参照点的选择有参考系统方法,及针对状态轨迹的线性化方法(参照第一版教材3.3.2节,第二版教材这部分内容缺失)。
a. 参考系统方法是指提前得到了每个时刻的参考控制量 Uref,和状态量 ξref 。即在期望轨迹上已经完全通过。这种设计目的是为了消除当前车辆状态和参考系统状态的偏差,本质上不是直接和期望路径进行偏差比对,而是和参考值进行比对。这种方法缺点在于需要提前获取到一个参考系统。本章节的期望轨迹只有 X_predict、Y_ref 及 φ_ref,不包含全部状态,因此无法提前得到一组参考系统,所以采用状态轨迹法。
b. 状态轨迹法:在 t 时刻工作点,对系统施加持续不变的控制量 ut ,得到一条状态轨迹 ξt,并在该 t 时刻做线性化。
难点:这里所谓对系统施加的持续不变的控制量 ut 就是后面用到的恒定量 u(k-1),是在轨迹跟随控制前就已经施加到系统上的控制量,并且这个初始控制量在整个轨迹跟踪过程中都会恒定不变地施加在系统上,不会随着系统状态及控制量的变化而消失,每次求解得到的最优 Δu(k) 只是在上一时刻的 u(k-1) 的基础上补偿的一个增量,这个增量对原本施加在系统上的 ut 即 u(k-1) 没有任何影响,通俗的理解就是 u(k+Np)=u(k-1) + Δu(k) + Δu(k+2) + ... + Δu(k+Np-1) + Δu(k+Np), 即每次求解得到的Δu(k)对控制量的增益改变都会叠加到下一时刻。
难点2:这里的u(k-1)其实就是车辆在没有被施加控制增量时候已经被施加了的控制量,也就意味着是上一时刻的控制量在当前时刻的体现,因为还没有施加控制增量,所以自然可以表示上一时刻的控制量。
先在 t=0 时刻的工作点(ξ0,u0)进行泰勒展开,忽略高阶项:
(11-a)ξ(k + 1)表达式就是线性时变预测模型。 Ak,t 、Bk,t 及 dk,t 表示这是一个时变系统 LTV,需要在线求解系数。这种模型缺点在于表达式中不包含控制量的增量 Δu(k),从而无法使其受到 ΔUmin 和 ΔUmax 的约束,如果在驾驶过程中方向盘的转动幅度过大,会给乘车人带来不好的体验,所以现在需要构造新的形式以便包含对Δu(k)的约束:
1.2 模型预测控制器设计
有了对 Δu(k) 的约束后,就可以开始设计MPC,首先进行目标函数的设计。
1.2.1 目标函数设计
鉴于车辆动力学模型的复杂度较高,加上更多的约束条件,因此控制器在执行过程中,很有可能出现规定时间内求不出最优解的情况,这时车辆方向盘处于失控的危险状态。为了规避这种情况,在目标函数中加入松弛因子ρ。
注意:这里 ρ 越大意味着求解的条件越宽松,但 ρ过大也意味着跟踪效果不理想。
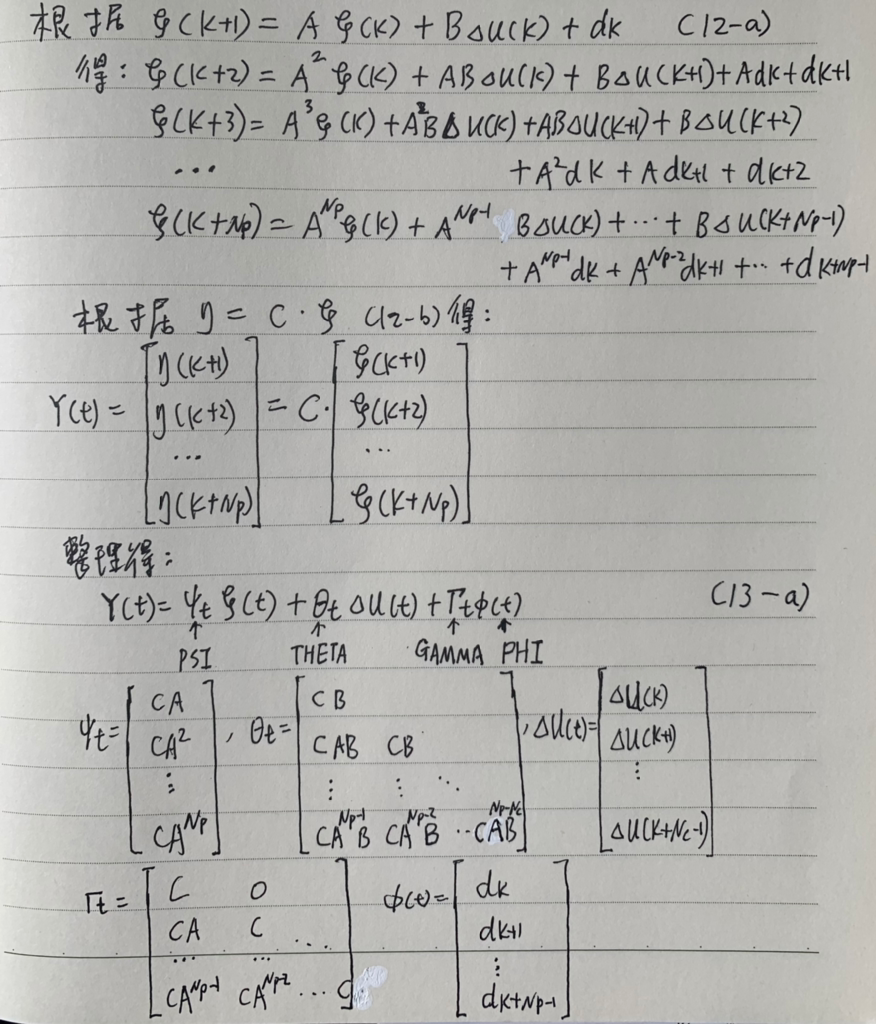
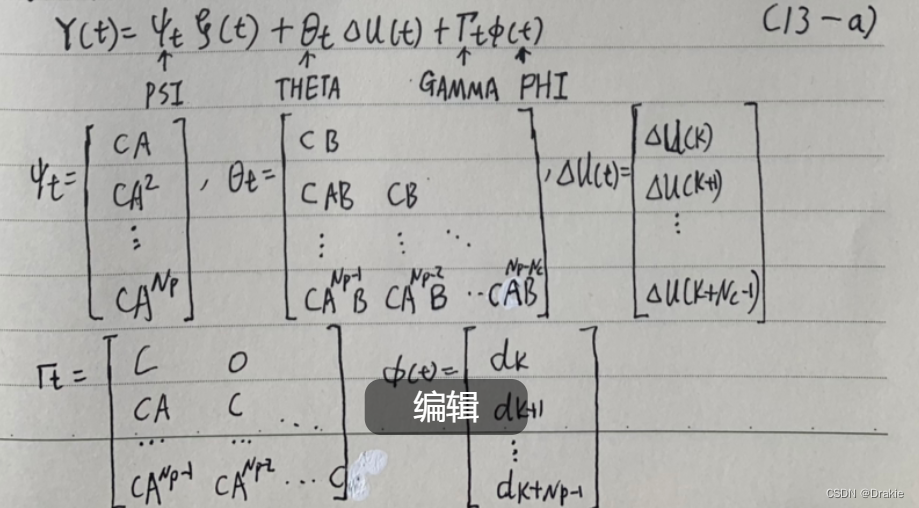
公式(13-a)的 Y(t) 表达式包含了未来 Np 个预测时域内的 ξ(k+i),将 Y(t) 代入目标函数。
公式(13-c)是标准的二次规划形式,其中待求解 X 已经由一维的 Δδf 扩增为包含 ε 的二维增广矩阵,接下来是约束条件的设计。
1.2.2 约束设计
控制量 u(k) 约束及输出量 φ(k) 和 Y(k) 的约束:
控制增量 Δu 的约束:
公式(14-a)是结合了控制量和输出量的综合形式,公式(14-b)是控制增量和松弛因子的约束。到目前为止已经完成轨迹跟踪的线性时变预测模型,接下来的工作是结合代码分析,并结合carsim联合仿真,查看轨迹跟踪效果。
2 代码解析
2.1 模板框架
2.1.1 S-Function
function [sys,x0,str,ts] = chapter5_2_2(t,x,u,flag) % u表示来自carsim的输入
switch flag,
case 0
[sys,x0,str,ts] = mdlInitializeSizes; % 初始化系统参数的一些基本的维度
case 2
sys = mdlUpdates(t,x,u); % 没有用到
case 3
sys = mdlOutputs(t,x,u); % 实现控制算法的主要模块
case {1,4,9}
sys = [];
otherwise
error(['unhandled flag = ',num2str(flag)]);
end
2.1.2 mdlInitializeSizes函数
function [sys,x0,str,ts] = mdlInitializeSizes sizes = simsizes; sizes.NumContStates = 0; % 连续状态量个数为 0 sizes.NumDiscStates = 6; % 离散状态量个数为 6 sizes.NumOutputs = 1; % 输出个数为 1,delta_f 作为输出 sizes.NumInputs = 8; % 输入个数为 8,来自 carsim,还包括2个滑移率 sizes.DirFeedthrough = 1; % mdlOutputs函数模块中直接调用了u的数据,所以为1 sizes.NumSampleTimes = 1; sys = simsizes(sizes); x0 =[0.001;0.0001;0.0001;0.00001;0.00001;0.00001]; % 6个状态量的初始值 global U; % 1维控制量,前轮转角输出 delta_f U=[0]; % delta_f(0)=0,起步时前轮转角为 0° str = []; ts = [0.05 0]; % 仿真间隔是0.05秒,第二项为0表示从0秒开始立即仿真
2.1.3 mdlUpdates()函数
function sys = mdlUpdates(t,x,u) % 这部分没有用到 sys = x;
2.1.4 mdlOutputs()函数
u 表示来自carsim的 8 个状态输入,
function sys = mdlOutputs(t,x,u)
tic % 开始计时
fprintf('Update start, t=%6.3f\n',t) % 日志记录当前时刻控制动作的开始
Nx=6;
Nu=1;
Ny=2;
Np =20;
Nc=5;
T=0.05; % 采样时间
2.2 MPC 算法主体
tic 含义:
下面这部分是车体的参数,目的是为了求解雅可比矩阵 a 和 b
%% a b 常量参数:车体
Sf=0.2; Sr=0.2;
lf=1.232;lr=1.468;
Ccf=66900;Ccr=62700;
Clf=66900;Clr=62700;
m=1723;g=9.8;I=4175;
%% a b 变量参数,carsim 实时采集
y_dot=u(1)/3.6; % Km/h => m/s
x_dot=u(2)/3.6+0.0001; % 防止分母为0
phi=u(3)*3.141592654/180; % degree => rad
phi_dot=u(4)*3.141592654/180;
Y=u(5);
X=u(6);
Y_dot=u(7); % 前轮纵向滑移率
X_dot=u(8); % 后轮纵向滑移率
global U; % 控制量
delta_f=U(1);
fprintf('Update start, u(1)=%4.2f\n',U(1)) % 日志记录每个控制周期的控制量
雅可比矩阵 a b 求解
接下来就是雅可比矩阵 a 和 b 的矩阵表达式,这里只写出了结果:
%% a b
global a b;
a=[ 1 - (259200*T)/(1723*x_dot), -T*(phi_dot + (2*((460218*phi_dot)/5 - 62700*y_dot))/(1723*x_dot^2) - (133800*((154*phi_dot)/125 + y_dot))/(1723*x_dot^2)), 0, -T*(x_dot - 96228/(8615*x_dot)), 0, 0
T*(phi_dot - (133800*delta_f)/(1723*x_dot)), (133800*T*delta_f*((154*phi_dot)/125 + y_dot))/(1723*x_dot^2) + 1, 0, T*(y_dot - (824208*delta_f)/(8615*x_dot)), 0, 0
0, 0, 1, T, 0, 0
(33063689036759*T)/(7172595384320*x_dot), T*(((2321344006605451863*phi_dot)/8589934592000 - (6325188028897689*y_dot)/34359738368)/(4175*x_dot^2) + (5663914248162509*((154*phi_dot)/125 + y_dot))/(143451907686400*x_dot^2)), 0, 1 - (813165919007900927*T)/(7172595384320000*x_dot), 0, 0
T*cos(phi), T*sin(phi), T*(x_dot*cos(phi) - y_dot*sin(phi)), 0, 1, 0
-T*sin(phi), T*cos(phi), -T*(y_dot*cos(phi) + x_dot*sin(phi)), 0, 0, 1];
b=[ 133800*T/1723
T*((267600*delta_f)/1723 - (133800*((154*phi_dot)/125 + y_dot))/(1723*x_dot))
0
5663914248162509*T/143451907686400
0
0];
定义雅可比矩阵 a 和 b 的目的,是为了求解 A 和 B 矩阵:
代码实现:
%% A B C
A_cell=cell(2,2);
A_cell{1,1}=a;
A_cell{1,2}=b;
A_cell{2,1}=zeros(Nu,Nx);
A_cell{2,2}=eye(Nu);
A=cell2mat(A_cell);
B_cell=cell(2,1);
B_cell{1,1}=b;
B_cell{2,1}=eye(Nu);
B=cell2mat(B_cell);
C=[0 0 1 0 0 0 0;
0 0 0 0 1 0 0;];
这里 得到的A 和 B 矩阵的目的是为了得到 ψ θ Γ Φ 矩阵,参考公式(13-a):
由于 θ 同时被矩阵E H f 调用,所以这里可以首先实现 θ:
%% THETA (被 E H f 调用)
THETA_cell=cell(Np,Nc);
for j=1:1:Np
for k=1:1:Nc
if kT_all
X_DOT=x_dot*cos(phi)-y_dot*sin(phi);
X_predict(Np,1)=X+X_DOT*Np*T;
z1=shape/dx1*(X_predict(Np,1)-Xs1)-shape/2;
z2=shape/dx2*(X_predict(Np,1)-Xs2)-shape/2;
Y_ref(p,1)=dy1/2*(1+tanh(z1))-dy2/2*(1+tanh(z2));
phi_ref(p,1)=atan(dy1*(1/cosh(z1))^2*(1.2/dx1)-dy2*(1/cosh(z2))^2*(1.2/dx2));
Yita_ref_cell{p,1}=[phi_ref(p,1);Y_ref(p,1)];
else % 在仿真时长内(正常执行部分)
X_DOT=x_dot*cos(phi)-y_dot*sin(phi); % X的斜率,由非线性动力学公式(2.29给出)
X_predict(p,1)=X+X_DOT*p*T; % X是由carsim输出的车辆当前纵向坐标,X_predict(p,1)表示下一时刻的纵坐标
z1=shape/dx1*(X_predict(p,1)-Xs1)-shape/2;
z2=shape/dx2*(X_predict(p,1)-Xs2)-shape/2;
Y_ref(p,1)=dy1/2*(1+tanh(z1))-dy2/2*(1+tanh(z2)); % 下一时刻的横坐标参考值
phi_ref(p,1)=atan(dy1*(1/cosh(z1))^2*(1.2/dx1)-dy2*(1/cosh(z2))^2*(1.2/dx2)); % 下一时刻的横摆角参考值
Yita_ref_cell{p,1}=[phi_ref(p,1);Y_ref(p,1)]; % [phi_rel; Y_ref]
end
end
Yita_ref=cell2mat(Yita_ref_cell); % Y_ref 矩阵规范化
接下来实现 ψ
%% ψ PSI
PSI_cell=cell(Np,1);
for j=1:1:Np
PSI_cell{j,1}=C*A^j;
end
PSI=cell2mat(PSI_cell);
然后是 ξ,这里 ξ 是经过重构的增广矩阵:
%% ξ kesi
kesi=zeros(Nx+Nu,1); % ξnew(k)=[ξ(k); u(k-1)]
kesi(1)=y_dot;
kesi(2)=x_dot;
kesi(3)=phi;
kesi(4)=phi_dot;
kesi(5)=Y;
kesi(6)=X;
kesi(7)=U(1); % u(k-1)
GAMMA
%% Γ GAMMA
GAMMA_cell=cell(Np,Np); % 维度 20*20
for p=1:1:Np;
for q=1:1:Np;
if q