华为OD机试 - 抢7游戏(Java & JS & Python & C & C++)
温馨提示:这篇文章已超过384天没有更新,请注意相关的内容是否还可用!
题目描述
A、B两个人玩抢7游戏,游戏规则为:
A先报一个起始数字 X(10 ≤ 起始数字 ≤ 10000),B报下一个数字 Y (X - Y
在B赢得比赛的情况下,一共有多少种组合?
输入描述
起始数字 M
- 10 ≤ M ≤ 10000
如:
100
输出描述
B能赢得比赛的组合次数
用例
输入 10 输出 1 说明 无 数学分析解法(可能会超时)
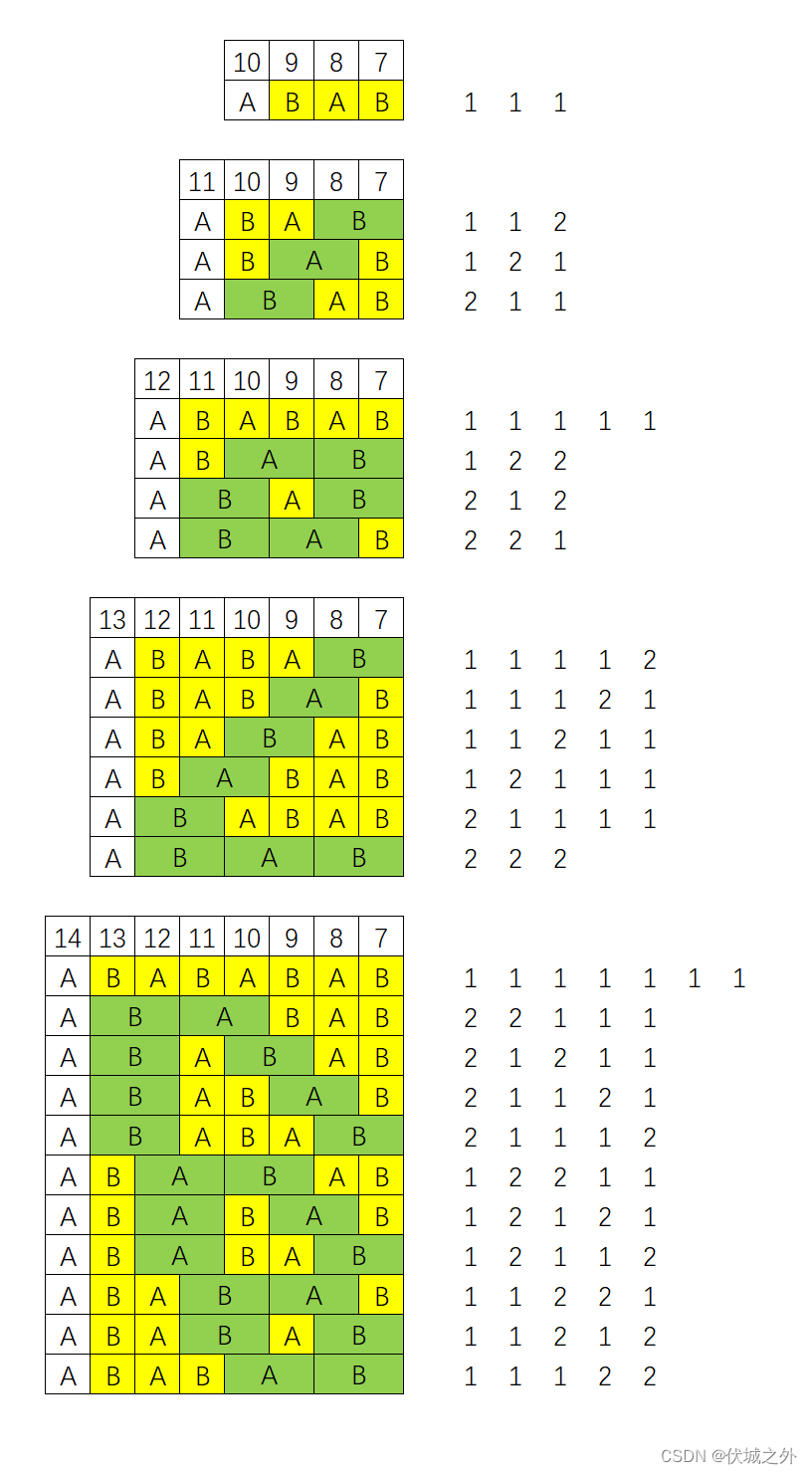
下面模拟M为10~14时,B能够获胜的一些情况:
看完上图,我们可以发现:
抛开A首次叫的数字M,剩下的 M - 7 长度(上图中有颜色的),必须发生奇数次叫,才能保证B获胜。
原因是:奇数次叫中,第一次必然是B,由于是奇数次,因此最后一次也必然是B,比如
BAB
BABAB
都是奇数次。
因此我们只需要将整数 M - 7 划分为奇数块即可,且每块取值只能是1或2。
我们可以假设初始时,一共发生了M-7次叫(M-7可能不是奇数),即每块长度都是1,此时我们设
- oneCount = M - 7
- twoCount = 0
然后检查 oneCount + twoCount 的和(一共叫几次):
- 若为奇数,则计算 oneCount 个 1 和 twoCount 个 2 形成的不重复的全排列的个数,统计进结果ans
- 若为偶数,则B无法获胜
之后,我们应该合并两个1为一个2,即:
- oneCount -= 2
- twoCount += 1
此时就会产生一种新的叫声情况,将新的oneCount和twoCount带入前面逻辑,进行循环处理,知道oneCount
本题的数量级很大,10 ≤ M ≤ 10000,因此满足要求的情况数量可能极端大,此时我们应该使用大数记录结果。
JS算法源码
const rl = require("readline").createInterface({ input: process.stdin }); var iter = rl[Symbol.asyncIterator](); const readline = async () => (await iter.next()).value; void (async function () { const m = parseInt(await readline()); const factor = initFactor(m - 7); let oneCount = m - 7; let twoCount = 0; // 记录B赢的情况数 let ans = BigInt(0); while (oneCount >= 0) { // 叫的次数为奇数时,才能B赢 if ((oneCount + twoCount) % 2 != 0) { ans += getPermutationCount(oneCount, twoCount); } // 合并两个1为一个2 oneCount -= 2; twoCount += 1; } console.log(ans.toString()); // 求解不重复的全排列数 function getPermutationCount(oneCount, twoCount) { // 即 1 1 1 1 1 或 2 2 2 这种情况,此时只有一种排列 if (oneCount == 0 || twoCount == 0) { return BigInt(1); } else { // 排列数去重,比如 1 1 1 2 2 的不重复排列数为 5! / 3! / 2! = 10 return factor[oneCount + twoCount] / factor[oneCount] / factor[twoCount]; } } // 阶乘 function initFactor(n) { const factor = new Array(n + 1); factor[0] = BigInt(1); for (let i = 1; i = 0) { // 叫的次数为奇数时,才能B赢 if ((oneCount + twoCount) % 2 != 0) { ans = ans.add(getPermutationCount(oneCount, twoCount)); } // 合并两个1为一个2 oneCount -= 2; twoCount += 1; } System.out.println(ans); } // 求解不重复的全排列数 public static BigInteger getPermutationCount(int oneCount, int twoCount) { if (oneCount == 0 || twoCount == 0) { // 即 1 1 1 1 1 或 2 2 2 这种情况,此时只有一种排列 return new BigInteger("1"); } else { // 排列数去重,比如 1 1 1 2 2 的不重复排列数为 5! / 3! / 2! = 10 return factor[oneCount + twoCount].divide(factor[oneCount].multiply(factor[twoCount])); } } // 阶乘 public static void initFactor(int n) { factor = new BigInteger[n + 1]; factor[0] = new BigInteger("1"); for (int i = 1; i = 0: # 叫的次数为奇数时,才能B赢 if (oneCount + twoCount) % 2 != 0: ans += getPermutationCount(oneCount, twoCount) # 合并两个1为一个2 oneCount -= 2 twoCount += 1 return ans print("{:.0f}".format(getResult()))C算法源码
下面代码没有实现大数运算,关于大数运算可以参考:
大数运算(加、减、乘、除)-CSDN博客
#include #include // 阶乘 double getFactor(int n) { double ans = 1; for (int i = 2; i = 0) { // 叫的次数为奇数时,才能B赢 if ((oneCount + twoCount) % 2 != 0) { ans += getPermutationCount(oneCount, twoCount); } // 合并两个1为一个2 oneCount -= 2; twoCount += 1; } char res[1000] = {'\0'}; sprintf(res, "%lf", ans); strchr(res, '.')[0] = '\0'; printf("%s", res); return 0; }C++算法源码
#include using namespace std; vector factor; // 阶乘 void initFactor(int n) { factor = vector(n + 1); factor[0] = 1; for (int i = 1; i > m; initFactor(m - 7); int oneCount = m - 7; int twoCount = 0; // 记录B赢的情况数 double ans = 0; while (oneCount >= 0) { // 叫的次数为奇数时,才能B赢 if ((oneCount + twoCount) % 2 != 0) { ans += getPermutationCount(oneCount, twoCount); } // 合并两个1为一个2 oneCount -= 2; twoCount += 1; } cout BigInt(0)); for (let i = m - 1; i >= 7; i--) { // B叫数字i的方案数 = A叫数字i+1的方案数 + A叫数字i+2的方案数 dpB[i] = dpA[i + 1] + dpA[i + 2]; // A叫数字i的方案数 = B叫数字i+1的方案数 + B叫数字i+2的方案数 dpA[i] = dpB[i + 1] + dpB[i + 2]; } console.log(dpB[7].toString()); })();Python算法源码
# 输入获取 m = int(input()) # 算法入口 def getResult(): # dpA[i] 表示 A 叫 数字i 的方案数 dpA = [0 for _ in range(m + 2)] # 由于是A从m开始叫,因此A叫m的方案数为1 dpA[m] = 1 # dpB[i] 表示 B叫 数字i 的方案数 dpB = [0 for _ in range(m + 2)] for i in range(m - 1, 6, -1): # B叫数字i的方案数 = A叫数字i+1的方案数 + A叫数字i+2的方案数 dpB[i] = dpA[i + 1] + dpA[i + 2] # A叫数字i的方案数 = B叫数字i+1的方案数 + B叫数字i+2的方案数 dpA[i] = dpB[i + 1] + dpB[i + 2] # 返回B叫7的方案数 return dpB[7] # 算法调用 print(getResult())C算法源码
下面代码没有实现大数运算,关于大数运算可以参考:
大数运算(加、减、乘、除)-CSDN博客
#include #include #include int main() { int m; scanf("%d", &m); // dpA[i] 表示 A 叫 数字i 的方案数 double dpA[m + 2]; // 初始化dpA[i] for (int i = 0; i = 7; i--) { // B叫数字i的方案数 = A叫数字i+1的方案数 + A叫数字i+2的方案数 dpB[i] = dpA[i + 1] + dpA[i + 2]; // A叫数字i的方案数 = B叫数字i+1的方案数 + B叫数字i+2的方案数 dpA[i] = dpB[i + 1] + dpB[i + 2]; } char res[1000] = {'\0'}; sprintf(res, "%lf", dpB[7]); strchr(res, '.')[0] = '\0'; printf("%s", res); return 0; }C++算法源码
#include using namespace std; int main() { int m; cin >> m; // dpA[i] 表示 A 叫 数字i 的方案数 vector dpA(m + 2, 0); // 由于是A从m开始叫,因此A叫m的方案数为1 dpA[m] = 1; // dpB[i] 表示 B叫 数字i 的方案数 vector dpB(m + 2, 0); for (int i = m - 1; i >= 7; i--) { // B叫数字i的方案数 = A叫数字i+1的方案数 + A叫数字i+2的方案数 dpB[i] = dpA[i + 1] + dpA[i + 2]; // A叫数字i的方案数 = B叫数字i+1的方案数 + B叫数字i+2的方案数 dpA[i] = dpB[i + 1] + dpB[i + 2]; } cout
免责声明:我们致力于保护作者版权,注重分享,被刊用文章因无法核实真实出处,未能及时与作者取得联系,或有版权异议的,请联系管理员,我们会立即处理! 部分文章是来自自研大数据AI进行生成,内容摘自(百度百科,百度知道,头条百科,中国民法典,刑法,牛津词典,新华词典,汉语词典,国家院校,科普平台)等数据,内容仅供学习参考,不准确地方联系删除处理! 图片声明:本站部分配图来自人工智能系统AI生成,觅知网授权图片,PxHere摄影无版权图库和百度,360,搜狗等多加搜索引擎自动关键词搜索配图,如有侵权的图片,请第一时间联系我们,邮箱:ciyunidc@ciyunshuju.com。本站只作为美观性配图使用,无任何非法侵犯第三方意图,一切解释权归图片著作权方,本站不承担任何责任。如有恶意碰瓷者,必当奉陪到底严惩不贷!