【算法之排序篇】 堆排序详解！(源码+图解)

文章目录

• 📑前言
• 🌤️堆的理论概念
• • ☁️堆的思想
  • 🌤️堆的代码具体实现
  • • ☁️图解
    • ☁️源码
    • ☁️源码剖析
    • 🌤️堆排序特性
    • • ☁️不稳定排序
      • ☁️时间复杂度
      • ☁️原地排序
      • ☁️不适用于小数据集
      • ☁️堆的构建和调整
      • ☁️适用于外部排序
      • ☁️稳定性
      • ☁️最好、最坏和平均情况
      • 🌤️全篇总结

        📑前言

        什么是堆排序？堆在原数据结构上是怎么实现堆排从而使数据有序的？

        🌤️堆的理论概念

        ☁️堆的思想

        堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。

        🌤️堆的代码具体实现

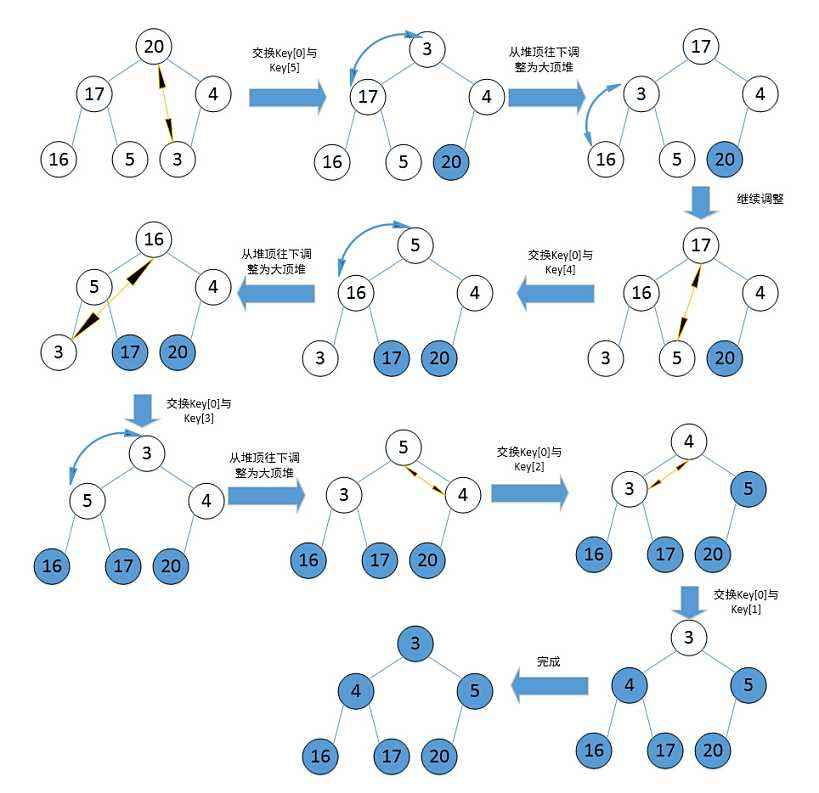
        ☁️图解

        

        ☁️源码

        //堆排序
        void AdjustDown(int* a, int n, int parent)
        {
        	int child = parent * 2 + 1;
        	while (child  a[child])
        		{
        			child++;
        		}
        		if (a[child] > a[parent])
        		{
        			Swap(&a[child], &a[parent]);
        			parent = child;
        			child = parent * 2 + 1;
        		}
        		else
        			break;
        	}
        }
        void HeapSort(int* a, int n)
        {
        	//升序(建大堆)  降序(建小堆)
        	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
        	{
        		AdjustDown(a, n, i);
        	}
        	int end = n - 1;
        	while (end > 0)
        	{
        		Swap(&a[0], &a[end]);
        		AdjustDown(a, end, 0);
        		end--;
        	}
        }
        

        ☁️源码剖析

        1. AdjustDown 函数用于维护堆的性质，即父节点的值大于或等于其子节点的值。它从一个节点开始，将它与其子节点比较，并交换它和较大子节点的值，然后继续向下递归调整，直到满足堆的性质。
        2. HeapSort 函数首先通过遍历数组，从最后一个非叶子节点开始，调用 函数，逐步构建最大堆。AdjustDown
        3. 然后，将堆的根节点（最大值）与数组的最后一个元素交换，将最大值放到正确的位置。
        4. 接着，重新调用 函数，将剩余元素重新构建成最大堆，排除已排序的部分。AdjustDown
        5. 重复步骤 3 和 4，直到整个数组有序。

        🌤️堆排序特性

        ☁️不稳定排序

        堆排序是一种不稳定的排序算法，因为在堆的调整过程中可能会改变相同值的元素的相对顺序。

        ☁️时间复杂度

        堆排序的平均和最坏时间复杂度均为 O(n*log(n))，其中 n 是待排序元素的数量。

        ☁️原地排序

        堆排序是一种原地排序算法，不需要额外的辅助存储空间，只需要在原数组上进行元素的交换和调整。

        ☁️不适用于小数据集

        堆排序的性能相对较好，但对于小规模的数据集来说，其常数项较大，不如快速排序等算法效率高。

        ☁️堆的构建和调整

        堆排序的核心是构建堆（通常是最大堆），然后反复将堆顶元素（最大值）与堆中的最后一个元素交换，并调整堆，使剩余部分仍然满足堆的性质。

        ☁️适用于外部排序

        堆排序也适用于外部排序问题，其中数据无法全部加载到内存中，需要逐块处理数据。

        ☁️稳定性

        堆排序通常不是稳定的排序算法，即相同值的元素在排序后的相对位置可能会改变。如果需要稳定性排序，应该选择其他算法，如归并排序。

        ☁️最好、最坏和平均情况

        堆排序的时间复杂度在任何情况下都是 O(n*log(n))，因此具有稳定的性能。

        🌤️全篇总结

        堆排序的主要优点在于它具有稳定的时间复杂度 O(n*log(n))，适用于大规模数据集的排序，而且是一种原地排序算法，不需要额外的空间。但它并不适用于小规模数据集，因为其常数项较大。堆排序也不是稳定排序，即相同值的元素在排序后的相对位置可能会改变。

        ☁️相信聪明的你肯定已经学会堆排了吧。

        看到这里希望给博主留个:👍点赞🌟收藏⭐️关注！

        你们的三连就是博主创作的最大动力！