Matlab——逻辑回归（原理、代码）
温馨提示：这篇文章已超过431天没有更新，请注意相关的内容是否还可用！
对于一个机器学习方法，通常由模型、策略和算法3个要素构成。
- 模型是假设空间的形式，如是线性函数还是条件概率；
- 策略是判断模型好坏的数学表达式，将学习问题转化为优化问题，一般策略对应一个代价函数（Cost Function）；
- 算法是上述优化问题的求解方法，有多种方法，如梯度下降法、直接求导、遗传算法等。
目录
1 逻辑回归原理
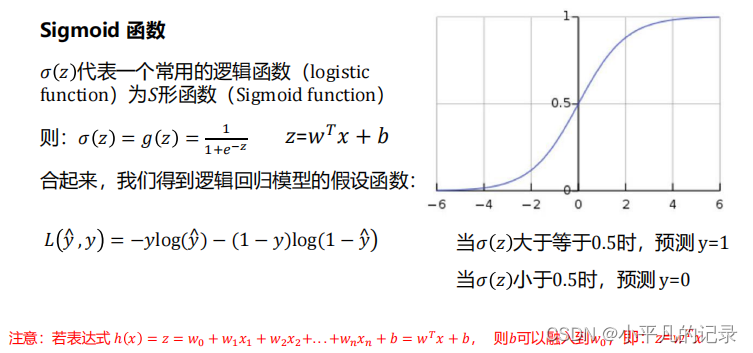
2 Sigmoid函数
3 逻辑回归理论公式推导
4 逻辑回归算法的改进——正则化
5 Matlab实践
1 逻辑回归原理
逻辑回归是一种广义的线性模型。虽然被称为回归，但在实际应用中常被用作分类，用于估计某个事件发生的概率。例如某用户购买商品的可能性，某病人患有某种疾病的可能性，某广告被用户点击的可能性等。
- 首先基于线性模型。若为了解决分类问题，需要把线性模型的输出做一个变换，利用Sigmoid函数，将实数域的输出映射到（0，1）区间，为输出提供了很好的概率解释。
- 其次策略方面，采用了交叉熵损失函数；
- 第三算法方面，为了最小化损失函数，采用了梯度下降方法。
2 Sigmoid函数
3 逻辑回归理论公式推导
——模型
其中p(y|x;w)是0-1分布（伯努利分布）。
——策略（定义损失函数）
求解w，定义一个指标衡量w的表现，即代价函数，利用最大似然法。
了衡量算法在全部训练样本上的表现如何，我们需要定义一个算法的代价函数，算法的代价函数是对𝑚个样本的损失函数求和然后除以𝑚（一般文献中）
——算法（梯度下降法）
α为迭代步长，
为假设集在第 i 个样本处的取值，
为真实的标签值。
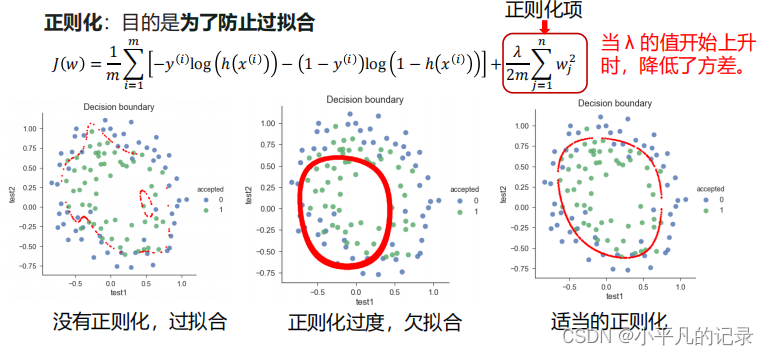
4 逻辑回归算法的改进——正则化
正则化，减少模型复杂度的一个方法。一般通过在目标函数上增加一个惩罚项。
这里是岭回归（Ridge Regression），对
范数
求导，得到梯度变化为：
一般通过
把系数消掉。
也将L2正则称为权重衰减。
5 Matlab实践
建模车辆里程数测试中出现问题的比例和车重量之间的关系。观测值包括车重、车的数量和损失的数量。
假设车辆损失数应该服从二项分布，最简单的想法是P（概率）和重量呈线性关系。
%% 原始数据 %一系列不同重量的车 weight = [2100 2300 2500 2700 2900 3100 3300 3500 3700 3900 4100 4300]'; %各个重量类型的车的数目 tested = [48 42 31 34 31 21 23 23 21 16 17 21]'; %每个重量的车辆在测试中fail掉的数目 failed = [1 2 0 3 8 8 14 17 19 15 17 21]'; %故障率 proportion = failed ./ tested; figure(1) plot(weight,proportion,'s') xlabel('重量');ylabel('比例');
散点数据
%% 线性拟合 %ployfit(x,y,n)执行多项式拟合，n代表多项式阶数，当n=1时，表示线性关系，返回多项式系数 linearCoef = polyfit(weight,proportion,1) %value = ployval(p,x)返回多项式的值，p是多项式系数，降序排列 linearFit = polyval(linearCoef,weight); figure(2) line2 = plot(weight,proportion,'s',weight,linearFit,'r-',[2000 4500],[0 0],'k:',[2000 4500],[1,1],'k:'); xlabel('重量');ylabel('比例'); set(gcf,'Position',[100 100 350 280]); set(gca,'FontSize',9); set(line2,'LineWidth',1.5)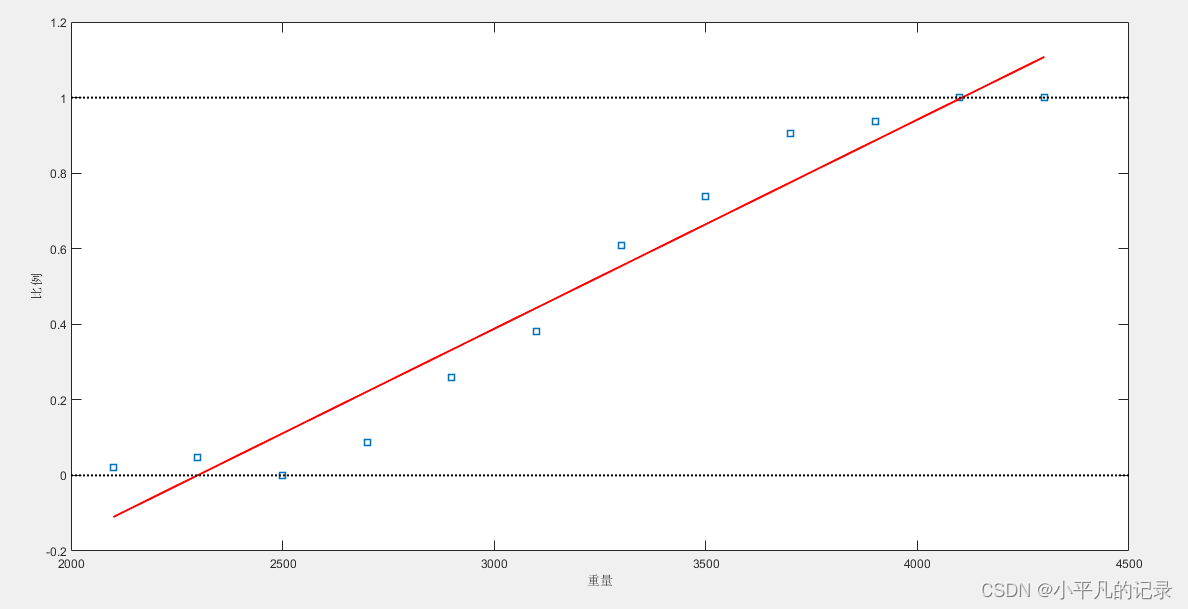
线性拟合
使用上述模型线性拟合，存在两个问题：
- 线性拟合会出现比例小于0或大于1的情况，而概率只能是[0,1]区间的数；
- 比例值不是正态分布的，违背了线性回归模型的假设条件。
下面使用高阶多项式看是否解决这些问题。
%% 多项式拟合 %区别在于这里选用3阶多项式，返回的stats是一个结构体，作为polyval函数的输入 %可用于误差估计，ctr包含了均值和方差，可用于对输入x归一化 [cubicCoef,stats,ctr] = polyfit(weight,proportion,3) cubicFit = polyval(cubicCoef,weight,[ ],ctr); %利用归一化的weight进行多项式拟合 figure(3) line = plot(weight,proportion,'s',weight,cubicFit,'r-',[2000 4500],[0 0],'k:',[2000 4500],[1,1],'k:'); xlabel('重量');ylabel('比例'); set(gcf,'Position',[100 100 350 280]); set(gca,'FontSize',9); set(line,'LineWidth',1.5)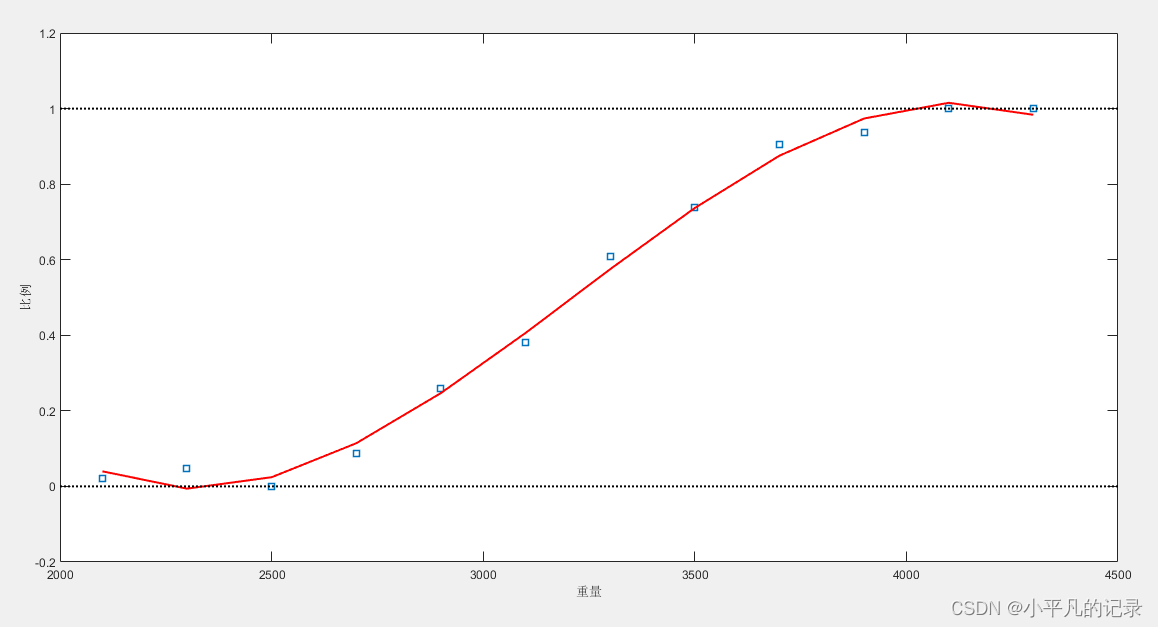
多项式拟合
此模型仍存在问题。
- 当车辆重量超过4000时，比例开始下降，当重量继续增加时，比例可能下降到0以下。
- 正态分布的假设依然不合理。
利用glmfit拟合一个Logistic回归模型，其优于线性回归模型的两点：
- Logistic回归中的Sigmoid函数将输出值限制在[0,1]之间，符合此例问题情况；
- Logistic回归采用的拟合方法适用于二项分布。
%% glmfit拟合 % 在glmfit中一般response是一个列向量，但是当分布是二项分布时，y可以是一个二值向量， % 表示单次观测中成功还是失败，也可以是一个两列的矩阵，第一列表示成功的次数（目标出现的次数）， % 第二列表示总共的观测次数，因此这里y=[failed,tested] % 另外指定distri='binomal',link='logit' [logitCoef1,dev1] = glmfit(weight,[failed tested],'binomial','logit'); % glmval用于测试拟合的模型，计算出估计的y值 logitFit = glmval(logitCoef1,weight,'logit'); figure(4) line3 = plot(weight,proportion,'bs',weight,logitFit,'r-'); xlabel('重量');ylabel('比例'); set(gcf,'Position',[100 100 350 280]); set(gca,'FontSize',9); set(line3,'LineWidth',1.5) legend('数据','logistics回归')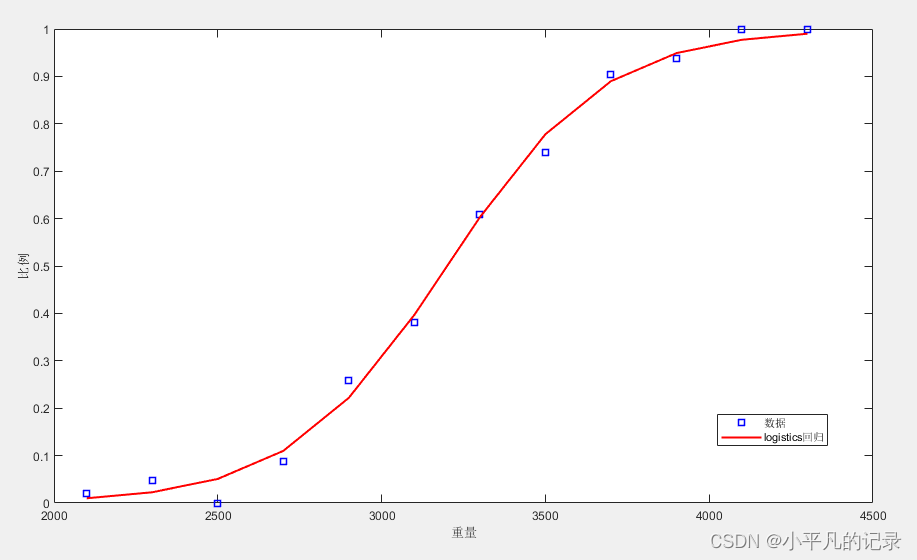
Logistics回归
上述主要利用广义线性模型实现Logistic回归。
当重量太小或太大时，故障率要么无限接近0，要么无限接近1，且曲线很好地刻画了数据点的分布，故而为一个合理的模型。
下面进行预测。
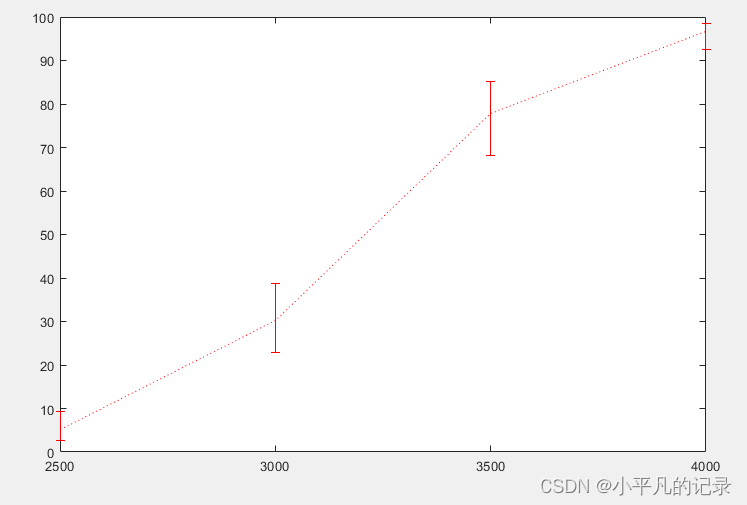
%% 预测 [logitCoef,dev,stats] = glmfit(weight,[failed tested],'binomial','logit'); normplot(stats.residp); weightPred = 2500:500:4000; % dlo和dhi是置信区间的下限和上限 [failedPred,dlo,dhi] = glmval(logitCoef,weightPred,'logit',stats,0.95,100); figure(5) line = errorbar(weightPred,failedPred,dlo,dhi,'r:');
预测误差图
当车的重量为3000时，测试中出现故障的车辆数约为30.2辆，
有95%的概率会有（30.2-7.3，30.2+8.4）辆车出现故障。
Python参考：
机器学习练习2-逻辑回归_YukinoPon的博客-CSDN博客
https://www.cnblogs.com/Qiao-Q/p/16837426.html
sklearn-逻辑回归_sklearn逻辑回归_CHEN的小喵的博客-CSDN博客
