自动驾驶控制算法——车辆动力学模型

车辆动力学模型（2自由度模型）

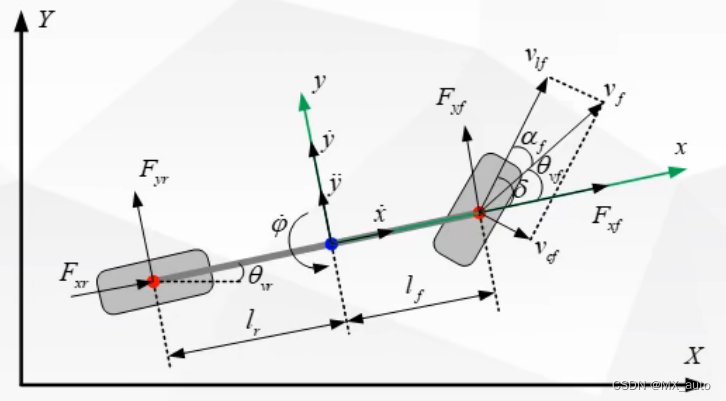
考虑车辆 y 方向和绕 z 轴的旋转，可以得到车辆2自由度模型，如下图：

m a y = F y f + F y r (2.1) ma_y = F_{yf} + F_{yr} \tag{2.1} may​=Fyf​+Fyr​(2.1)

I z ψ ¨ = l f F y f − l r F y r (2.2) I_z\ddot\psi = l_fF_{yf} - l_rF_{yr} \tag{2.2} Iz​ψ¨​=lf​Fyf​−lr​Fyr​(2.2)

经验公式可知，轮胎侧向力和速度偏角成正比，前后各两个轮胎，故有（根据轮胎坐标系有关符号定义可知，正的侧偏力产生负的侧偏角，因此侧偏刚度为负值。不同坐标系的定义可能不同，Apollo中侧偏刚度系数为正值，相应的状态方程也会有所改变，因此，这里与apollo保持一致，侧偏刚度采用正值）：

F y f = 2 C α f ( δ − θ v f ) F y r = 2 C α r ( − θ v r ) (2.3) F_{yf} = 2C_{\alpha f}(\delta-\theta_{vf}) \\ F_{yr} = 2C_{\alpha r}(-\theta_{vr}) \tag{2.3} Fyf​=2Cαf​(δ−θvf​)Fyr​=2Cαr​(−θvr​)(2.3)

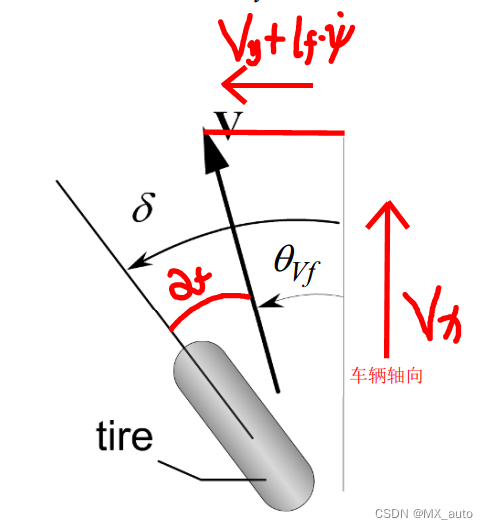
再参考图四可得:

tan ⁡ ( θ v f ) = V y + l f ψ ˙ V x tan ⁡ ( θ v r ) = V y − l r ψ ˙ V x (2.4) \tan(\theta_{vf}) = \frac{V_y + l_f\dot{\psi}}{V_x} \\ \tan(\theta_{vr}) = \frac{V_y - l_r\dot{\psi}}{V_x} \tag{2.4} tan(θvf​)=Vx​Vy​+lf​ψ˙​​tan(θvr​)=Vx​Vy​−lr​ψ˙​​(2.4)

在小角度转向假设下，可以将上述公式转换为：

θ v f = V y + l f ψ ˙ V x θ v r = V y − l r ψ ˙ V x (2.5) \theta_{vf} = \frac{V_y + l_f\dot{\psi}}{V_x} \\ \theta_{vr} = \frac{V_y - l_r\dot{\psi}}{V_x} \tag{2.5} θvf​=Vx​Vy​+lf​ψ˙​​θvr​=Vx​Vy​−lr​ψ˙​​(2.5)

上述公式中：

• F f y F_{fy} Ffy​ 和 F f r F_{fr} Ffr​ – 前轮横向力和后轮横向力
• C α f C_{\alpha f} Cαf​ 和 C α r C_{\alpha r} Cαr​ – 前轮侧偏刚度和后轮侧偏刚度（采用正值）
• θ v f \theta_{vf} θvf​ 和 θ v r \theta_{vr} θvr​ – 前轮速度偏角和后轮速度偏角
• a y a_y ay​ – 侧向加速度（等于 y 方向加速度和向心加速度之和，即 a y = y ¨ + V x ψ ˙ a_y = \ddot{y} + V_x \dot{\psi} ay​=y¨​+Vx​ψ˙​）
• V y = y ˙ V_y = \dot{y} Vy​=y˙​ – 车辆y方向速度
• m – 车辆质量
• I z I_z Iz​ – 绕Z轴转动惯量

  将式 ( 2.3 , 2.4 , 2.5 ) (2.3,2.4,2.5) (2.3,2.4,2.5)带入公式 ( 2.1 ) (2.1) (2.1):

  m a y = m ( y ¨ + V x ψ ˙ ) = F y f + F y r = 2 C α f ( δ f − θ v f ) + 2 C α r ( − θ v r ) = 2 C α f ( δ f − V y + l f ψ ˙ V x ) + 2 C α r ( − V y − l r ψ ˙ V x ) (2.6) ma_y = m(\ddot{y} + V_x \dot{\psi}) = F_{yf} + F_{yr} = 2C_{\alpha f}(\delta_f-\theta_{vf}) + 2C_{\alpha r}(-\theta_{vr}) = 2C_{\alpha f}(\delta_f-\frac{V_y + l_f\dot{\psi}}{V_x}) + 2C_{\alpha r}(-\frac{V_y - l_r\dot{\psi}}{V_x}) \tag{2.6} may​=m(y¨​+Vx​ψ˙​)=Fyf​+Fyr​=2Cαf​(δf​−θvf​)+2Cαr​(−θvr​)=2Cαf​(δf​−Vx​Vy​+lf​ψ˙​​)+2Cαr​(−Vx​Vy​−lr​ψ˙​​)(2.6)

  整理得到横向加速度公式：

  y ¨ = − 2 C α f + 2 C α r m V x y ˙ + ( − V x − 2 C α f l f − 2 C α r l r m V x ) ψ ˙ + 2 C α f m δ f (2.7) \ddot{y} = -\frac{2C_{\alpha f} + 2C_{\alpha r}}{mV_x} \dot{y} + (-V_x-\frac{2C_{\alpha f} l_f - 2C_{\alpha r} l_r}{mV_x})\dot{\psi} + \frac{2C_{\alpha f}}{m}\delta_f \tag{2.7} y¨​=−mVx​2Cαf​+2Cαr​​y˙​+(−Vx​−mVx​2Cαf​lf​−2Cαr​lr​​)ψ˙​+m2Cαf​​δf​(2.7)

  将式 ( 2.3 , 2.4 , 2.5 ) (2.3,2.4,2.5) (2.3,2.4,2.5)带入公式 ( 2.2 ) (2.2) (2.2):

  I z ψ ¨ = l f 2 C α f ( δ f − θ v f ) − l r 2 C α r ( − θ v r ) = l f 2 C α f ( δ f − V y + l f ψ ˙ V x ) − l r 2 C α r ( − V y − l r ψ ˙ V x ) (2.8) I_z\ddot{\psi} = l_f 2C_{\alpha f}(\delta_f-\theta_{vf}) - l_r 2C_{\alpha r}(-\theta_{vr}) = l_f 2C_{\alpha f}(\delta_f-\frac{V_y + l_f\dot{\psi}}{V_x}) - l_r 2C_{\alpha r}(-\frac{V_y - l_r\dot{\psi}}{V_x}) \tag{2.8} Iz​ψ¨​=lf​2Cαf​(δf​−θvf​)−lr​2Cαr​(−θvr​)=lf​2Cαf​(δf​−Vx​Vy​+lf​ψ˙​​)−lr​2Cαr​(−Vx​Vy​−lr​ψ˙​​)(2.8)

  整理得到横摆角加速度公式：

  ψ ¨ = − ( 2 l f C α f − 2 l r C α r V x I z ) y ˙ + ( − 2 l f 2 C α f + 2 l r 2 C α r V x I z ) ψ ˙ + 2 l f C α f I z δ f (2.9) \ddot{\psi} = -(\frac{2 l_f C_{\alpha f} - 2 l_r C_{\alpha r}}{V_x I_z}) \dot{y} + (-\frac{2 l_f^2 C_{\alpha f} + 2 l_r^2 C_{\alpha r}}{V_x I_z}) \dot{\psi} + \frac{2 l_f C_{\alpha f}}{I_z}\delta_f \tag{2.9} ψ¨​=−(Vx​Iz​2lf​Cαf​−2lr​Cαr​​)y˙​+(−Vx​Iz​2lf2​Cαf​+2lr2​Cαr​​)ψ˙​+Iz​2lf​Cαf​​δf​(2.9)

  将式 2.7 2.7 2.7和 2.9 2.9 2.9写成矩阵形式，得到车辆动力学模型（与apollo保持一致，侧偏刚度采用正值）：

  d d t { y y ˙ ψ ψ ˙ } = [ 0 1 0 0 0 − 2 C α f + 2 C α r m V x 0 − V x − 2 C α f l f − 2 C α r l r m V x 0 0 0 1 0 − 2 l f C α f − 2 l r C α r V x I z 0 − 2 l f 2 C α f + 2 l r 2 C α r V x I z ] { y y ˙ ψ ψ ˙ } + { 0 2 C α f m 0 2 l f C α f I z } δ f (2.10) \frac{d}{dt} \left\{ \begin{matrix} y \\ \dot{y} \\ \psi \\ \dot{\psi} \end{matrix} \right\} = \left[ \begin{matrix} 0 & 1 & 0 & 0 \\ 0 & -\frac{2C_{\alpha f} + 2C_{\alpha r}}{mV_x} & 0 & -V_x-\frac{2C_{\alpha f} l_f - 2C_{\alpha r} l_r}{mV_x} \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{2 l_f C_{\alpha f} - 2 l_r C_{\alpha r}}{V_x I_z} & 0 & -\frac{2 l_f^2 C_{\alpha f} + 2 l_r^2 C_{\alpha r}}{V_x I_z} \\ \end{matrix} \right] \left\{ \begin{matrix} y \\ \dot{y} \\ \psi \\ \dot{\psi} \end{matrix} \right\} + \left\{ \begin{matrix} 0 \\ \frac{2C_{\alpha f}}{m} \\ 0 \\ \frac{2 l_f C_{\alpha f}}{I_z} \end{matrix} \right\} \delta_f \tag{2.10} dtd​⎩ ⎨ ⎧​yy˙​ψψ˙​​⎭ ⎬ ⎫​= ​0000​1−mVx​2Cαf​+2Cαr​​0−Vx​Iz​2lf​Cαf​−2lr​Cαr​​​0000​0−Vx​−mVx​2Cαf​lf​−2Cαr​lr​​1−Vx​Iz​2lf2​Cαf​+2lr2​Cαr​​​ ​⎩ ⎨ ⎧​yy˙​ψψ˙​​⎭ ⎬ ⎫​+⎩ ⎨ ⎧​0m2Cαf​​0Iz​2lf​Cαf​​​⎭ ⎬ ⎫​δf​(2.10)

  基于车辆动力学的道路-车辆误差模型

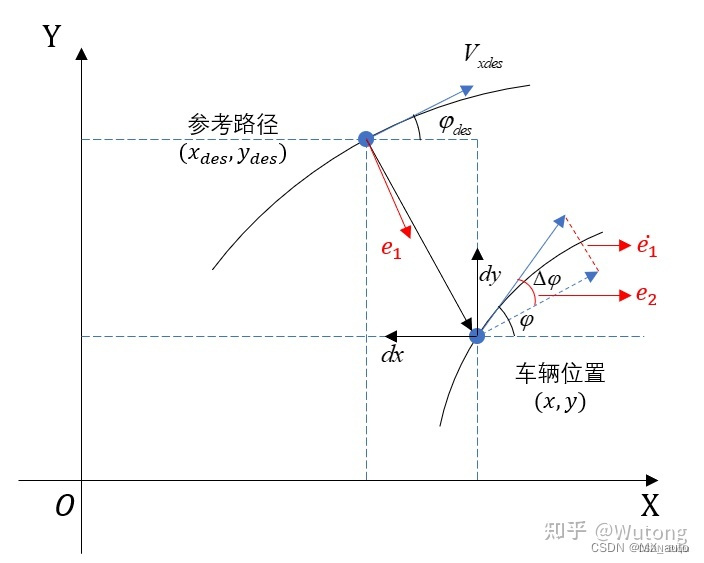
  要实现自动驾驶车辆的横向控制系统，首先要建立车辆质心相对于车道中心线的位置和航向误差模型，示意图如下所示：

  

  其中：

  • e 1 e_1 e1​ – 横向位置偏差（横向位置偏差）
  • e 1 ˙ \dot{e_1} e1​˙​ – 横向偏差变化率（横向速度偏差）
  • e 1 ¨ \ddot{e_1} e1​¨​ – 横向偏差变化率的变化率（横向加速度偏差）
  • e 2 e_2 e2​ – 航向角偏差
  • e 2 ˙ \dot{e_2} e2​˙​ – 航向角偏差变化率
  • e 2 ¨ \ddot{e_2} e2​¨​ – 航向角偏差变化率的变化率
  • V x V_x Vx​ – 车辆沿轴线方向速度
  • ϕ \phi ϕ – 道路横向坡度
  • ψ d e s ˙ \dot{\psi_{des}} ψdes​˙​ – （路径参考点理论横摆角速度）车辆参考航向变化率， V x R \frac{V_x}{R} RVx​​
  • ψ d e s ¨ \ddot{\psi_{des}} ψdes​¨​ – （路径参考点理论横摆角加速度）车辆参考航向变化率的导数， V x 2 R = V x ψ d e s ˙ \frac{V_x^2}{R}=V_x \dot{\psi_{des}} RVx2​​=Vx​ψdes​˙​

    首先根据定义容易得到如下公式：

    e 2 = ψ − ψ d e s e_2 = \psi - \psi_{des} e2​=ψ−ψdes​

    e 2 ˙ = ψ ˙ − ψ d e s ˙ \dot{e_2} = \dot{\psi} - \dot{\psi_{des}} e2​˙​=ψ˙​−ψdes​˙​

    e 2 ¨ = ψ ¨ − ψ d e s ¨ \ddot{e_2} = \ddot{\psi} - \ddot{\psi_{des}} e2​¨​=ψ¨​−ψdes​¨​

    根据定义可以得到：

    e 1 ¨ = a y − a y d e s = ( y ¨ + ψ ˙ V x ) − ψ d e s ˙ V x = y ¨ + V x ( ψ ˙ − ψ d e s ˙ ) = y ¨ + V x e 2 ˙ \begin{aligned} \ddot{e_1} & = a_y - a_{ydes} \\ & = (\ddot{y} + \dot{\psi}V_x) - \dot{\psi_{des}}V_x \\ & = \ddot{y} + V_x(\dot{\psi} - \dot{\psi_{des}}) \\ & = \ddot{y} + V_x\dot{e_2} \end{aligned} e1​¨​​=ay​−aydes​=(y¨​+ψ˙​Vx​)−ψdes​˙​Vx​=y¨​+Vx​(ψ˙​−ψdes​˙​)=y¨​+Vx​e2​˙​​

    假设纵向速度 V x V_x Vx​不变，可以进一步推导出：

    e 1 ˙ = y ˙ + V x e 2 \dot{e_1} = \dot{y} + V_xe_2 e1​˙​=y˙​+Vx​e2​

    将公式转换形式为：

    y ˙ = e 1 ˙ − V x e 2 \dot{y} = \dot{e_1} - V_xe_2 y˙​=e1​˙​−Vx​e2​

    y ¨ = e 1 ¨ − V x e 2 ˙ \ddot{y} = \ddot{e_1} - V_x\dot{e_2} y¨​=e1​¨​−Vx​e2​˙​

    ψ ˙ = e 2 ˙ + ψ d e s ˙ \dot{\psi} = \dot{e_2} + \dot{\psi_{des}} ψ˙​=e2​˙​+ψdes​˙​

    ψ ¨ = e 2 ¨ + ψ d e s ¨ \ddot{\psi} = \ddot{e_2} + \ddot{\psi_{des}} ψ¨​=e2​¨​+ψdes​¨​

    整理公式可以得到横向位置误差变化率的导数：

    e 1 ¨ = − 2 C α f + 2 C α r m V x e 1 ˙ + 2 C α f + 2 C α r m V x V x e 2 − 2 C α f l f − 2 C α r l r m V x e 2 ˙ − ( V x + 2 C α f l f − 2 C α r l r m V x ) ψ d e s ˙ + 2 C α f m δ (2.11) \ddot{e_1} = -\frac{2C_{\alpha f} + 2C_{\alpha r}} {mV_x} \dot{e_1} + \frac{2C_{\alpha f} + 2C_{\alpha r}} {mV_x} V_xe_2 - \frac{2C_{\alpha f} l_f - 2C_{\alpha r} l_r}{mV_x} \dot{e_2} - (V_x + \frac{2C_{\alpha f} l_f - 2C_{\alpha r} l_r}{mV_x}) \dot{\psi_{des}} + \frac{2C_{\alpha f}}{m}\delta \tag{2.11} e1​¨​=−mVx​2Cαf​+2Cαr​​e1​˙​+mVx​2Cαf​+2Cαr​​Vx​e2​−mVx​2Cαf​lf​−2Cαr​lr​​e2​˙​−(Vx​+mVx​2Cαf​lf​−2Cαr​lr​​)ψdes​˙​+m2Cαf​​δ(2.11)

    整理公式可以得到航向误差变化率的导数：

    e 2 ¨ = − ( 2 l f C α f − 2 l r C α r V x I z ) e 1 ˙ + 2 l f C α f − 2 l r C α r V x I z V x e 2 + ( − 2 l f 2 C α f + 2 l r 2 C α r V x I z ) e 2 ˙ − 2 l f 2 C α f + 2 l r 2 C α r V x I z ψ d e s ˙ − ψ d e s ¨ + 2 l f C α f I z δ (2.12) \ddot{e_2} = -(\frac{2 l_f C_{\alpha f} - 2 l_r C_{\alpha r}}{V_x I_z}) \dot{e_1} + \frac{2 l_f C_{\alpha f} - 2 l_r C_{\alpha r}}{V_x I_z} V_xe_2 + (-\frac{2 l_f^2 C_{\alpha f} + 2 l_r^2 C_{\alpha r}}{V_x I_z}) \dot{e_2} -\frac{2 l_f^2 C_{\alpha f} + 2 l_r^2 C_{\alpha r}}{V_x I_z} \dot{\psi_{des}} - \ddot{\psi_{des}} + \frac{2 l_f C_{\alpha f}}{I_z}\delta \tag{2.12} e2​¨​=−(Vx​Iz​2lf​Cαf​−2lr​Cαr​​)e1​˙​+Vx​Iz​2lf​Cαf​−2lr​Cαr​​Vx​e2​+(−Vx​Iz​2lf2​Cαf​+2lr2​Cαr​​)e2​˙​−Vx​Iz​2lf2​Cαf​+2lr2​Cαr​​ψdes​˙​−ψdes​¨​+Iz​2lf​Cαf​​δ(2.12)

    取 X = [ e 1 , e 1 ˙ , e 2 , e 2 ˙ ] T X=[e_1,\dot{e_1},e_2,\dot{e_2}]^T X=[e1​,e1​˙​,e2​,e2​˙​]T为误差状态变量，则道路-车辆误差状态方程可写成（与apollo保持一致，侧偏刚度采用正值）：

    X ˙ = A X + B U + B 1 ψ d e s ˙ + B 2 ψ d e s ¨ + C d d t [ e 1 e 1 ˙ e 2 e 2 ˙ ] = [ 0 1 0 0 0 − 2 C α f + 2 C α r m V x 2 C α f + 2 C α r m − 2 C α f l f − 2 C α r l r m V x 0 0 0 1 0 − 2 l f C α f − 2 l r C α r V x I z 2 l f C α f − 2 l r C α r I z − 2 l f 2 C α f + 2 l r 2 C α r V x I z ] [ e 1 e 1 ˙ e 2 e 2 ˙ ] + [ 0 2 C α f m 0 2 l f C α f I z ] δ + [ 0 − V x − 2 C α f l f − 2 C α r l r m V x 0 − 2 l f 2 C α f + 2 l r 2 C α r V x I z ] ψ d e s ˙ + [ 0 0 0 − 1 ] ψ d e s ¨ + [ 0 g 0 0 ] sin ⁡ ϕ (2.13) \dot{X}=AX+BU+B_1 \dot{\psi_{des}} +B_2 \ddot{\psi_{des}}+C \\ \frac{d}{dt}\left[\begin{matrix} e_1 \\ \dot{e_1} \\ e_2 \\ \dot{e_2} \end{matrix}\right] =\left[\begin{matrix} 0 & 1 & 0 & 0 \\ 0 & -\frac{2C_{\alpha f} + 2C_{\alpha r}} {mV_x} & \frac{2C_{\alpha f} + 2C_{\alpha r}} {m} & - \frac{2C_{\alpha f} l_f - 2C_{\alpha r} l_r}{mV_x}\\ 0 & 0 & 0 & 1 \\ 0 & -\frac{2 l_f C_{\alpha f} - 2 l_r C_{\alpha r}}{V_x I_z} & \frac{2 l_f C_{\alpha f} - 2 l_r C_{\alpha r}}{I_z} & -\frac{2 l_f^2 C_{\alpha f} + 2 l_r^2 C_{\alpha r}}{V_x I_z} \end{matrix} \right] \left[ \begin{matrix} e_1 \\ \dot{e_1} \\ e_2 \\ \dot{e_2} \end{matrix} \right] +\left[ \begin{matrix} 0 \\ \frac{2C_{\alpha f}}{m} \\ 0 \\ \frac{2 l_f C_{\alpha f}}{I_z}\end{matrix}\right]\delta+\left[\begin{matrix} 0 \\- V_x - \frac{2C_{\alpha f} l_f - 2C_{\alpha r} l_r}{mV_x} \\ 0 \\ -\frac{2 l_f^2 C_{\alpha f} + 2 l_r^2 C_{\alpha r}}{V_x I_z} \end{matrix} \right] \dot{\psi_{des}}+\left[\begin{matrix} 0 \\ 0 \\ 0 \\ -1 \end{matrix} \right] \ddot{\psi_{des}} +\left[\begin{matrix} 0 \\ g \\ 0 \\ 0 \end{matrix} \right] \sin{\phi} \tag{2.13} X˙=AX+BU+B1​ψdes​˙​+B2​ψdes​¨​+Cdtd​ ​e1​e1​˙​e2​e2​˙​​ ​= ​0000​1−mVx​2Cαf​+2Cαr​​0−Vx​Iz​2lf​Cαf​−2lr​Cαr​​​0m2Cαf​+2Cαr​​0Iz​2lf​Cαf​−2lr​Cαr​​​0−mVx​2Cαf​lf​−2Cαr​lr​​1−Vx​Iz​2lf2​Cαf​+2lr2​Cαr​​​ ​ ​e1​e1​˙​e2​e2​˙​​ ​+ ​0m2Cαf​​0Iz​2lf​Cαf​​​ ​δ+ ​0−Vx​−mVx​2Cαf​lf​−2Cαr​lr​​0−Vx​Iz​2lf2​Cαf​+2lr2​Cαr​​​ ​ψdes​˙​+ ​000−1​ ​ψdes​¨​+ ​0g00​ ​sinϕ(2.13)

    其中：

    A = [ 0 1 0 0 0 − 2 C α f + 2 C α r m V x 2 C α f + 2 C α r m − 2 C α f l f − 2 C α r l r m V x 0 0 0 1 0 − 2 l f C α f − 2 l r C α r V x I z 2 l f C α f − 2 l r C α r I z − 2 l f 2 C α f + 2 l r 2 C α r V x I z ] ， B = [ 0 2 C α f m 0 2 l f C α f I z ] A = \left[ \begin{matrix} 0 & 1 & 0 & 0 \\ 0 & -\frac{2C_{\alpha f} + 2C_{\alpha r}} {mV_x} & \frac{2C_{\alpha f} + 2C_{\alpha r}} {m} & - \frac{2C_{\alpha f} l_f - 2C_{\alpha r} l_r}{mV_x}\\ 0 & 0 & 0 & 1 \\ 0 & -\frac{2 l_f C_{\alpha f} - 2 l_r C_{\alpha r}}{V_x I_z} & \frac{2 l_f C_{\alpha f} - 2 l_r C_{\alpha r}}{I_z} & -\frac{2 l_f^2 C_{\alpha f} + 2 l_r^2 C_{\alpha r}}{V_x I_z} \end{matrix} \right]， B =\left[ \begin{matrix} 0 \\ \frac{2C_{\alpha f}}{m} \\ 0 \\ \frac{2 l_f C_{\alpha f}}{I_z} \end{matrix} \right] A= ​0000​1−mVx​2Cαf​+2Cαr​​0−Vx​Iz​2lf​Cαf​−2lr​Cαr​​​0m2Cαf​+2Cαr​​0Iz​2lf​Cαf​−2lr​Cαr​​​0−mVx​2Cαf​lf​−2Cαr​lr​​1−Vx​Iz​2lf2​Cαf​+2lr2​Cαr​​​ ​，B= ​0m2Cαf​​0Iz​2lf​Cαf​​​ ​

    B 1 = [ 0 − V x − 2 C α f l f − 2 C α r l r m V x 0 − 2 l f 2 C α f + 2 l r 2 C α r V x I z ] , B 2 = [ 0 0 0 − 1 ] , C = [ 0 g 0 0 ] sin ⁡ ϕ , U = δ B_1 =\left[\begin{matrix} 0 \\- V_x - \frac{2C_{\alpha f} l_f - 2C_{\alpha r} l_r}{mV_x} \\ 0 \\ -\frac{2 l_f^2 C_{\alpha f} + 2 l_r^2 C_{\alpha r}}{V_x I_z} \end{matrix} \right], B_2 = \left[ \begin{matrix} 0 \\ 0 \\ 0 \\ -1 \end{matrix} \right], C= \left[ \begin{matrix} 0 \\ g \\ 0 \\ 0\end{matrix}\right] \sin{\phi}, U = \delta B1​= ​0−Vx​−mVx​2Cαf​lf​−2Cαr​lr​​0−Vx​Iz​2lf2​Cαf​+2lr2​Cαr​​​ ​,B2​= ​000−1​ ​,C= ​0g00​ ​sinϕ,U=δ

    这里仅仅考虑了横向的动力学关系，如果需要同时考虑到纵向动力学，且忽略最后带 ψ d e s ¨ \ddot{\psi_{des}} ψdes​¨​项和横坡度 C C C项，可以将上式进一步扩展为：

    d d t [ e 1 e 1 ˙ e 2 e 2 ˙ e 3 e 3 ˙ ] = [ 0 1 0 0 0 0 0 − 2 C α f + 2 C α r m V x 2 C α f + 2 C α r m − 2 C α f l f − 2 C α r l r m V x 0 0 0 0 0 1 0 0 0 − 2 l f C α f − 2 l r C α r V x I z 2 l f C α f − 2 l r C α r I z − 2 l f 2 C α f + 2 l r 2 C α r V x I z 0 0 0 0 0 0 0 1 0 0 0 0 0 0 ] [ e 1 e 1 ˙ e 2 e 2 ˙ e 3 e 3 ˙ ] + [ 0 0 2 C α f m 0 0 0 2 l f C α f I z 0 0 0 0 − 1 ] [ δ a ] + [ 0 − V x − 2 C α f l f − 2 C α r l r m V x 0 − 2 l f 2 C α f + 2 l r 2 C α r V x I z 0 0 ] ψ d e s ˙ (2.14) \frac{d}{dt} \left[ \begin{matrix} e_1 \\ \dot{e_1} \\ e_2 \\ \dot{e_2} \\ e_3 \\ \dot{e_3} \end{matrix} \right] =\left[ \begin{matrix} 0 & 1 & 0 & 0 &0 & 0\\ 0 & -\frac{2C_{\alpha f} + 2C_{\alpha r}} {mV_x} & \frac{2C_{\alpha f} + 2C_{\alpha r}} {m} & - \frac{2C_{\alpha f} l_f - 2C_{\alpha r} l_r}{mV_x} &0 &0 \\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & -\frac{2 l_f C_{\alpha f} - 2 l_r C_{\alpha r}}{V_x I_z} & \frac{2 l_f C_{\alpha f} - 2 l_r C_{\alpha r}}{I_z} & -\frac{2 l_f^2 C_{\alpha f} + 2 l_r^2 C_{\alpha r}}{V_x I_z} & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0\\ \end{matrix} \right] \left[ \begin{matrix} e_1 \\ \dot{e_1} \\ e_2 \\ \dot{e_2} \\ e_3 \\ \dot{e_3} \end{matrix} \right] +\left[ \begin{matrix} 0 & 0 \\ \frac{2C_{\alpha f}}{m} & 0\\ 0 & 0 \\ \frac{2 l_f C_{\alpha f}}{I_z} & 0 \\ 0 & 0 \\ 0 & -1 \end{matrix} \right] \left[ \begin{matrix} \delta \\ a \end{matrix} \right] + \left[ \begin{matrix} 0 \\- V_x - \frac{2C_{\alpha f} l_f - 2C_{\alpha r} l_r}{mV_x} \\ 0 \\ -\frac{2 l_f^2 C_{\alpha f} + 2 l_r^2 C_{\alpha r}}{V_x I_z} \\ 0 \\0 \end{matrix} \right] \dot{\psi_{des}} \tag{2.14} dtd​ ​e1​e1​˙​e2​e2​˙​e3​e3​˙​​ ​= ​000000​1−mVx​2Cαf​+2Cαr​​0−Vx​Iz​2lf​Cαf​−2lr​Cαr​​00​0m2Cαf​+2Cαr​​0Iz​2lf​Cαf​−2lr​Cαr​​00​0−mVx​2Cαf​lf​−2Cαr​lr​​1−Vx​Iz​2lf2​Cαf​+2lr2​Cαr​​00​000000​000010​ ​ ​e1​e1​˙​e2​e2​˙​e3​e3​˙​​ ​+ ​0m2Cαf​​0Iz​2lf​Cαf​​00​00000−1​ ​[δa​]+ ​0−Vx​−mVx​2Cαf​lf​−2Cαr​lr​​0−Vx​Iz​2lf2​Cαf​+2lr2​Cαr​​00​ ​ψdes​˙​(2.14)

    其中:

    • e 3 e_3 e3​ – 纵向位置偏差
    • e 3 ˙ \dot{e_3} e3​˙​ – 纵向速度偏差（纵向位置偏差变化率）
    • e 3 ¨ \ddot{e_3} e3​¨​ – 纵向加速度偏差（纵向速度偏差变化率）
    • a a a – 加速度补偿量

      动力学误差模型离散化

      连续系统的离散化方法比较多，例如正向/反向差分变化法，双线性变换法，脉冲响应不变法，阶跃响应不变法等。

      上述部分基于车辆横向误差和航向误差的动力学模型建立后，需要对模型进行离散化，这里对系统矩阵A进行中点欧拉离散化，对B和C矩阵进行正向差分变换，可以得到离散模型。下面对下列连续状态空间方程进行离散化：

      连续状态空间方程(忽略最后带 ψ d e s ¨ \ddot{\psi_{des}} ψdes​¨​项和横坡度 C C C项)：

      X ˙ = A X + B U + B 1 ψ d e s ˙ \dot{X} = AX + BU + B_1\dot{\psi_{des}} X˙=AX+BU+B1​ψdes​˙​

      系统矩阵 A 双线性变换离散后为：

      A d = ( I − T 2 A ) − 1 ( I + T 2 A ) A_d = (I - \frac{T}{2}A)^{-1}(I + \frac{T}{2}A) Ad​=(I−2T​A)−1(I+2T​A)

      B d = B ∗ T B_d = B*T Bd​=B∗T

      B 1 d = B 1 ∗ T B_{1d} = B_1*T B1d​=B1​∗T

      则离散后的模型为:

      X ( k + 1 ) = A d X ( k ) + B d U ( k ) + B 1 d ∗ ψ d e s ˙ ( k ) X(k+1) = A_d X(k) + B_d U(k) + B_{1d}*\dot{\psi_{des}}(k) X(k+1)=Ad​X(k)+Bd​U(k)+B1d​∗ψdes​˙​(k)

      注：

      • I I I 为单位矩阵
      • T T T 为采样周期
      • 忽略最后一项 ψ d e s ¨ \ddot{\psi_{des}} ψdes​¨​
      • U ( k ) = [ δ ( k ) , a ( k ) ] T U(k) = [\delta(k), a(k)]^T U(k)=[δ(k),a(k)]T