PyTorch张量创建和随机数生成器算法

07-19 1608阅读

文章目录

1、基本创建方式

1.1、根据已有数据创建张量
1.2、根据已有数据创建张量
1.3、根据已有数据创建张量
2、创建线性和随机张量

2.1、创建线性空间的张量
2.2、创建随机张量
2.3、什么是随机数种子
2.4、initial_seed()和manual_seed()
3、创建01张量

3.1、全0张量
3.2、全1张量
3.3、指定张量
4、张量元素类型转换⭐
5、随机数生成器的算法⭐

5.1、线性同余生成器LCG
5.2、梅森旋转算法
5.3、Xorshift算法

5.4、其他算法

🍃作者介绍：双非本科大三网络工程专业在读，阿里云专家博主，专注于Java领域学习，擅长web应用开发、数据结构和算法，初步涉猎人工智能和前端开发。

🦅个人主页：@逐梦苍穹

📕所属专栏：人工智能

🌻gitee地址：xzl的人工智能代码仓库

✈ 您的一键三连，是我创作的最大动力🌹

1、基本创建方式

torch.tensor：根据指定数据创建张量
torch.Tensor：根据形状创建张量, 其也可用来创建指定数据的张量
torch.IntTensor、torch.FloatTensor、torch.DoubleTensor 创建指定类型的张量

1.1、根据已有数据创建张量

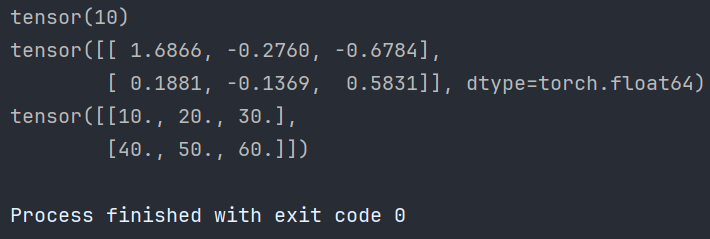
# 1. 根据已有数据创建张量
def test01():
    # 1. 创建张量标量
    data = torch.tensor(10)
    print(data)
    # 2. numpy 数组, 由于 data 为 float64, 下面代码也使用该类型
    data = np.random.randn(2, 3)
    data = torch.tensor(data)
    print(data)
    # 3. 列表, 下面代码使用默认元素类型 float32
    data = [[10., 20., 30.], [40., 50., 60.]]
    data = torch.tensor(data)
    print(data)

1.2、根据已有数据创建张量

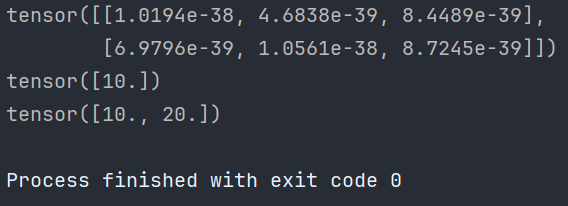
# 2. 创建指定形状的张量
def test02():
    # 1. 创建2行3列的张量, 默认 dtype 为 float32
    data = torch.Tensor(2, 3)
    print(data)
    # 2. 注意: 如果传递列表, 则创建包含指定元素的张量
    data = torch.Tensor([10])
    print(data)
    data = torch.Tensor([10, 20])
    print(data)

1.3、根据已有数据创建张量

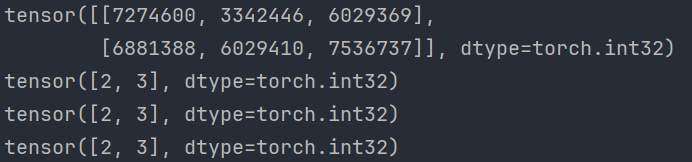
# 3. 使用具体类型的张量
def test03():
    # 1. 创建2行3列, dtype 为 int32 的张量
    data = torch.IntTensor(2, 3)
    print(data)
    # 2. 注意: 如果传递的元素类型不正确, 则会进行类型转换
    # TODO 警告信息如下:
    #   DeprecationWarning: an integer is required (got type float).
    #   Implicit conversion to integers using __int__ is deprecated,
    #   and may be removed in a future version of Python
    # 解决方式：①显示处理; ②用torch.tensor()来指定数据类型
    data = torch.IntTensor([2.5, 3.3])
    data2 = torch.IntTensor([int(2.5), int(3.3)])
    data3 = torch.tensor([2, 3], dtype=torch.int32)
    print(data)
    print(data2)
    print(data3)
    # 3. 其他的类型
    data = torch.ShortTensor()  # int16
    data = torch.LongTensor()  # int64
    data = torch.FloatTensor()  # float32
    data = torch.DoubleTensor()  # float64

2、创建线性和随机张量

torch.arange 和 torch.linspace：创建线性张量
torch.random.initial_seed 和 torch.random.manual_seed：随机种子设置
torch.randn：创建随机张量

线性张量通常是指按顺序生成的张量，例如等差数列
随机张量是指元素值是随机数的张量

类型	方法	示例代码	代码解释
线性张量	torch.linspace	linear_tensor = torch.linspace(0, 10, steps=5)	创建一个从0到10的包含5个元素的线性张量。
	torch.arange	linear_tensor = torch.arange(0, 10, step=2)	创建一个从0到10（不包括10），步长为2的线性张量。
随机张量	torch.rand	random_tensor = torch.rand(2, 3)	创建一个2x3的随机张量，元素均匀分布在[0, 1)区间。
	torch.randn	random_tensor = torch.randn(2, 3)	创建一个2x3的随机张量，元素服从标准正态分布
	torch.randint	random_tensor = torch.randint(0, 10, (2, 3))	创建一个2x3的随机整数张量，元素值在[0, 10)之间。
	torch.randperm	random_tensor = torch.randperm(10)	创建一个从0到9的随机排列张量。

2.1、创建线性空间的张量

# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/7/15 0:31
import torch
# 1. 创建线性空间的张量
def test01():
    # 1. 在指定区间按照步长生成元素 [start, end, step)
    data = torch.arange(0, 10, 2)
    print(data)
    # 2. 在指定区间按照元素个数生成
    data = torch.linspace(0, 11, 10)
    print(data)

2.2、创建随机张量

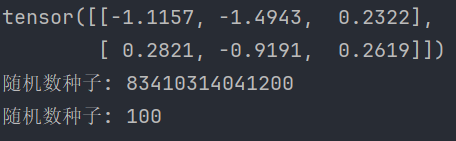
# 2. 创建随机张量
def test02():
    # 1. 创建随机张量
    data = torch.randn(2, 3)  # 创建2行3列张量
    print(data)
    # 2. 随机数种子设置
    print('随机数种子:', torch.random.initial_seed())
    torch.random.manual_seed(100)
    print('随机数种子:', torch.random.initial_seed())

2.3、什么是随机数种子

随机数种子（Random Seed）是用于初始化随机数生成器的一个整数值。

随机数生成器是通过算法生成一系列看似随机的数字，但这些数字实际上是确定的，只要种子相同，每次生成的随机数序列也相同

随机数种子的作用：

确保可重复性：通过设置相同的随机数种子，可以确保每次运行程序时生成相同的随机数序列。这对于调试和实验非常重要，因为它允许研究人员和开发人员重现实验结果，从而验证和比较不同算法的性能。
调试和测试：在开发和调试过程中，设置随机数种子可以帮助定位和解决问题。固定种子后，如果程序出现问题，研究人员可以重现同样的条件进行调试。
实验的一致性：在机器学习和深度学习实验中，设置相同的随机数种子可以确保每次训练模型时的初始条件一致，从而使得实验结果具有可比性。
多次运行的一致性：在需要多次运行实验以取平均值或进行统计分析时，设置相同的种子可以确保每次运行的条件一致，从而减少实验结果的方差。

总结：

随机数种子是用于初始化随机数生成器的整数值。
作用：
1. 确保程序的可重复性。
2. 帮助调试和测试。
3. 保证实验结果的一致性和可比性。
4. 在多次运行实验时保持条件一致。

2.4、initial_seed()和manual_seed()

torch.random.initial_seed 和 torch.random.manual_seed 的区别：

torch.random.initial_seed函数返回的是PyTorch启动时的随机种子（seed）。这个种子是在PyTorch加载时自动设置的，并且是全局的，通常在PyTorch启动时随机生成
torch.random.manual_seed函数用于显式地设置随机种子，以确保结果的可重复性。通过设置相同的种子，可以确保每次运行时生成相同的随机数序列，这在调试和实验中非常有用。

3、创建01张量

torch.ones 和 torch.ones_like 创建全1张量
torch.zeros 和 torch.zeros_like 创建全0张量
torch.full 和 torch.full_like 创建全为指定值张量

3.1、全0张量

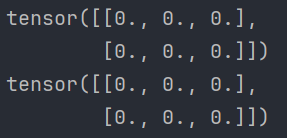
def test01():
    # 1. 创建指定形状全0张量
    data = torch.zeros(2, 3)
    print(data)
    # 2. 根据张量形状创建全0张量
    data = torch.zeros_like(data)
    print(data)

3.2、全1张量

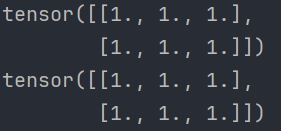
def test02():
    # 1. 创建指定形状全0张量
    data = torch.ones(2, 3)
    print(data)
    # 2. 根据张量形状创建全0张量
    data = torch.ones_like(data)
    print(data)

3.3、指定张量

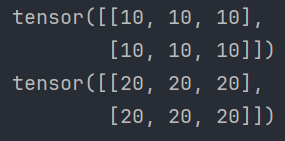
def test03():
    # 1. 创建指定形状指定值的张量
    data = torch.full([2, 3], 10)
    print(data)
    # 2. 根据张量形状创建指定值的张量
    data = torch.full_like(data, 20)
    print(data)

4、张量元素类型转换⭐

tensor.type(torch.DoubleTensor)：将张量显式转换为指定的类型。
torch.double()：将张量转换为双精度浮点数

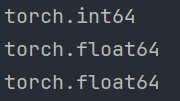
# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/7/15 2:13
import torch
def test():
    # 指定张量
    data = torch.full([2, 3], 10)
    print(data.dtype)
    # 将 data 元素类型转换为 float64 类型
    # 1. 第一种方法
    data = data.type(torch.DoubleTensor)
    print(data.dtype)
    # 转换为其他类型
    # data = data.type(torch.ShortTensor)
    # data = data.type(torch.IntTensor)
    # data = data.type(torch.LongTensor)
    # data = data.type(torch.FloatTensor)
    
    # 2. 第二种方法
    data = data.double()
    print(data.dtype)
    # 转换为其他类型
    # data = data.short()
    # data = data.int()
    # data = data.long()
    # data = data.float()

输出：

5、随机数生成器的算法⭐

随机数种子（Random Seed）是用于初始化随机数生成器的一个整数值。

下面介绍常见伪随机数生成算法

5.1、线性同余生成器LCG

线性同余生成器（Linear Congruential Generator, LCG）

这是最早的伪随机数生成器之一，生成的随机数序列由以下递归关系定义：

[ X n + 1 = ( a X n + c ) m o d m ] [ X_{n+1} = (aX_n + c) \mod m ] [Xn+1=(aXn+c)modm]

参数含义

( X ) ( X ) (X)是生成的伪随机数序列。
( X n ) ( X_n ) (Xn) 表示当前的随机数。
( X n + 1 ) ( X_{n+1} ) (Xn+1) 表示下一个随机数。
( a ) ( a ) (a)是乘数（multiplier），通常选择为一个大整数。
( c ) ( c ) (c)是增量（increment），也是一个整数。
( m ) ( m ) (m)是模数（modulus），表示随机数的范围，通常是一个大整数。
( X 0 ) ( X_0 ) (X0)是初始种子（seed），这是随机数生成的起点。
计算步骤
1. 选择参数：确定乘数 ( a ) ( a ) (a)、增量 ( c ) ( c ) (c)、模数 ( m ) ( m ) (m)和初始种子 ( X 0 ) ( X_0 ) (X0)。
2. 计算下一个随机数：使用公式 ( X n + 1 = ( a X n + c ) m o d m ) ( X_{n+1} = (aX_n + c) \mod m ) (Xn+1=(aXn+c)modm)计算下一个随机数。
3. 循环生成：将 ( X n + 1 ) ( X_{n+1} ) (Xn+1)作为新的当前随机数，重复步骤2，生成所需数量的随机数。
优缺点

**优点：**简单且易于实现。
**缺点：**周期性强，产生的随机数质量较低。

5.2、梅森旋转算法

梅森旋转算法（Mersenne Twister）

梅森旋转算法是现代最常用的伪随机数生成算法之一，特别适合科学计算和仿真。

梅森旋转算法得名于它的周期长度，特别是 ( 2 19937 − 1 ) (2^{19937} - 1) (219937−1)，这是一个梅森素数。

其具体实现较为复杂，以下是简化的描述：
1. 状态向量：算法维护一个状态向量，包含624个32位整数。
2. 初始化：
  1. 使用一个种子值初始化状态向量。
  2. 常用初始化方法为：
    [ state [ 0 ] = seed ] [ \text{state}[0] = \text{seed} ] [state[0]=seed]
    [ state [ i ] = ( f ⋅ ( state [ i − 1 ] ⊕ ( state [ i − 1 ] ≫ ( w − 2 ) ) ) ) + i ] [\text{state}[i] = (f \cdot (\text{state}[i-1] \oplus (\text{state}[i-1] \gg (w-2)))) + i] [state[i]=(f⋅(state[i−1]⊕(state[i−1]≫(w−2))))+i]
3. 生成随机数：
  - 算法每次生成624个随机数，并存储在状态向量中。
  - 当所有624个数都被使用后，再次生成新的624个数。
  - 旋转和混合：
    - 生成新随机数的核心步骤是将状态向量旋转，并进行一系列混合操作以确保高质量的随机性。
    - 具体操作包括提取、变换和混合部分位数。
优点：长周期，良好的统计特性。
缺点：比较复杂，初始化时间较长。

两个公式解释：
① [ state [ 0 ] = seed ] [ \text{state}[0] = \text{seed} ] [state[0]=seed]

state 是一个数组，用于存储梅森旋转算法的内部状态。
这个公式表示用给定的 seed（种子）值来初始化 state 数组的第一个元素。
seed 是算法的初始输入，它确定了随机数生成器的起点。

② [ state [ i ] = ( f ⋅ ( state [ i − 1 ] ⊕ ( state [ i − 1 ] ≫ ( w − 2 ) ) ) ) + i ] [\text{state}[i] = (f \cdot (\text{state}[i-1] \oplus (\text{state}[i-1] \gg (w-2)))) + i] [state[i]=(f⋅(state[i−1]⊕(state[i−1]≫(w−2))))+i]

这个公式用于初始化 state 数组的后续元素，i 从1到623（共624个元素）。
s t a t e [ i ] state[i] state[i]：数组 state 的第 i 个元素。
f f f：常数值 1812433253，用于混合操作。
s t a t e [ i − 1 ] state[i−1] state[i−1]：数组 state 的第 i-1 个元素，即前一个元素。
⊕ ⊕ ⊕：按位异或操作。
≫ ≫ ≫：算术右移操作。
w w w：字长，通常是32。
s t a t e [ i − 1 ] ≫ ( w − 2 ) state[i−1]≫(w−2) state[i−1]≫(w−2)：将 state[i-1] 向右移 w-2 位。
最后的 + i 是将当前的索引值 i 加到结果中。

5.3、Xorshift算法

Xorshift是一种基于异或操作的高效伪随机数生成器。

该算法使用一系列移位和异或操作生成随机数。

优点：快速，适合嵌入式系统。
缺点：周期相对较短，随机数质量依赖于具体实现。

5.4、其他算法

其他常见的伪随机数生成算法还包括：
- Lehmer随机数生成器：也是一种线性同余生成器，但参数选择得更好。
- PCG（Permuted Congruential Generator）：新的伪随机数生成器，具有良好的统计特性和性能。

VPS购买请点击我