利用Vivado和MATLAB分别设计FIR滤波器并滤除高频正弦波

一、利用MATLAB实现滤波

1.设计要求

（1）在MATLAB中，调用Filter Design & Analysis Tools工具，产生一个低通滤波器，以16bits定点量化滤波器系数，并产生XILINX的COE文件。

（2）在MATLAB中，产生两个正弦信号，数据位宽16bits，频率分别为3MHz和19MHz，数据长度为4096点。两个正弦信号合路（相加），送入该低通滤波器中，观察其输出信号。

2.任务一：设计滤波器

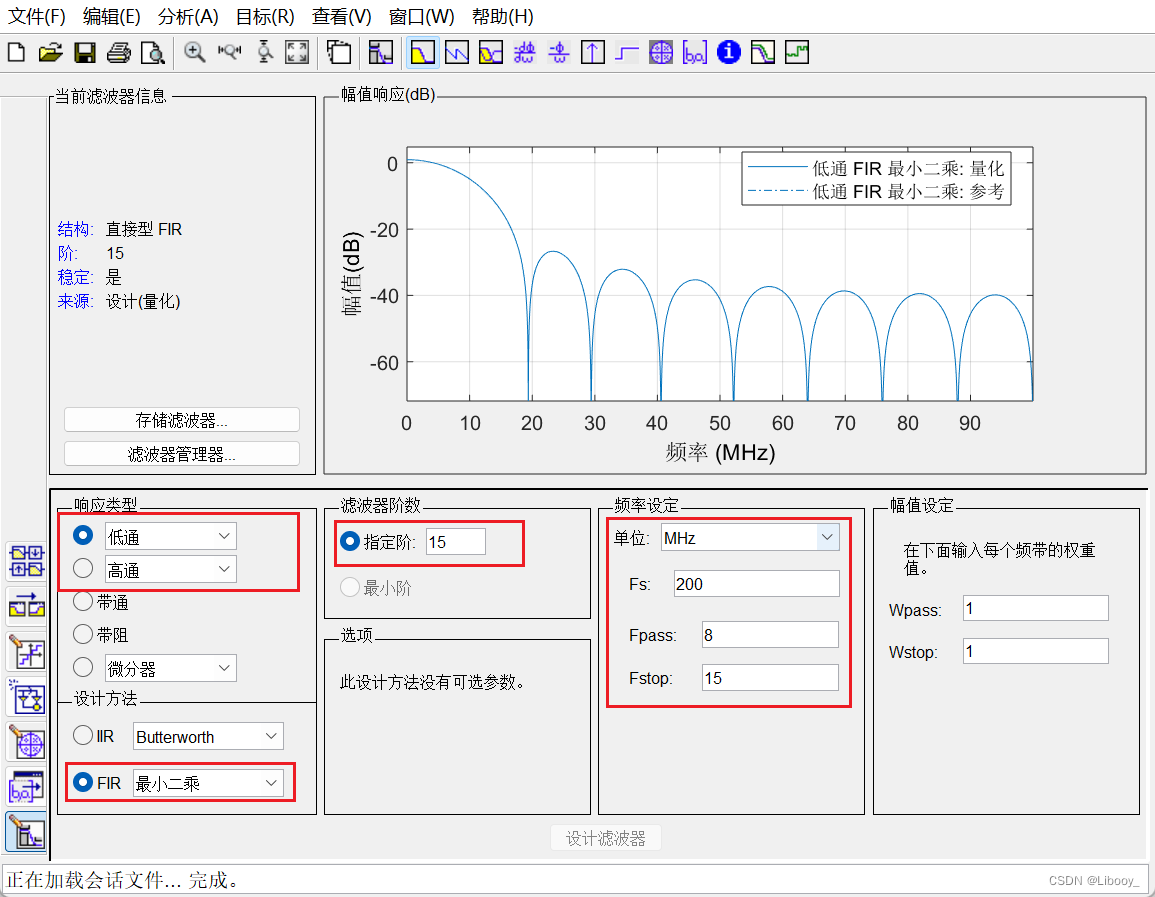
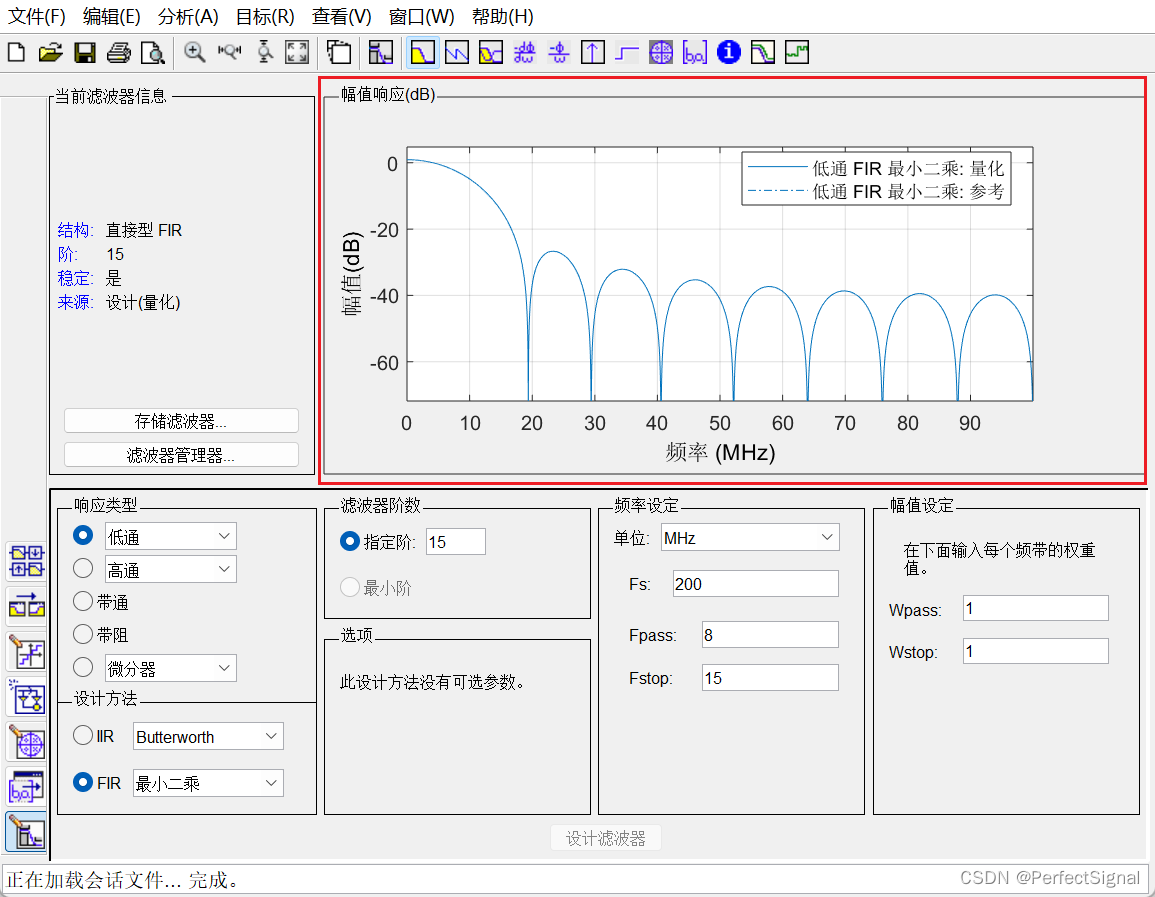
（1）在MATLAB中选择APP-滤波器设计工具，滤波器参数设置如下：

由于两路正弦波分别为3MHz和19MHz，所以将滤波器的通带截止频率设置为8MHz，将阻带开始频率设置为15MHz。

滤波器的采样频率应该大于信号最高频率的两倍，即38MHz，本文中取200MHz。注意：在Vivado中，FIR ip核的采样频率也要设置为200MHz，两处需要统一。

一般来说，数字滤波器的阶数越高，其复杂度越高，滤波器带内越平滑，具体取值取多少应在工程中取舍，本文中取15。

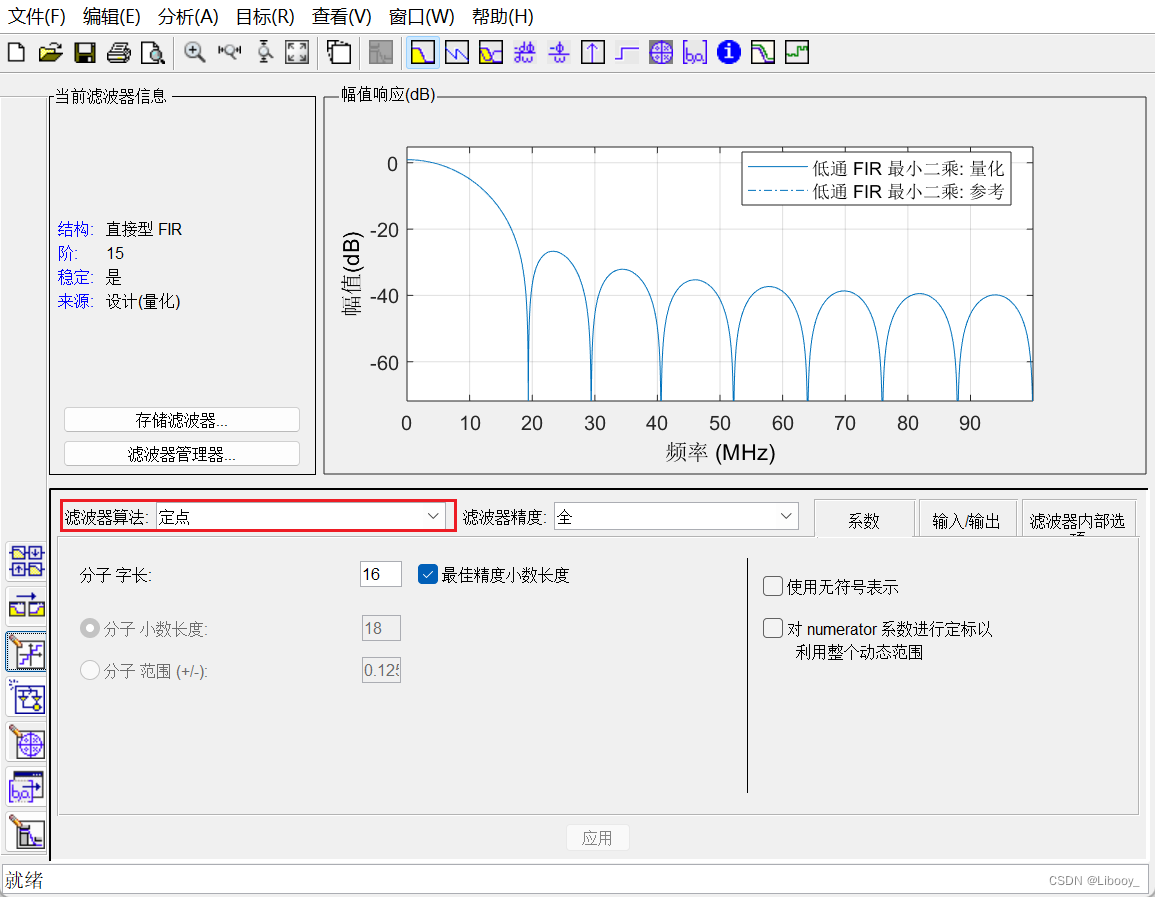
（2）点击左侧第三个小图标：设置量化参数，将滤波器算法指定为定点，将字长设置为16（由设计要求可知）。

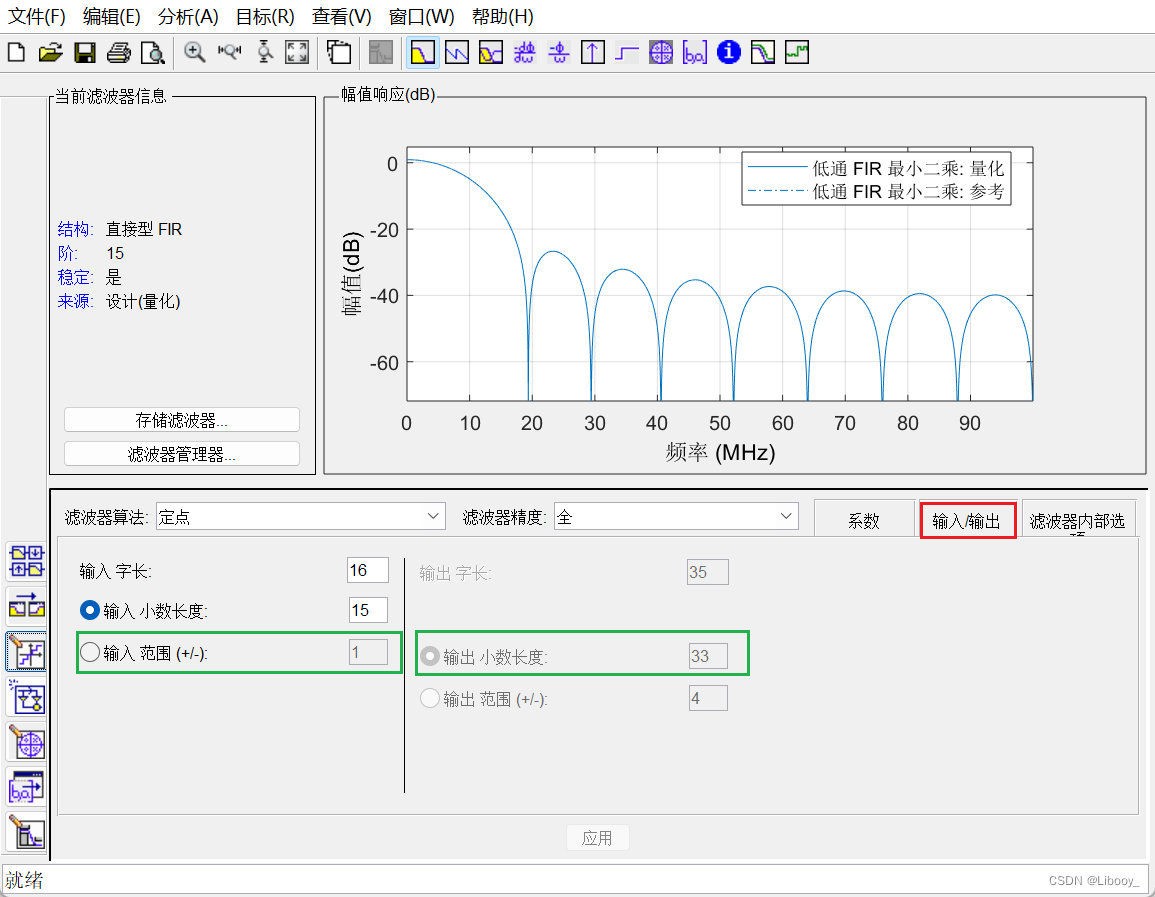
点击输入/输出，可以看到该滤波器的输入范围是[-1,1]，输出小数长度是33。在后续输入时要注意信号的范围，如果不在要求的范围内会出错。

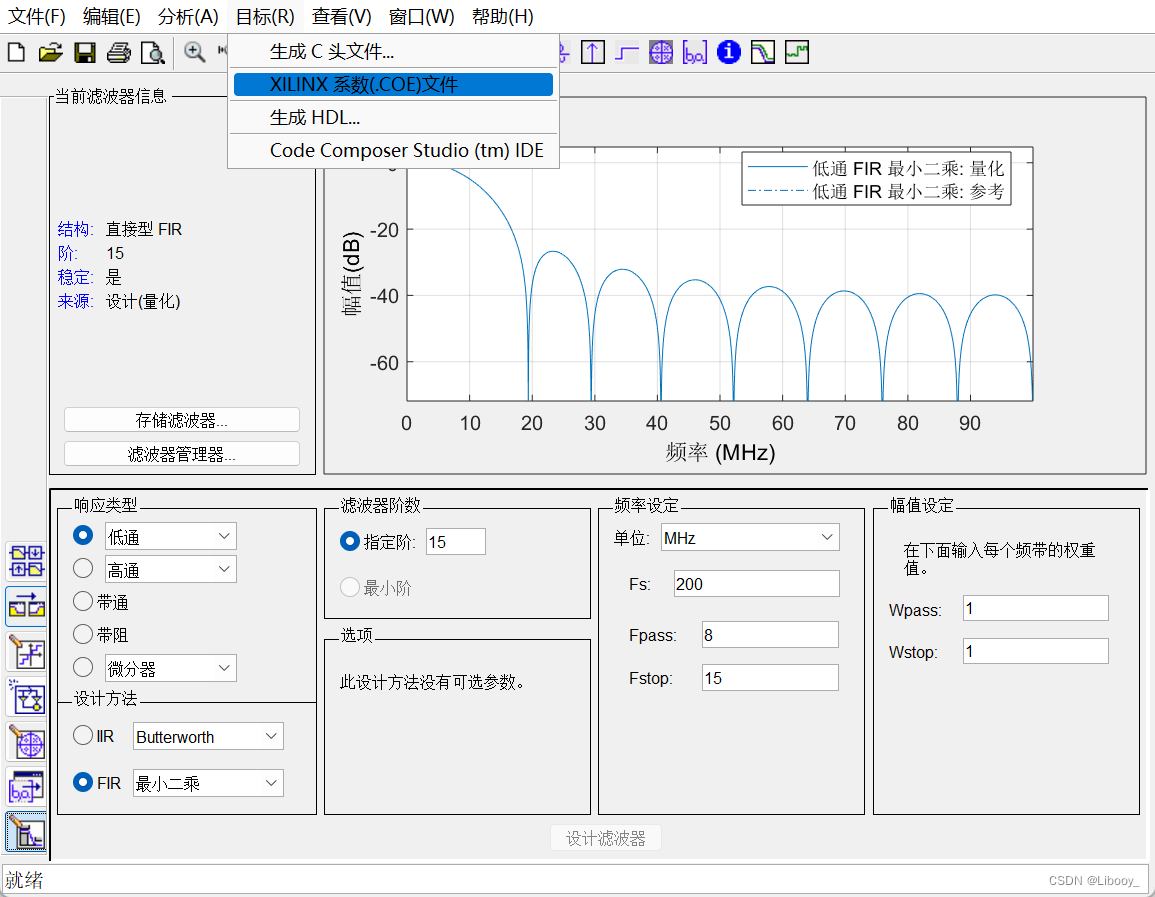
（3）点击任务栏目标-XILINX系数(.COE)文件，保存至相应目录下，后续在Vivoda中设置ip核时需要导入。

2.任务二

（1）代码

clc
clear all
close all
%% 生成两个正弦信号
depth = 4096;   % 存储器的单元数4096
widths = 16;    % 数据宽度为16位
Fs = 200e6;     % 采样频率为200MHz
t = 0:1/Fs:(4096-1)/Fs; % 时间向量
f1 = 3e6;       % 第一个正弦信号频率为3MHz
f2 = 19e6;      % 第二个正弦信号频率为19MHz
signal1 = sin(2*pi*f1*t)+1;  
signal2 = sin(2*pi*f2*t)+1; 
%% 合并两个信号
combined_signal = (signal1 + signal2)/4;
%% 调用低通滤波器设计函数
Hd = lowpass_filter;
%% 对合并信号进行滤波
filtered_signal = filter(Hd, combined_signal);
%% 绘制所有信号
figure;
subplot(4,1,1);
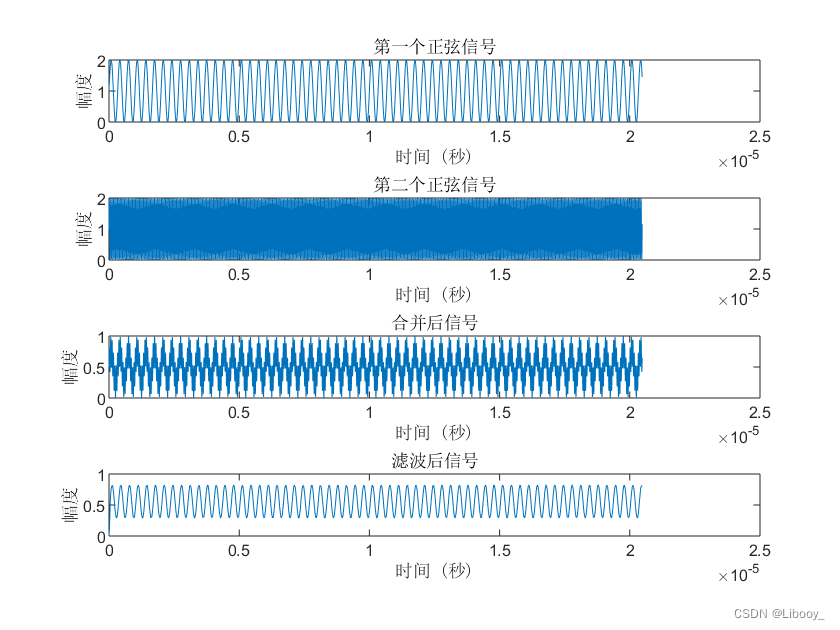
plot(t, double(signal1));
title('第一个正弦信号','Fontname','SimSun');
xlabel('时间 (秒)','Fontname','SimSun');
ylabel('幅度','Fontname','SimSun');
subplot(4,1,2);
plot(t, double(signal2));
title('第二个正弦信号','Fontname','SimSun');
xlabel('时间 (秒)','Fontname','SimSun');
ylabel('幅度','Fontname','SimSun');
subplot(4,1,3);
plot(t, double(combined_signal));
title('合并后信号','Fontname','SimSun');
xlabel('时间 (秒)','Fontname','SimSun');
ylabel('幅度','Fontname','SimSun');
subplot(4,1,4);
plot(t, double(filtered_signal));
title('滤波后信号','Fontname','SimSun');
xlabel('时间 (秒)','Fontname','SimSun');
ylabel('幅度','Fontname','SimSun');

上文中提到，滤波器的输入范围为[-1,1]，所以需要将合路信号变换到[-1,1]，这里选择先给两路信号加上幅值为1的直流分量,此时合路信号的范围为[0,4]，再除以4，即[0,1]，符合滤波器输入要求。这样做的原因在于：后续需要通过MATLAB产生正弦波数据表ROM，为了后续在Vivado中计算方便，产生时将信号扩大，并且添加了直流分量将信号搬移为正值，为了统一输入，此处做同样处理，即添加直流分量。

（2）结果

由图1-5可知，滤波后的信号频率与3MHz信号频率基本相同，但是幅值发生了变化，这是因为滤波器的幅度响应不是常数，所以3MHz的信号也有所衰减。

二、利用Vivado实现滤波

1.设计要求

（1）在Vivado软件中，采用FIR Compiler进行配置，并输入MATLAB产生的滤波器系数，产生一个低通滤波器。

（2）在Vivado软件中，产生一个正弦信号表：一个完整的正弦信号周期，共4096个点，精度为16bits，以ROM方式存放。

（3）例化两个正弦信号ROM，通过控制地址的步进量的方式，产生两个正弦信号输出，频率近似为3MHz和19MHz。

（4）两个正弦信号相加后，输入低通滤波器中，在Modelsim软件中，以HDL仿真方式观察其输出信号。

2.任务三：设计FIR

（1）IP核设置

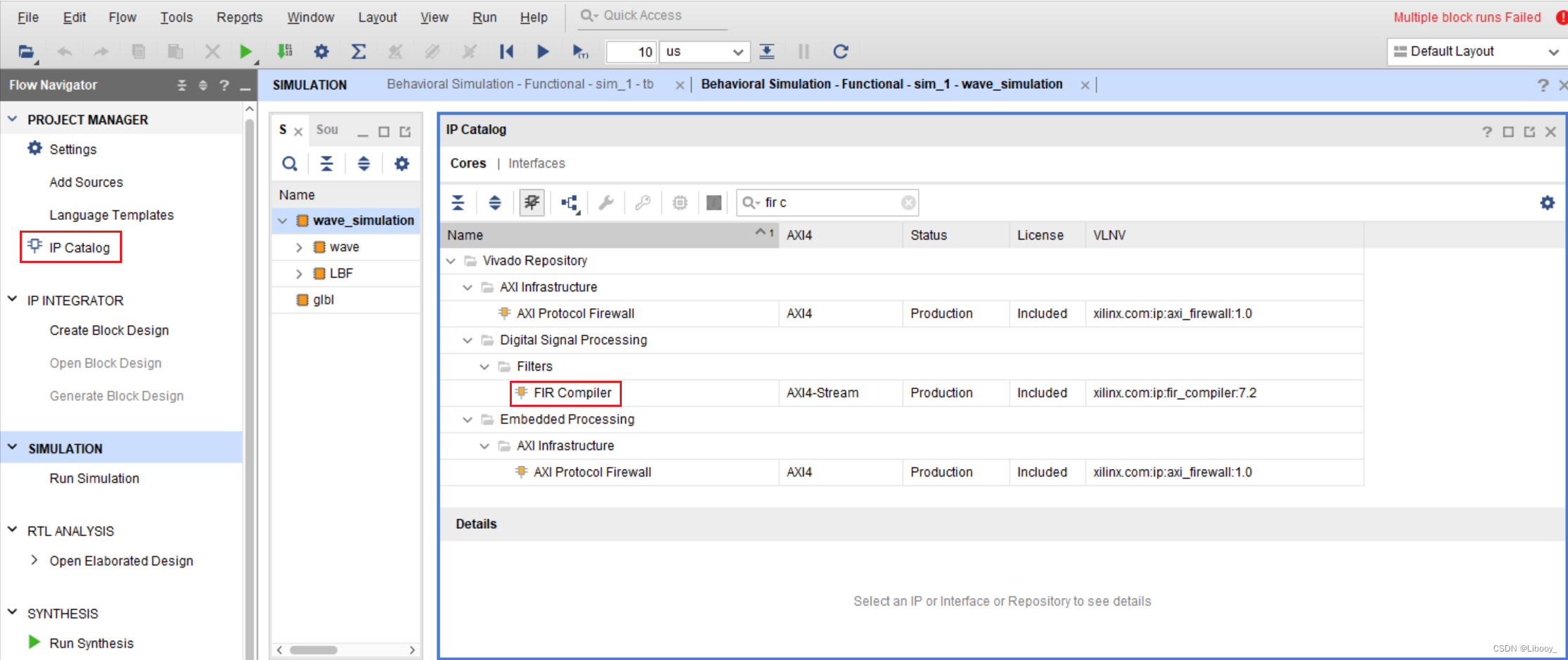
①选择IP Catalog-FIR Compile

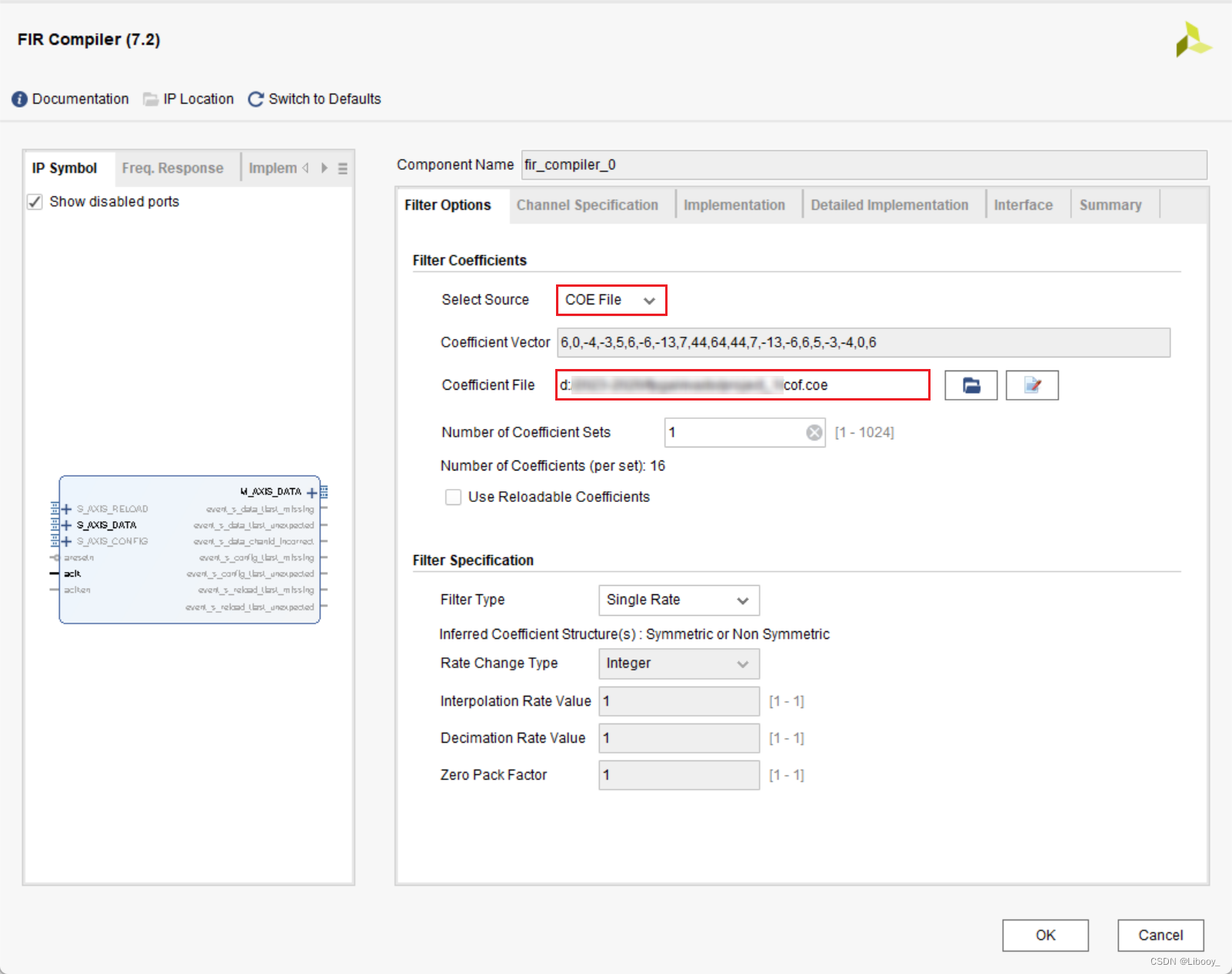
②在Filter Options中将Select Source设置为COE File，点击Cofficient File右侧的第一个框上传刚才MATLAB产生的.coe文件。

其他参数设置如下：

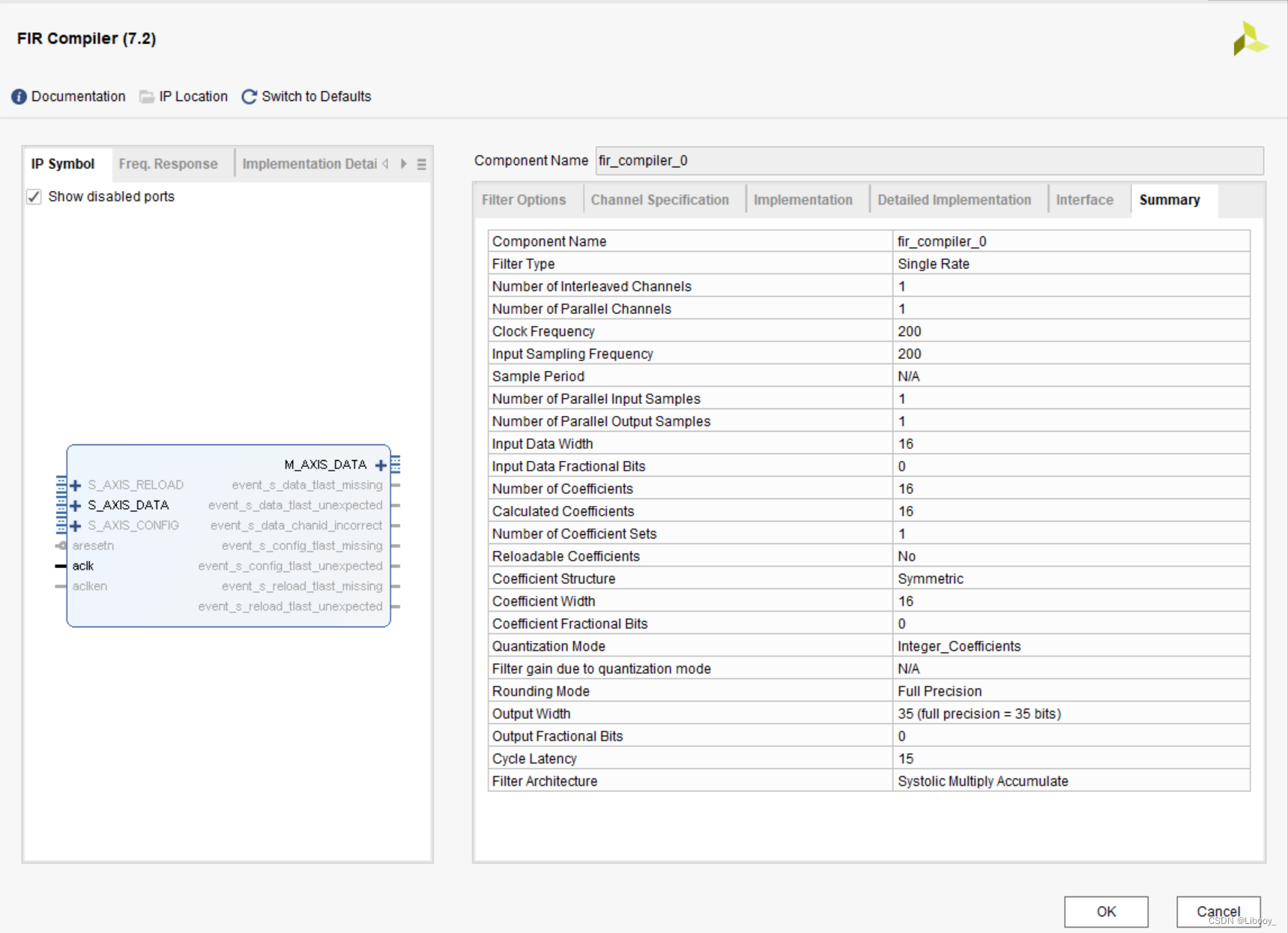
在MATLAB中设置的滤波器的采样频率为200MHz，在此要保持一致，即Input Sampling Frequency设置为200MHz。时钟频率Clock Frequency设置为200MHz，这里时钟频率和开发板保持一致即可，也应该和测试文件中的clk频率一致。输入数据位宽为16位，输出数据位宽为35位。

下图中输出数据为m_axis_data_tdata[39:0]，是40位，和Summary中Output Width不符。原因应该是这里设置成40位防止数据溢出，实际上是35位。

（2）代码

程序中认为输入的采样数据始终有效，因此将s_axis_data_tvalid永远置1。

`timescale 1ns / 1ps
module LowBandPassFilter(
    input clk,
    input [15:0] wave_in,
    output [39:0] wave_out,
    output m_tvalid,
    output s_tready
    );
fir_compiler_0 fir1 (
  .aclk(clk),                      
  .s_axis_data_tvalid(1'b1),       
  .s_axis_data_tdata(wave_in),    
  .s_axis_data_tready(s_tready),
  .m_axis_data_tvalid(m_tvalid),
  .m_axis_data_tdata(wave_out)   
);
endmodule

3.任务四：设计ROM

（1）MATLAB产生正弦波格式的COE文件

ROM的地址数为4096，数据位宽为16位，产生的信号幅值为10进制数。产生正弦信号表时，采用初始相位为0，周期为4096的波形，并且将正弦信号乘次方并乘（ 2 15 2^{15} 215-1）再加 2 15 2^{15} 215，将数据变换到[1, 2 16 2^{16} 216-1]范围内。回忆上文中提到，使用MATLAB产生滤波器进行滤波时，也要先加上直流分量，把信号搬移到正值，上文就是为了与此处保持一致。MATLAB中滤波器的输入要求为[-1,1]，信号搬移后，需要除以4满足滤波器的输入要求，所以在Vivado中，合路信号也需要右移2位（即除4），后文会提到这一点。

depth = 4096;   %存储器的单元数4096
widths = 16;    %数据宽度为16位
fidc = fopen('sine.coe','wt');  %给文件起名字
fprintf(fidc , 'memory_initialization_radix=%d;\nmemory_initialization_vector=\n',10);  
for x = 1 : depth-1
    fprintf(fidc,'%d,\n',round((2^(widths-1)-1)*sin(2*pi*(x-1)/4096)+2^(widths-1)));
end
fprintf(fidc,'%d;\n',round((2^(widths-1)-1)*sin(2*pi*(depth-1)/4096)+2^(widths-1)));
fclose(fidc);

产生的COE文件内容如下：

memory_initialization_radix=10;
memory_initialization_vector=
32768,
32818,
32869,
32919,
32969,
33019,
33070,
33120,
33170,
······//中间省略
32466,
32517,
32567,
32617,
32667,
32718;//最后为分号

（2）在Vivado中设置ROM IP核

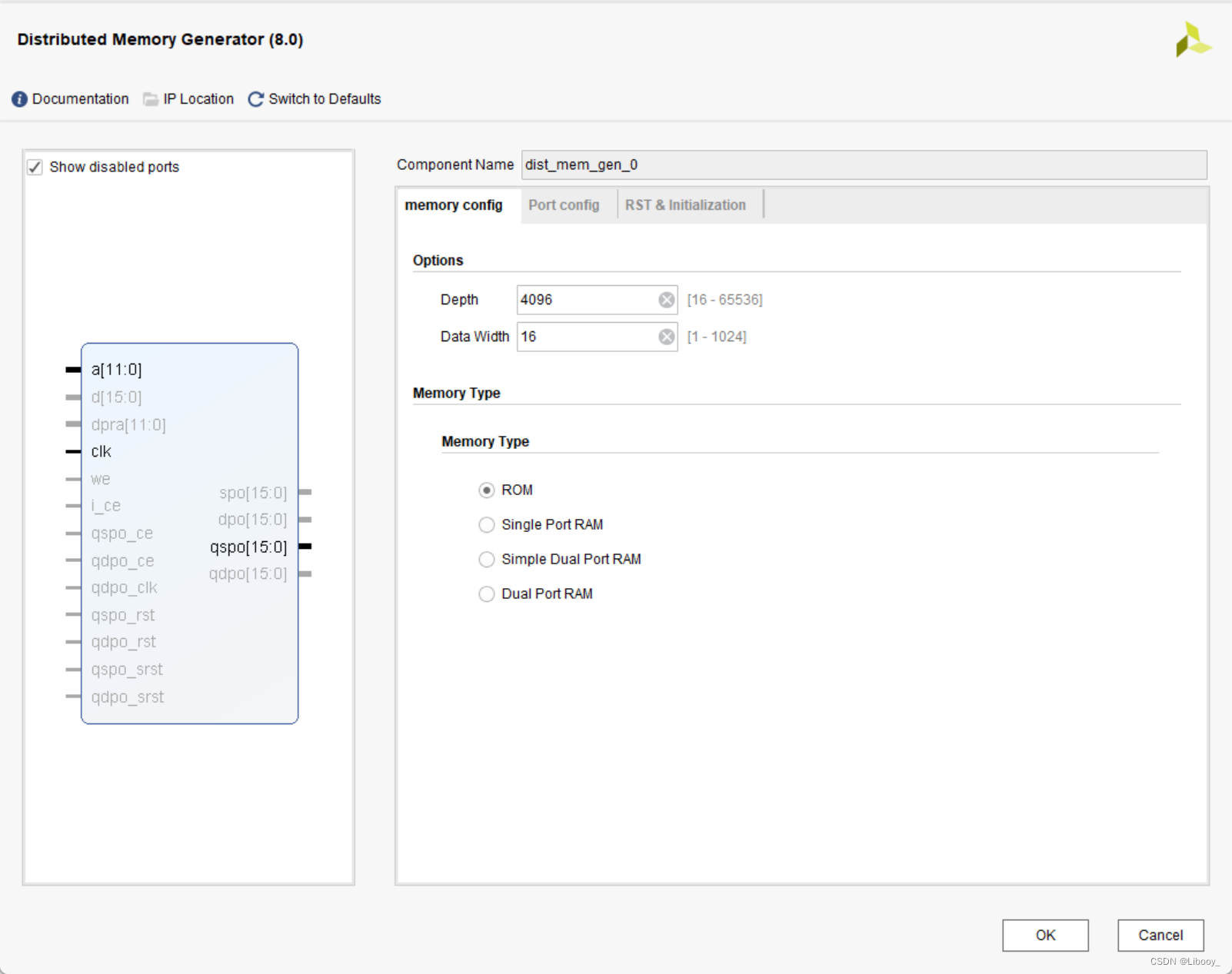
选择IP Catalog-Distributed Memory Generator

注：老师后来提醒我，Distributed Memory适合数据没那么多的时候，比如：16、32、64、128这样，1024、4096等数据规模较大的时候还是用Block Memory Generator比较好。

根据设计要求，ROM的深度为4096，数据位宽为16，即ROM的地址为12根，寻址范围0~4095，每一个地址上存储的数据为16位。

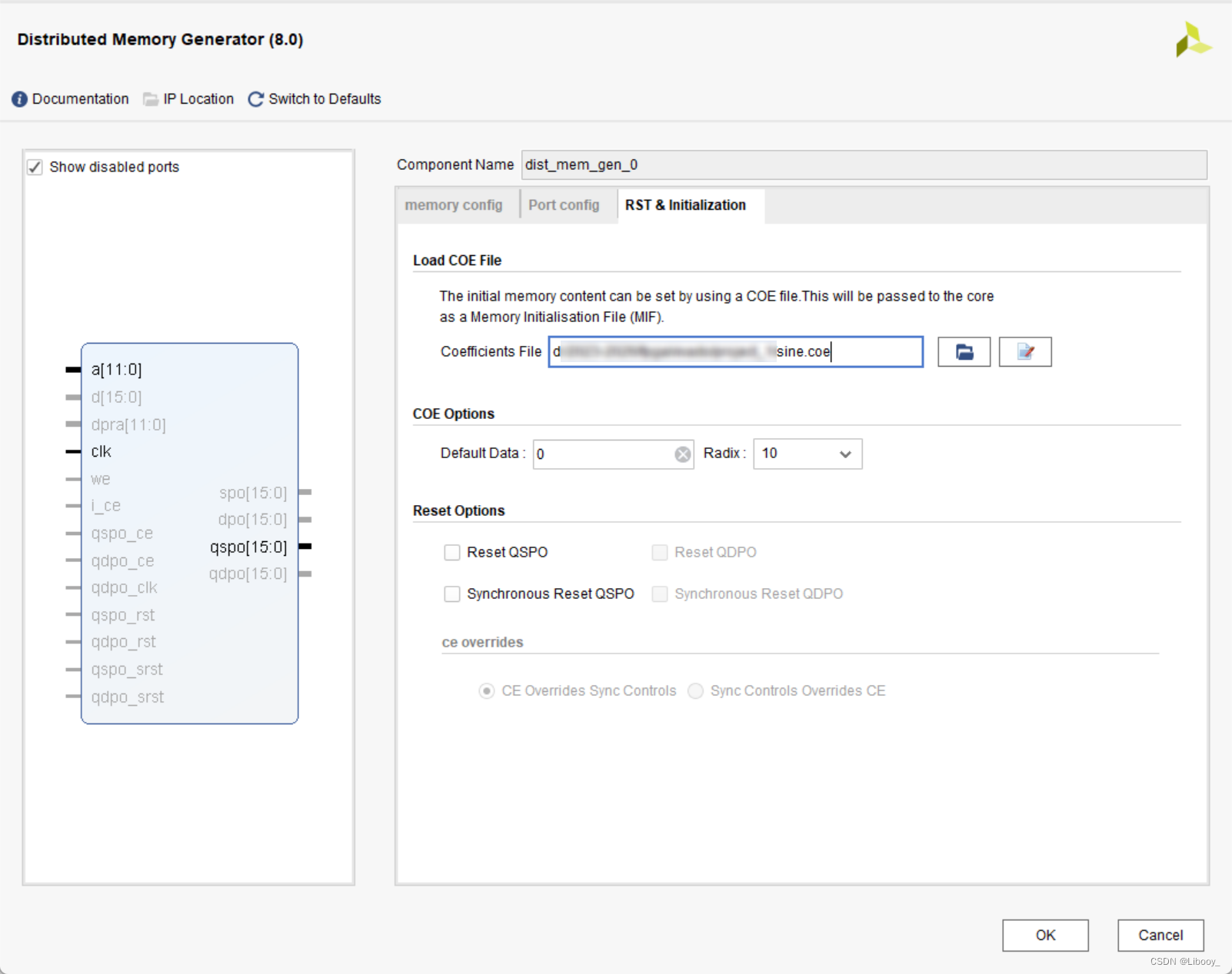
选择上一步中MATLAB生成的COE文件上传，Radix为10（与MATLAB生成时保持一致即可）。

（3）代码

`timescale 1ns / 1ps
module rom(                     
    input clk,                          //50M时钟
    //input rst,                          //复位
    output [15:0] data,                   //rom 输出的数据
    output [11:0] addr
);
 
dist_mem_gen_0 Rom (       
.a(addr), // input wire [11 : 0] a
.clk(clk), // input wire clk
.qspo(data) // output wire [15 : 0] qspo
);
endmodule

4.任务五：例化ROM产生不同频率的正弦信号

（1）思路

例化两个正弦信号ROM，通过控制地址的步进量的方式产生两个正弦信号输出，频率近似为3MHz和19MHz。即对ROM中的数据进行采样，采样频率不同，产生的信号频率也不同。其中，频率控制字的计算公式为： M = f o u t ∗ 2 N f c l k M=\frac{f_{out}*2^{N}}{f_{clk}} M=fclk​fout​∗2N​（1）。其中，N为位宽，M为频率控制字， f o u t {f_{out}} fout​为输出频率， f c l k {f_{clk}} fclk​ 为时钟频率200MHz。产生3MHz的信号时，根据公式（1）可知，频率控制字M为12’d61，同理产生19MHz信号的频率控制字为12’d389。

（2）产生3MHz正弦波代码

产生3MHz正弦波代码如下：

`timescale 1ns / 1ps
module DDS_3M(
    input clk,
    input reset,
    output [15:0] data_3M
    );
parameter fre_word = 12'd61;     //频率控制字     fre_word = f_out * 2^N / fclk   N为累加器位宽
reg [11:0] addr_sin;
//相位累加器
always @(posedge clk or reset)  
begin
    if(!reset)
        addr_sin >2;
assign wave_in = wave_inn[15:0];
initial begin
	clk = 1'b0;
    reset = 1'b0;
    #1 reset = 1'b1;
end
DDS wave(
    .clk(clk),
    .reset(reset),
    .data_3M(wave_3M),
    .data_19M(wave_19M)
);
LowBandPassFilter LBF(
     .clk(clk),
     .s_tready(s_tready),
     .wave_in(wave_in),
     .wave_out(m_tdata),
     .m_tvalid(m_tvalid)
);
endmodule

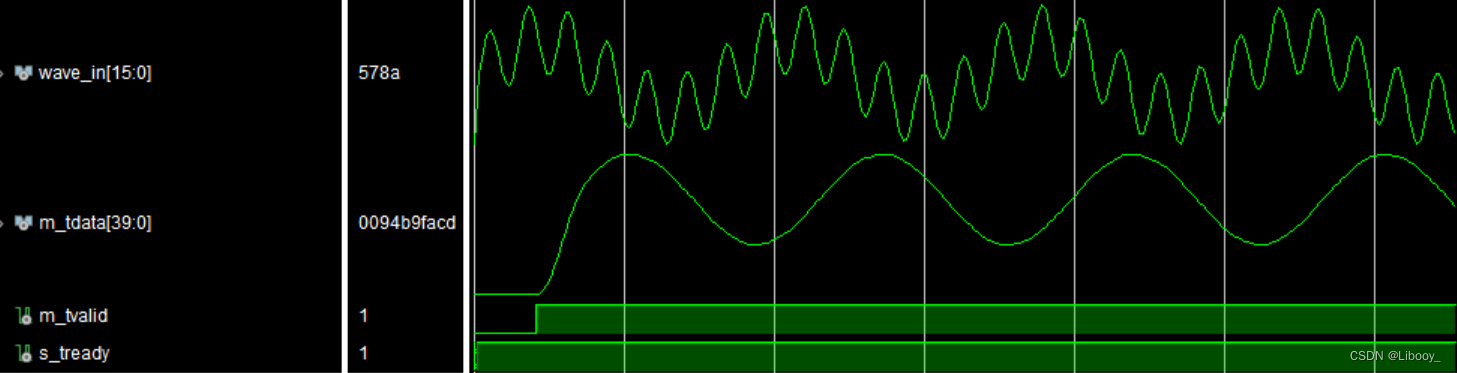
（2）结果分析

由下图可知，经过低通滤波器滤波后，输入的3M+19MHz信号（wave_in[15:0]）只剩下3MHz的单频信号。且当FIR滤波器输出有效时，m_tvalid信号置高。

三、结果分析

1.要求：

（1）误差分析

FFT的结果可以采用对数值分析，10log(x)（功率值）或20log(x) （幅度值），这样方便结合滤波器的滤波特性进行对比分析。

（2）时序分析

用250MHz、300MHZ、350MHZ和400MHz时钟进行分析，看设计的电路能够工作在哪个频率上。

（3）SNR分析

需要输入单音、多音冲击响应、多种随机信号进行分析。

2.误差分析

（1）思路

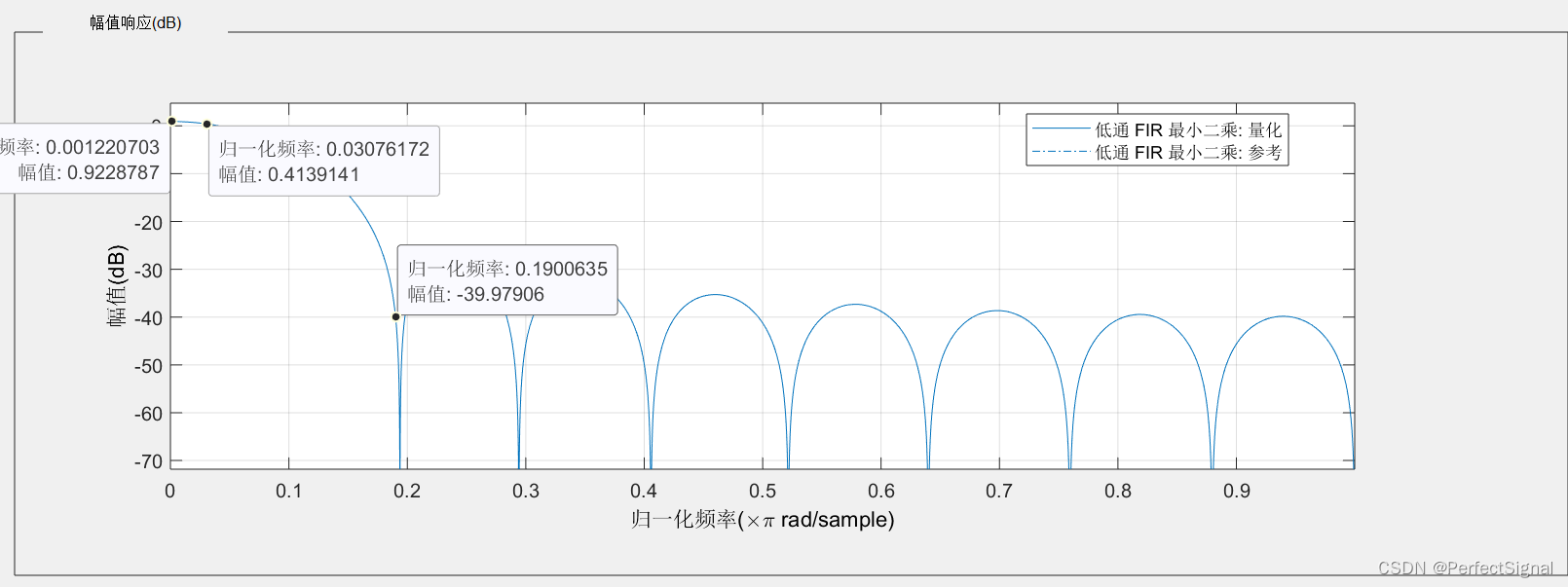
在Vivado中，两个频率的单音信号幅度都是一样的，合路信号经过滤波器后，两个频率的单音信号的幅度出现差异（我们期望的是3MHz的信号幅度没有衰减，而19MHz的信号幅度尽可能多地衰减），分析其真实差异值是否与MATLAB中滤波器的频率响应图上的两个频率的幅度差异一致。

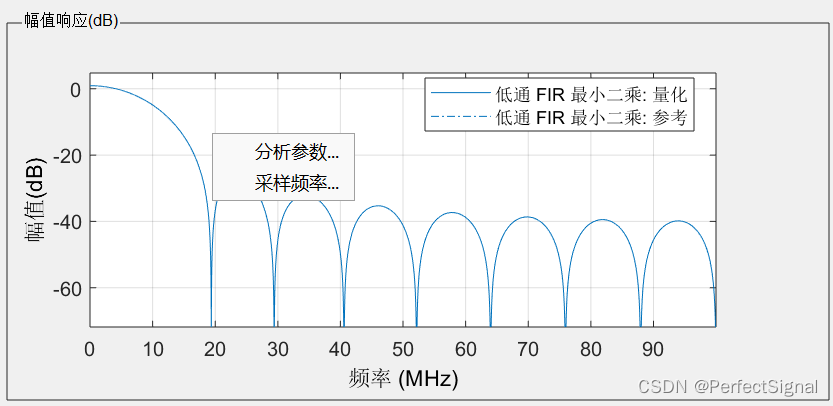
（2）在MATLAB中，查看并绘制FIR滤波器的幅值响应

①在APP-滤波器设计工具（ 或者在命令行窗口直接输入filterDesigner）打开任务一中设计的滤波器，即可以看到滤波器的幅值响应。

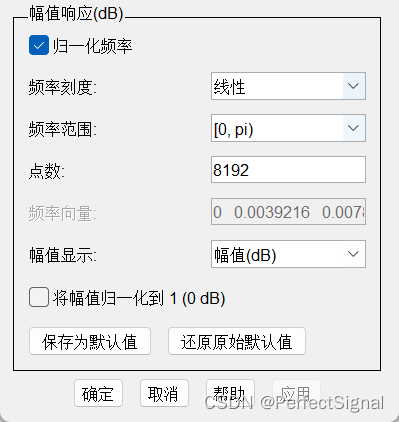
②在图上单击鼠标右键，可以选择分析参数和采样频率。

③在分析参数中，可以选择归一化频率（因为MATLAB中绘制的滤波器的幅值响应横坐标也是归一化频率，为方便对比在此统一）。

**频率归一化的定义：**滤波器中各个频率值以截止频率作归一化后，频率都是截止频率的相对值，没有了量纲。信号处理工具箱中经常使用的是奈奎斯特频率（也叫做分析频率、截止频率），它被定义为采样频率的二分之一，在滤波器的阶数选择和设计中的截止频率均使用奈奎斯特频率进行归一化处理。

实际物理频率表示AD采集物理信号的频率，fs为采样频率，由奈奎斯特采样定理可以知道，fs必须大于等于信号最高频率的2倍才不会发生信号混叠，因此fs能采样到的信号最高频率为fs/2。角频率是物理频率的2π倍，这个也称模拟频率。归一化频率是将实际物理频率除以分析频率，分析频率为采样频率的二分之一。

在本设计中，采样频率为200MHz，归一化频率即实际物理频率/分析频率，即际物理频率/100MHz。如果将归一化频率转换为角频率，则将归一化频率乘以2*pi。如果将归一化频率转换为Hz，则将归一化频率乘以分析频率。

④我们设计的滤波器的幅值响应如下图所示，可以单击图上的点建立游标数据，方便后续我们对比。

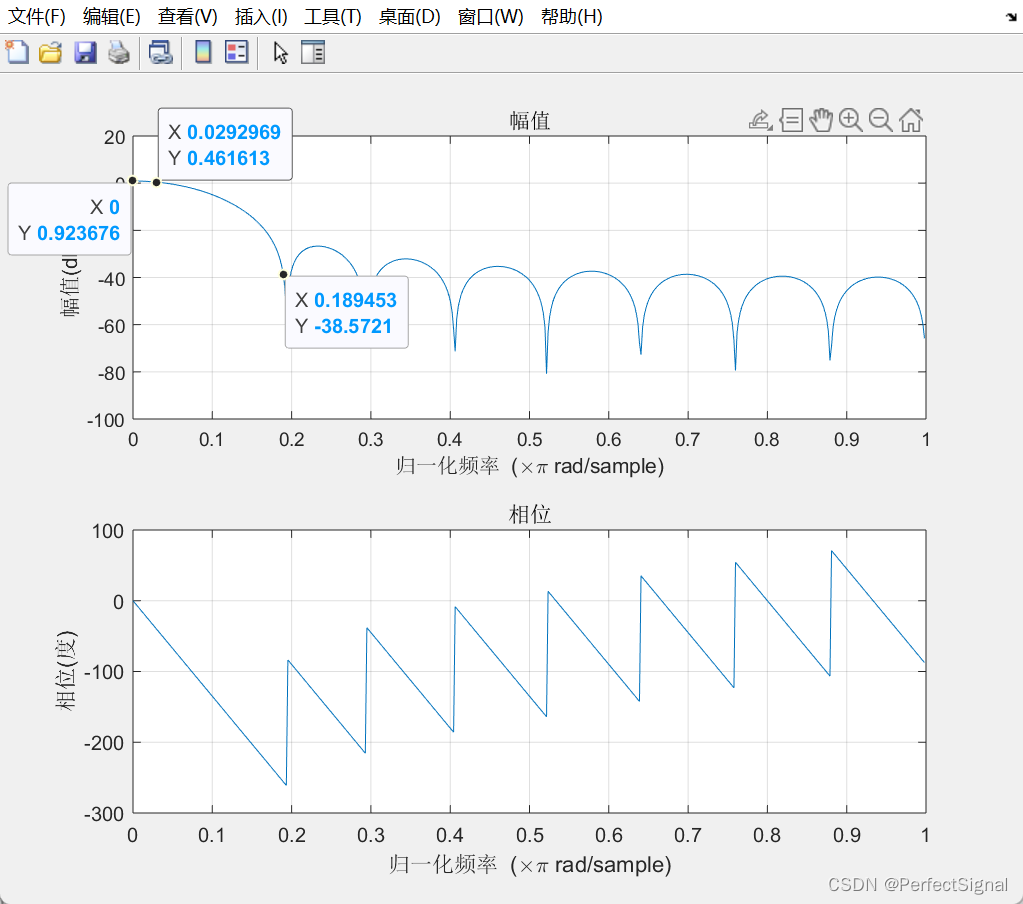
⑤通过代码绘制滤波器的幅值响应

添加的代码是：

%% 绘制滤波器的幅频响应
figure;
freqz(b);

更改后的低通滤波器的代码如下：

function Hd = lowpass_filter
% All frequency values are in MHz.
Fs = 200;  % Sampling Frequency
N     = 15;  % Order
Fpass = 8;   % Passband Frequency
Fstop = 15;  % Stopband Frequency
Wpass = 1;   % Passband Weight
Wstop = 1;   % Stopband Weight
% Calculate the coefficients using the FIRLS function.
b  = firls(N, [0 Fpass Fstop Fs/2]/(Fs/2), [1 1 0 0], [Wpass Wstop]);
Hd = dfilt.dffir(b);
%% 绘制滤波器的幅频响应
figure;
freqz(b);
% Set the arithmetic property.
set(Hd, 'Arithmetic', 'fixed', ...
    'CoeffWordLength', 16, ...
    'CoeffAutoScale', true, ...
    'Signed',         true, ...
    'InputWordLength', 16, ...
    'inputFracLength', 15, ...
    'FilterInternals',  'FullPrecision');
denormalize(Hd);

得到的幅值响应如下图所示：

（3）从Vivado中导入滤波前后信号的采样值

①在testbench文件中写入滤波后信号（m_tdata[39:0]）的值。

需要添加的代码如下：

reg [11:0] cnt;
integer file_sig_before_fir;
integer file_sig_after_fir;
always @(posedge clk) begin
    if(m_tvalid) begin
        if(cnt