【刷题】备战蓝桥杯 — dfs 算法
送给大家一句话:
风度真美!
即使流泪,也要鼓掌,
即使失望,也要满怀希望。
——刘宝增
dfs 算法
- 1 前言
- 2 洛谷 P1030 [NOIP2001 普及组] 求先序排列
- 题目描述
- 算法思路
- 3 洛谷 P1294 高手去散步
- 题目描述
- 算法思路
- 4 蓝桥真题 十三届省赛 飞机降落
- 题目描述
- 算法思路
- 5 总结
- Thanks♪(・ω・)ノ谢谢阅读!!!
- 下一篇文章见!!!
1 前言
在蓝桥杯的比赛中,深度优先搜索(DFS,Depth-First Search)算法是一种常用的搜索算法,它通过尽可能深地搜索树的分支,来寻找解决方案。由于其简单和易于实现的特性,DFS成为解决问题的强大工具,尤其是在数据规模较小的情况下。数据在100以内一般使用dfs
运行原理: DFS算法的核心思想是从一个起点开始,沿着树的边走到尽可能深的分支上,然后回溯到之前的分叉点,寻找未探索的分支。这个过程重复进行,直到找到解决方案或探索完所有可能的路径。DFS通常使用递归实现,这使得代码简洁易读。它利用栈(递归调用栈)来记录访问路径,从而实现回溯功能。基本蓝桥杯dfs算法题型可以使用以下模版:
#include //视情况而定 #define int long long #define endl '\n' #define N 1001 using namespace std; //往往需要一个哈希表来辅助判断 int vis[N] = {0}; void dfs() { //退出条件很重要!!! if() return ; for() { //跟新结果 //继续深入 dfs(); //回溯 } } signed main() { //加快读写速度 也可以直接使用C语言标准输入输出函数 ios::sync_with_stdio(0); cin.tie(0); cout.tie(0); //多组数据 int t = 0; cin >> t; while(t--) { //进行基础读入数据 //构建图 ,记录结构体等 //解决问题 dfs(); } return 0; }常用于以下题型:
- 路径问题: 寻找从起点到终点的路径,或者求解所有可能的路径。
- 排列组合问题: 需要枚举出所有可能的情况时,如全排列、组合选择。
- 连通性问题: 如判断图中两个节点是否连通,或者求解连通分量。
- 解谜与回溯问题: 如N 皇后问题、迷宫探索、数独解题等。
注意事项:
- 栈溢出问题(一般不用考虑): 由于DFS使用递归实现,深度过大时可能会导致栈溢出。针对这一点,可以尝试使用迭代深化搜索(IDS)或非递归方式实现DFS。
- 重复状态处理(一定要仔细): 在搜索过程中可能会遇到重复状态,如果不加以处理,可能会导致算法陷入无限循环。通常使用访问标记(如访问数组)来避免重复访问。
- 选择合适的剪枝策略(尽力而行): 合理的剪枝可以显著提高DFS的效率。通过预先判断某些路径是否可能达到目标,从而避免无效搜索。
通过以上的解析,我们可以看到DFS不仅在蓝桥杯中,在很多算法竞赛和实际问题解决中都是一个非常实用的工具。它虽然在处理大数据量时可能会遇到性能瓶颈,但在数据量适中、需要深度搜索解决方案的问题上,DFS仍然是一个十分可靠的选择。
下面我们来一起做几道竞赛题目来试试手!
2 洛谷 P1030 [NOIP2001 普及组] 求先序排列
题目描述
给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示,且二叉树的节点个数 ≤8)
输入格式
共两行,均为大写字母组成的字符串,表示一棵二叉树的中序与后序排列。
输出格式
共一行一个字符串,表示一棵二叉树的先序。
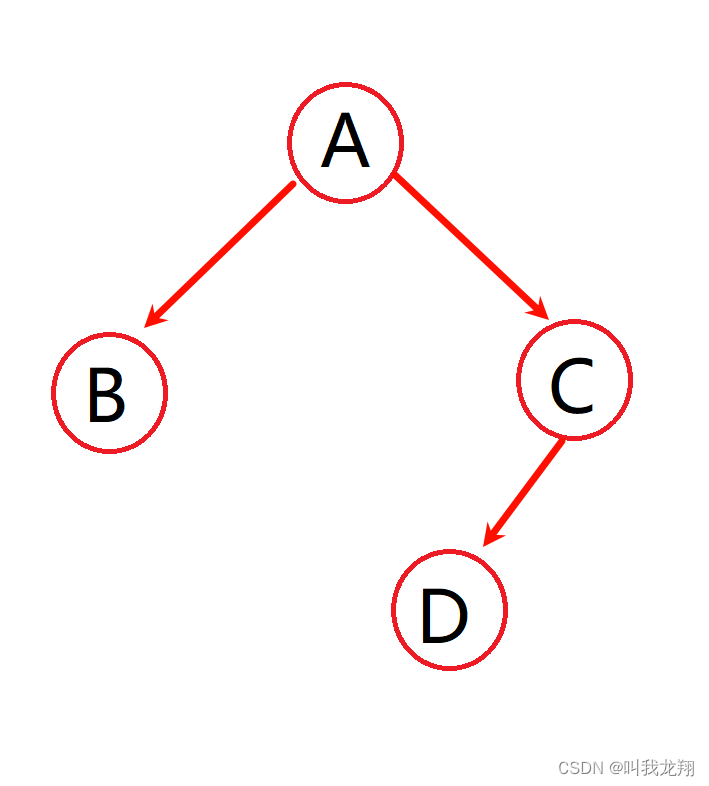
根据题目,我们需要通过二叉树的中序遍历和后序遍历来写出前序遍历的结果。对于二叉树的确定单凭中序遍历或者后序遍历是不可能的,只有两者结合才能确定一棵完整的二叉树!来看样例:
- 输入
BADC
BDCA
- 输出
ABCD
我们可以画出树的结构:
这样前序遍历的结果就有了
算法思路
这道题涉及了二叉树,那么如果不使用dfs 就会非常复杂捏!所以我们把解题交给dfs,重重递归解决问题:
- 首先通过后序遍历 , 我们可以确定根节点 (输出打印)
- 通过在中序遍历中找到根节点的位置,可以区分左右子树
- 区分出左右子树后,就可以继续寻找左右子树的根节点 ,重复1 - 2操作即可。
#include #include #define int long long using namespace std; void dfs(string in ,string af) { //为空时直接退出 if(in.size() //加快读写速度 也可以直接使用C语言标准输入输出函数 ios::sync_with_stdio(0); cin.tie(0); cout.tie(0); //通过string 来记录遍历的数据 比较方便(速度比较慢 数据量较小时问题不大) string in , af; cin in; cin >> af; //开始解决 dfs(in , af); }其中我们使用了string来记录遍历的数据 ,这样使用起来比较方便,但是速度比较慢(数据量较小时问题不大)。
然后通过不断寻找根节点,打印根节点来完成前序遍历。
提交!全部AC!!!
3 洛谷 P1294 高手去散步
链接:高手去散步
题目描述
鳌头山上有 n 个观景点,观景点两两之间有游步道共 m 条。高手的那个它,不喜欢太刺激的过程,因此那些没有路的观景点高手是不会选择去的。另外,她也不喜欢去同一个观景点一次以上。而高手想让他们在一起的路程最长(观景时它不会理高手),已知高手的穿梭机可以让他们在任意一个观景点出发,也在任意一个观景点结束。
输入格式
第一行,两个用空格隔开的整数 n 、 m 之后 m 行,为每条游步道的信息:两端观景点编号、长度。
输出格式
一个整数,表示他们最长相伴的路程。
根据题目描述,我们需要在一张地图中寻找最长的行走路线,直接使用暴力dfs是一种非常好的办法。
算法思路
这里需要对地图进行记录,相比直接的图标来记录(一个一个节点的地图)矩阵来记录地图更加方便,这里就是线性代数的美丽世界。通过 n x n的二维数据模拟矩阵,记录从一个节点前往另一个节点的距离,是不是非常方便:
1 2 3 4 1 0 0 0 0 2 0 0 0 0 3 0 0 0 0 4 0 0 0 0
这样的一张矩阵既可以记录4个景点之间是否有道路,并储存道路距离。
有了这张表,接下来的思路就简单了
- 首先先读入地图
- 让遍历所有的景点(因为出发点可以是任意一个),并进行最长路程计算
- 进行最长路程计算的过程是
- 通过选取地图找到还没有去过的景点,并更新距离,直到没有路为止
- 开始回溯,保证所以路线均被走过
#include #include #include using namespace std; //n 个景点 m 条路 int n , m; //用来判断是否去过 int hash1[20 + 20] = {0}; //地图矩阵 (+20 为了防止溢出) int map[20 + 20][20 + 20]; //答案 int maxpath = 0; void dfs(int i , int dis) { //对每一条路径进行搜索 for(int j = 1 ; j //存在道路 并且 没去过 进行搜索 if(map[i][j] && hash1[j] == 0) { //更新结果 hash1[j] = 1; //搜索 dfs(j , dis + map[i][j]); //回溯 这个很重要!!! hash1[j] = 0; } //不存在道路和没去过的景点 说明走完了 更新结果 取最大值 else{ maxpath = max(maxpath , dis); } } } signed main() { //加快读写速度 也可以直接使用C语言标准输入输出函数 ios::sync_with_stdio(0); cin.tie(0); cout.tie(0); //创建矩阵 cin > n >> m; while(m--) { //两个景点编号 间隔距离 int v1 ,v2 , dis; cin >> v1 >> v2 >> dis; //储存到地图中 map[v1][v2] = dis; map[v2][v1] = dis; } //对每个位置进行深度优先搜索 for(int i = 1 ; i int dis = 0; //记录来过 hash1[i] = 1; //怕什么 搜! dfs(i , dis) ; //回溯 这个很重要!!! hash1[i] = 0; //哈希表归零 memset(hash1 , 0 ,sizeof(hash1)); } cout 0}; struct plane { //T时刻到达 可以盘旋D时间 降落需要L时间 int T , D , L; }P[N]; bool flag = false; // 判断是否成功 void dfs(int n , int cnt , int time) { //已经降落的飞机数量等于总数,那么就成功 if(n == cnt) { flag = true; return ; } else { //遍历所有飞机 for(int i = 0 ; i t; while(t--) { int n = 0; cin >> n; int m = n; int i = 0; //读入飞机数据 while(m--) { cin >> P[i].T >> P[i].D >> P[i].L; i++; } //开始遍历 dfs(n , 0 , 0); if(flag) cout
- 输入