数据库:关系运算整理大全(包括关系代数、元组关系演算、域关系演算)
文章目录
- 关系运算
- 关系代数
- 基本关系代数运算
- 选择
- 投影
- 并
- 差
- 笛卡尔积
- 重命名
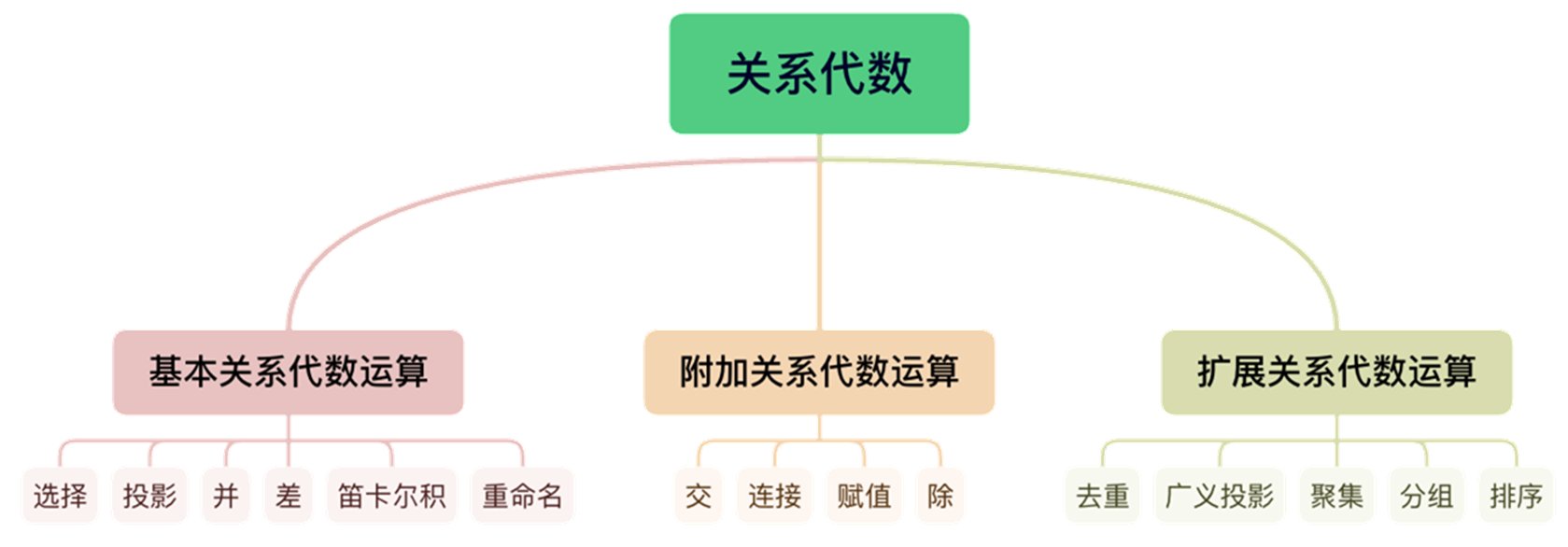
- 附加关系代数运算
- 交
- 连接
- 赋值
- 除
- 扩展关系代数运算
- 去重
- 广义投影
- 聚集
- 分组
- 排序
- ==总结==
- 元组关系演算
- 域关系演算
关系运算
- 关系运算包含
- 关系代数(relational algebra):关系代数是一种过程化查询语言,通过描述对关系的运算来表达查询、获取数据
- 关系演算:非过程化查询语言,通过描述想要获取的数据的信息来获取数据(不需要给出运算过程)
- 关系演算可以分为元组关系演算和域关系演算两种语言
- 为了方便用户查询处理关系数据,定义了结构化查询语言SQL 来操作处理关系数据
关系代数
- 关系代数定义了一个关系数据的运算的集合
- 关系运算以一个或者两个关系为输入;输出一个新的关系作为运算结果
- 关系是一个以元组为元素的多重集合(multiset):可能包含重复元素
- 关系代数运算本质上是对多重集合的运算
基本关系代数运算
包括选择、投影、并、差、笛卡尔积和重命名(期中,选择、投影、重命名为一元运算,并、差、笛卡尔积为二元运算)
基本关系代数运算可以用来表达任何传统关系代数运算
选择
选择运算 σ \sigma σ可以从关系 R R R中获取满足条件的元组:
σ p ( R ) = { t ∣ t ∈ R ∧ p ( t ) = True } \sigma_p(R)=\{t\mid t\in R\land p(t)=\text{True}\} σp(R)={t∣t∈R∧p(t)=True}
p p p为选择谓词:
- p p p是由逻辑运算符与 ∧ \land ∧、或 ∨ \lor ∨、非 ¬ \lnot ¬连接的若干原子表达式构成的公式
- 原子表达式的形式为:
X
□
Y
X\ \Box \ Y
X □ Y
- X , Y X,Y X,Y:属性名、常量,或者函数值
-
□
\Box
□为比较运算符,包括
=
>
\ t[A1,A2,…,Ak]∣t∈R}t∣t∈R∨t∈S}t∣t∈R∧t∈/S}t∣t∈R∧t∈S}ulliR和S中属性个数要相同/liliR和S中的属性应存在一一对应关系/liliR中每个属性的域和S中对应属性的域要相同
pmark交运算可以通过差运算来表示:
R
∩
S
=
R
−
(
R
−
S
)
R\cap S=R-(R-S)
R∩S=R−(R−S)/mark/p
h5连接/h5
p连接运算
⋈
\Join
⋈返回关系R和S笛卡尔积运算结果中满足一定条件的元组:/pp
R
⋈
p
S
=
{
(
t
,
q
)
∣
t
∈
R
∧
q
∈
S
∧
p
(
t
,
q
)
=
True
}
R\Join_{p}S=\{(t,q)\mid t\in R\land q\in S\land p(t,q)=\text{True}\}
R⋈pS={(t,q)∣t∈R∧q∈S∧p(t,q)=True}/p
p
p
p
p为选择谓词/p
ulli
p
p
p是由逻辑运算符与
∧
\land
∧、或
∨
\lor
∨、非
¬
\lnot
¬连接的若干原子表达式构成的公式/lili原子表达式的形式为:
R
.
X
Θ
S
.
Y
R.X\ \Theta\ S.Y
R.X Θ S.Y
ulliX是R的属性,Y是S的属性,X和Y所属域具有相同的数据类型/lili
Θ
\Theta
Θ:比较运算符,包括=、>、t∣t∈ΠA1,A2,…,An(R)∧(∀q∈S,(t,q)∈R)}t∣t∈R∧p(t)=True}t[A1,A2,…,Ak]∣t∈R}t∣t∈R∨t∈S}t∣t∈R∧t∈/S}t∣t∈R∧t∈S}t∣t∈ΠA1,A2,…,An(R)∧(∀q∈S,(t,q)∈R)}t∣P(t)}ulli上述表达式返回所有使得公式P为真的元组t的集合/liliP由原子公式组成,原子公式可以是以下形式之一:
olli
t
∈
R
t\in R
t∈R:其中t是元组变量,R是关系/lili
t
[
x
]
Θ
s
[
y
]
t[x]\Theta s[y]
t[x]Θs[y]:其中t和s是元组变量,x是t所属的关系的属性,y是s所属的关系的属性,
Θ
\Theta
Θ是比较运算符/lili
t
[
x
]
Θ
c
t[x]\Theta c
t[x]Θc,其中t,x,
Θ
\Theta
Θ同上,c是属性x的域中的常量/li/ol
pimg src="https://img-blog.csdnimg.cn/img_convert/5708567decb9256e9471b41524332f3e.png" //p
h3域关系演算/h3
ulli域关系演算也是非过程化查询语言/lili域关系演算使用属性域中取值的域变量来代替元组关系演算中的元组变量
p域关系演算表达式的定义为:
{
∣
P
(
x
1
,
x
2
,
…
,
x
k
)
}
\{\mid P(x_1,x_2,\dots,x_k)\}
{∣P(x1,x2,…,xk)}
- 其中 x 1 , x 2 , … , x k x_1,x_2,\dots,x_k x1,x2,…,xk均为域变量, P P P是由原子公式组成的公式
- 上述表达式返回所有使得公式 P P P为真的域变量 x 1 , x 2 , … , x k x_1,x_2,\dots,x_k x1,x2,…,xk组成的元组的集合
- 原子公式可以是以下形式之一:
- ∈ R \in R ∈R,其中R是包含k个属性的关系, x 1 , x 2 , … , x k x_1,x_2,\dots,x_k x1,x2,…,xk为域变量或域常量
- x Θ y x\ \Theta\ y x Θ y,其中x和y是域变量, Θ \Theta Θ是比较运算符(包括>,
- 关系运算包含