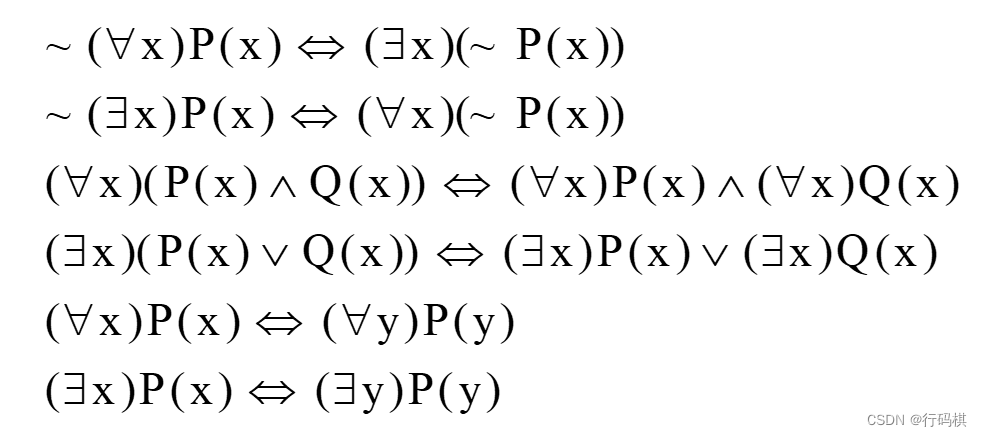人工智能及其应用（蔡自兴）期末复习

07-11 1489阅读

人工智能及其应用（蔡自兴）期末复习

本文是基于郑州大学人工智能课程制作的复习笔记，教学内容基本很陈旧，应该很久都不会更新。

⭐️ 都是我们的复习重点，需要进行关注

人工智能太恶心了，内容太多了！

注：我只是按照我们的课件来进行复习，不要盲目相信我的主观观点！！！每年教的老师是不一样的，课件也是不一样的！！！我们当年的老师是 tz、wzc

😋 更多复习科目请查看： 2020级郑州大学物联网工程期末记录 😋

原Markdown文件获取请跳转：https://github.com/anda522/CourseReview

相关资料：

人工智能期末复习

人工智能复习题

人工智能模拟卷

人工智能期末练习题

1 ⭐️绪论

人工智能：人工智能就是用人工的方法在机器（计算机）上实现的智能，或称机器智能、计算机智能。

人工智能发展的三个阶段：

计算
感知
认知
⭐️人工智能发展时期：
- 孕育期（ 1956年前）：亚里士多德，莱布尼茨，图灵，莫克，麦克洛奇和皮兹，维纳
- 形成期（ 1956－1970年）：1956年第一次人工智能研讨会（达特茅斯会议），
- 暗淡期（ 1966－1974年）：过高预言
- 知识应用期（ 1970－1988年）：专家系统的出现
- 集成发展期（ 1986年至今）：AI技术进一步研究
  
  ⭐️人工智能学派：
  - 符号主义（功能模拟方法）：逻辑主义，以物理符号系统为原理，代表：纽厄尔，肖，西蒙，尼尔逊
  - 连接主义（结构模拟方法）：仿生学派，神经网络之间连接机制为原理，代表：卡洛克，皮茨，霍普菲尔德，鲁梅尔哈特
  - 行为主义（行为模拟方法）：控制论学派，类似于控制机器人，代表：布鲁克斯
    人工智能应用：问题求解和博弈，逻辑推理和定理证明，计算智能，分布式人工智能和真体，自动程序设计，专家系统，机器学习，自然语言理解，机器人学，模式识别，机器视觉，神经网络，智能控制
    
    人工智能系统分类：专家系统，模糊系统，神经网络系统，学习系统，仿生系统，群智能系统，多真体系统，混合智能系统
    
    目标：
    - 近期目标：建造智能计算机代替人类的部分智力劳动
    - 远期目标：揭示人类智能的根本机理，用智能机器去模拟、延伸和扩展人类的智能
      研究的基本内容：认知建模，知识表示，知识推理，知识应用，机器感知，机器思维，机器学习，机器行为，智能系统构建
      
      2 知识表示
      
      2.1 ⭐️状态空间表示
      
      概念理解：状态，算符
      
      状态表示（知道初始状态和目标状态），状态表示图的画法
      
      相关问题：
      - 野人传教士渡河问题
        ( a , b , c ) (a, b, c) (a,b,c)表示（左岸传教士人数，左岸野人数，左岸船数）
        
        梵塔问题
        状态： ( S A , S B ) (S_A, S_B) (SA,SB)， S A S_A SA表示 A A A所在杆号， S B S_B SB表示 B B B所在杆号， S A , S B ∈ { 1 , 2 , 3 } S_A,S_B \in \{1, 2, 3\} SA,SB∈{1,2,3}，全部状态为：
        ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 2 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 3 , 1 ) , ( 3 , 2 ) , ( 3 , 3 ) (1,1), (1, 2), (1, 3), (2, 1), (2, 2),(2,3),(3,1),(3,2),(3,3) (1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)
        初始状态： ( 1 , 1 ) (1,1) (1,1)，目标状态： ( 3 , 3 ) (3,3) (3,3)
        
        状态空间图：
        
        八数码问题
        2.2 ⭐️归约表示（与或图）
        
        需要理解：归约表示思路，与或图表示
        
        梵塔问题（四阶为例）
        假设用向量 ( D 4 , D 3 , D 2 , D 1 ) (D_4, D_{3},D_2, D_1) (D4,D3,D2,D1)表示从大到小的圆盘所在的柱子号，则
        
        初始状态： ( 1 , 1 , 1 , 1 ) (1, 1, 1, 1) (1,1,1,1)
        
        目标状态： ( 3 , 3 , 3 , 3 ) (3, 3, 3, 3) (3,3,3,3)
        
        问题归约为子问题：
        
        移动3，2，1号圆盘至2号柱子
        移动4号圆盘至3号柱子
        移动3，2，1号圆盘至3号柱子
        归约图表示：
        
        2.3 谓词逻辑表示
        
        概念理解：谓词，项，谓词公式，原子公式，合式公式
        
        合式公式性质：
        
        自然语言转换成谓词：
        
        人都会死
        ( ∀ x ) ( m a n ( x ) → d i e ( x ) ) (\forall x) (man(x) \to die(x)) (∀x)(man(x)→die(x))
        
        有的人聪明
        ( ∃ x ) ( m a n ( x ) → c l e v e r ( x ) ) (\exist x) (man(x) \to clever(x)) (∃x)(man(x)→clever(x))
        
        谓词推理：
        
        下面的例子使用了 P ∨ Q ¬ P ∨ Q ⟹ Q ∨ Q = Q P \lor Q \hspace{1em} \neg P \lor Q \implies Q \lor Q = Q P∨Q¬P∨Q⟹Q∨Q=Q 消解推理规则
        
        
        2.4 语义网络表示
        
        常用语义联系：
        
        推理机制：匹配和继承
        
        2.5 框架表示
        
        结构：
        
        节点
        槽：每个槽可有多个侧面，每个侧面可有多个值
        值
        推理机制：
        
        匹配
        填槽（查询，默认，继承，附加过程计算）
        大学教师的框架：
        
        2.6 ⭐️知识表示方法的联系
        
        
        
        3 搜索推理
        
        3.1 ⭐️盲目搜索（无信息搜索）
        
        本小节没有加以整理，请看课件
        
        ⭐️深度优先搜素
        ⭐️宽（广）度优先搜索
        等代价搜索（UCS）：就是Dijkstra算法
        有界深搜：就是限制深度的深搜
        迭代加深算法（IDS）
        知道OPEN表和CLOSED表的作用
        
        3.2 ⭐️启发式搜索（有信息搜索）
        
        按选择范围不同分为：全局择优搜索（A,A*）和局部择优搜素
        f ( x ) = g ( x ) + h ( x ) f(x) = g(x) + h(x) f(x)=g(x)+h(x)
        h ( x ) h(x) h(x)：启发函数
        
        搜索算法：
        
        A算法： h ( x ) h(x) h(x)不做限制
        
        A*算法： h ( x ) h(x) h(x)有限制
        
        3.3 ⭐️消解原理（归结原理）
        
        就是对几个子句推导出新的子句（几个公理推导出新的结论）
        
        ⭐️如何求子句集（将谓词演算公式化成子句集）P97
        子句集特征：没有蕴涵词（ → \rightarrow →）、等值词（ ↔ , ≡ \leftrightarrow, \equiv ↔,≡）, ¬ \neg ¬作用原子谓词，没有全称和存在量词，合取范式，元素之间变元不同，集合形式
        
        
        
        ⭐️消解推理规则
        P ¬ P ∨ Q ⟹ Q P ∨ Q ¬ P ∨ Q ⟹ Q ∨ Q = Q ¬ P P ⟹ N I L ¬ P ∨ R ( P → R ) ¬ Q ∨ R ( Q → R ) ⟹ ¬ P ∨ Q ( P → Q ) P \hspace{1em} \neg P \lor Q \implies Q \\ P \lor Q \hspace{1em} \neg P \lor Q \implies Q \lor Q = Q \\ \neg P \hspace{1em} P \implies NIL \\ \neg P \lor R(P \to R) \hspace{1em} \neg Q \lor R(Q \to R) \implies \neg P \lor Q(P \to Q) P¬P∨Q⟹QP∨Q¬P∨Q⟹Q∨Q=Q¬PP⟹NIL¬P∨R(P→R)¬Q∨R(Q→R)⟹¬P∨Q(P→Q)
        
        消解反演
        消解通过反演来证明。将目标公式否定添加到命题公式集中，从中推导出一个空子句。（类似于反证法，否定结论，并将其作为条件，推导出一个空结论，即不可能满足的结论）
        
        反演树的画法与理解
        
        置换与合一的概念
        置换： σ = { f ( a ) / x , f ( y ) / z } \sigma = \{f(a) / x , f(y) / z\} σ={f(a)/x,f(y)/z} 代表用 f ( a ) f(a) f(a)代替掉 x x x，用 f ( y ) f(y) f(y)代替掉 z z z。
        
        合一：寻找一个置换，使两个表达式一致的过程。
        
        3.4 规则演绎
        
        产生式系统
        产生式规则一般形式：
        
        I F A 1 , A 2 , . . . , A n T H E N B IF \hspace{1em} A_1,A_2,...,A_n \hspace{1em} THEN \hspace{1em} B IFA1,A2,...,AnTHENB
        
        逻辑蕴含式是产生式的一种特殊形式。
        
        产生式系统的组成：
        
        总数据库
        产生式规则（规则库）
        控制策略（推理机）
        产生式系统的推理：正向推理，逆向推理，双向推理。
        
        3.5 不确定性推理
        
        三种不确定性程度：
        
        知识不确定性
        证据不确定性
        结论不确定性
        不确定性表示度量：
        
        静态强度：知识的不确定性程度表示，（LS,LN）为知识的不确定性表示。
        动态强度：证据的不确定性程度表示
        3.5.1 ⭐️概率推理
        
        条件概率公式：
        P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B) = \frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)
        
        全概率公式：（ A i A_i Ai构成一个完备事件组，互相独立，其总和为全集）
        P ( B ) = ∑ i = 1 n P ( A i ) P ( B ∣ A i ) P(B) = \sum \limits_{i = 1}^n P(A_i)P(B|A_i) P(B)=i=1∑nP(Ai)P(B∣Ai)
        
        贝叶斯公式：（先验概率 P ( H ) P(H) P(H)，条件概率 P ( H ∣ E ) P(H|E) P(H∣E)）
        P ( H ∣ E ) = P ( H ) P ( E ∣ H ) P ( E ) P ( B i ∣ A ) = P ( B i ) P ( A ∣ B i ) ∑ i P ( B i ) P ( A ∣ B i ) P ( H i ∣ E 1 E 2 ⋯ E m ) = P ( E 1 ∣ H i ) P ( E 2 ∣ H i ) ⋯ P ( E m ∣ H i ) P ( H i ) ∑ j = 1 n P ( E 1 ∣ H j ) P ( E 2 ∣ H j ) ⋯ P ( E m ∣ H j ) P ( H j ) P(H|E) = \frac{P(H)P(E|H)}{P(E)} \\ P(B_i | A) = \frac{P(B_i)P(A|B_i)}{\sum_i P(B_i) P(A|B_i)} \\ P(H_i | E_1E_2 \cdots E_m) = \frac{P(E_1|H_i)P(E_2|H_i) \cdots P(E_m|H_i)P(H_i)}{\sum \limits_{j = 1}^n P(E_1|H_j)P(E_2|H_j) \cdots P(E_m|H_j)P(H_j)} P(H∣E)=P(E)P(H)P(E∣H)P(Bi∣A)=∑iP(Bi)P(A∣Bi)P(Bi)P(A∣Bi)P(Hi∣E1E2⋯Em)=j=1∑nP(E1∣Hj)P(E2∣Hj)⋯P(Em∣Hj)P(Hj)P(E1∣Hi)P(E2∣Hi)⋯P(Em∣Hi)P(Hi)
        
        3.5.2 ⭐️ 主观贝叶斯（？我们是没有考，但是你们就不一定了）
        
        相关公式：
        O ( X ) = P ( X ) 1 − P ( X ) O ( H ∣ E ) = L S ⋅ O ( H ) O ( H ∣ ¬ E ) = L N ⋅ O ( H ) O ( H ∣ S 1 , S 2 , ⋯ , S n ) = O ( H ∣ S 1 ) O ( H ) ⋅ O ( H ∣ S 2 ) O ( H ) ⋯ O ( H ∣ S n ) O ( H ) ⋅ O ( H ) O(X) = \frac{P(X)}{1 - P(X)} \\ O(H|E) = LS \cdot O(H) \\ O(H| \neg E) = LN \cdot O(H) \\ O(H|S_1, S_2, \cdots, S_n) = \frac{O(H|S_1)}{O(H)} \cdot \frac{O(H|S_2)}{O(H)} \cdots \frac{O(H|S_n)}{O(H)} \cdot O(H) O(X)=1−P(X)P(X)O(H∣E)=LS⋅O(H)O(H∣¬E)=LN⋅O(H)O(H∣S1,S2,⋯,Sn)=O(H)O(H∣S1)⋅O(H)O(H∣S2)⋯O(H)O(H∣Sn)⋅O(H)
        
        EH公式：
        P ( H ∣ S ) = { P ( H ∣ ¬ E ) + P ( H ) − P ( H ∣ ¬ E ) P ( E ) × P ( E ∣ S ) 0 ≤ P ( E ∣ S ) 0(2)
        
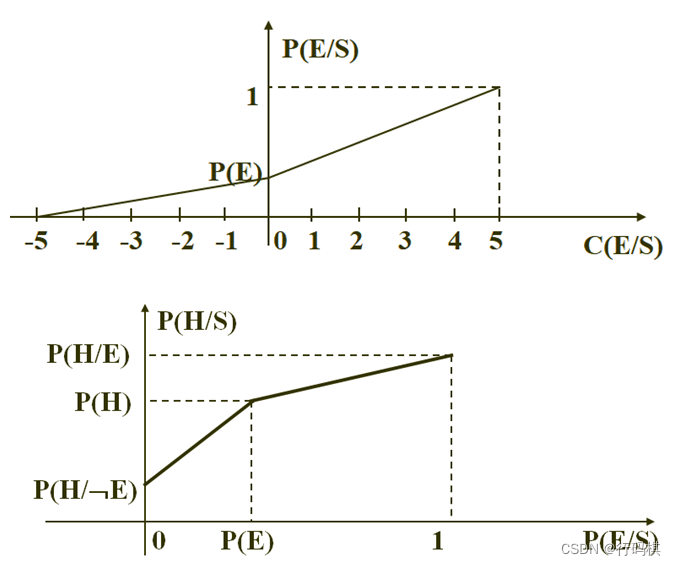
        根据第一张图得到 P ( E ∣ S ) P(E|S) P(E∣S)与 C ( E ∣ S ) C(E|S) C(E∣S)的关系，记为式 ( 3 ) (3) (3)
        
        根据第二张图得到 P ( H ∣ S ) P(H|S) P(H∣S)与 P ( E ∣ S ) P(E|S) P(E∣S)的关系，即为式 ( 1 ) (1) (1)
        
        将式 ( 3 ) (3) (3)代入到式 ( 1 ) (1) (1)中，得到CP公式
        
        
        
        3.5.3 ⭐️可信度方法
        
        可信度表示知识或证据的不确定性，范围 [ − 1 , 1 ] [-1,1] [−1,1]
        
        知识的不确定性表示：
        
        if E then H (CF(H, E))
        
        CF(H,E)：是该条知识的可信度，称为可信度因子或规则强度，它指出当前提条件 E 所对应的证据为真时，它对结论为真的支持程度。
        
        推理结论CF值计算：
        C F ( H ) = C F ( H , E ) × m a x { 0 , C F ( E ) } CF(H) = CF(H, E) \times max\{0, CF(E) \} CF(H)=CF(H,E)×max{0,CF(E)}
        重复结论CF值计算：
        i f E 1 t h e n H ( C F ( H , E 1 ) ) i f E 2 t h e n H ( C F ( H , E 2 ) ) 则 C F 1 , 2 ( H ) = { C F 1 ( H ) + C F 2 ( H ) − C F 1 ( H ) × C F 2 ( H ) C F 1 ( H ) ≥ 0 , C F 2 ( H ) ≥ 0 C F 1 ( H ) + C F 2 ( H ) + C F 1 ( H ) × C F 2 ( H ) C F 1 ( H )

VPS购买请点击我

文章版权声明：除非注明，否则均为主机测评原创文章，转载或复制请以超链接形式并注明出处。

相关阅读

目录[+]