【PCL】—— 点云配准ICP(Iterative Closest Point)算法

07-11 1280阅读

文章目录

数学原理
- 问题定义
- 计算平移
- 计算旋转
- 案例实现
- 参考
  由于三维扫描仪设备受到测量方式和被测物体形状的条件限制，一次扫描往往只能获取到局部的点云信息，进而需要进行多次扫描，然后每次扫描时得到的点云都有独立的坐标系，不可以直接进行拼接。在逆向工程、计算机视觉、文物数字化等领域中，由于点云的不完整、旋转错位、平移错位等，使得要得到完整点云就需要对多个局部点云进行配准。为了得到被测物体的完整数据模型,需要确定一个合适的坐标变换，将从各个视角得到的点集合并到一个统一的坐标系下形成一个完整的数据点云，然后就可以方便地进行可视化等操作，这就是点云数据的配准。
  
  点云配准步骤上可以分为粗配准（Coarse Registration）和精配准（Fine Registration）两个阶段。
  
  粗配准是指在点云相对位姿完全未知的情况下对点云进行配准，找到一个可以让两块点云相对近似的旋转平移变换矩阵，进而将待配准点云数据转换到统一的坐标系内，可以为精配准提供良好的初始值。
  
  精配准是指在粗配准的基础上，让点云之间的空间位置差异最小化，得到一个更加精准的旋转平移变换矩阵。该算法的运行速度以及向全局最优化的收敛性却在很大程度上依赖于给定的初始变换估计以及在迭代过程中对应关系的确立。所以需要各种粗配准技术为ICP算法提供较好的位置，在迭代过程中确立正确对应点集能避免迭代陷入局部极值，决定了算法的收敛速度和最终的配准精度。
  
  比较常见的一种配准算法是迭代最近点算法(Iterative Closest Point, ICP)。ICP算法可以基于四元数求解，也可以基于奇异值分解（SVD）求解，本文主要介绍基于奇异值分解的ICP算法。
  
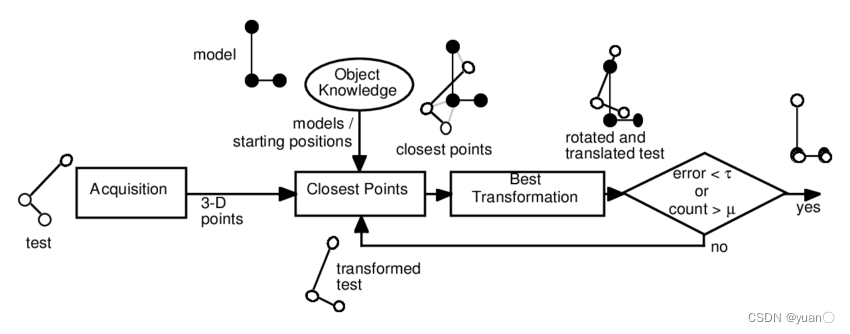
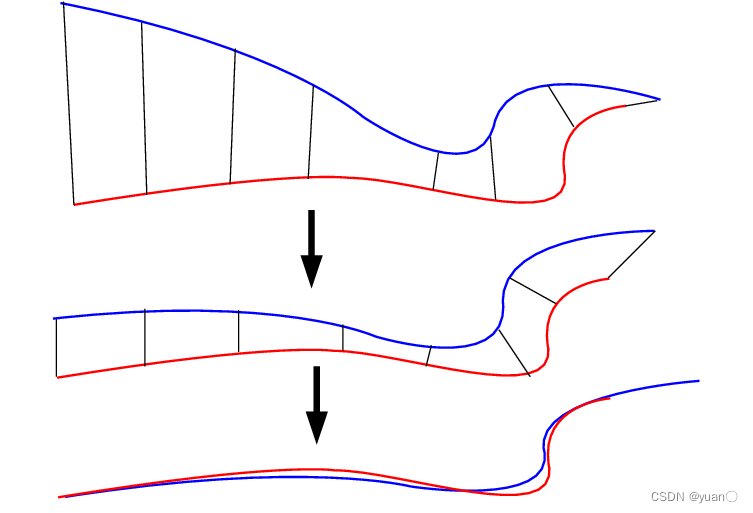
  ICP算法原理：给定一个参考点集 P P P和一个数据点集 Q Q Q（在给定的初始估计 R R R， t t t），算法为 Q Q Q中的每个点寻找 P P P中对应的最近点，形成匹配点对。然后，将所有匹配点对的欧氏距离之和作为待求解的目标函数，利用奇异值分解求出 R R R和 t t t以使目标函数最小，根据 R R R, t t t转换得到新的 Q ′ Q' Q′，并再次找到对应的点对，如此迭代。
  缺点：需要剔除噪声点（距离过大的点对或包含边界点的点对）。基于点对的配准不包括局部形状信息。在每次迭代中搜索最近点非常耗时。计算可能陷入局部最优。
  
  一般来说，ICP可以分为以下四个阶段
  1. 对原始点云数据进行采样
  2. 确定初始对应点集
  3. 去除错误对应点集
  4. 坐标变换的求解
  数学原理
  
  问题定义
  
  本部分结合了网上的一些资料以及自己的一些理解，可能不一定正确，部分步骤有所省略，具体可参考文末参考文献。
  
  定义两个点云集合 P = { p 1 , p 2 , . . . , p n } P={\{p_1,p_2,...,p_n\}} P={p1,p2,...,pn}, Q = { q 1 , q 2 , . . . , q n } Q={\{q_1,q_2,...,q_n\}} Q={q1,q2,...,qn}，其中 P P P为参考点云集合， Q Q Q为数据点云集合。点云的配准即是需要将 Q Q Q通过一系列的旋转与平移得到目标 P P P，实际上两个点云集合不会完全相同，所以往往无法得到准确的 R R R和 t t t使二者完全重合，但可以使变换后的点云 Q Q Q尽可能靠近 P P P，因此可以将问题描述为:
  E ( R , t ) = arg min ⁡ R ∈ S O ( d ) , t ∈ R d ∑ i = 1 n w i ∥ R q i + t − p i ∥ 2 E( R,t) = {\argmin\limits_{R \in SO(d),t\in {\Reals^d}}}\sum\limits_{i = 1}^n {{w_i}{{\left\| {R{q_i} + t - {p_i}} \right\|}^2}} E(R,t)=R∈SO(d),t∈Rdargmini=1∑nwi∥Rqi+t−pi∥2
  
  即构建最小二乘问题，将之转化为目标函数的优化问题，求以使以下目标函数误差的平方和达到极小时的 R R R和 t t t。其中 w i w_i wi代表每个点的权重。 R R R 和 t t t是我们所要求的旋转矩阵和平移向量。其中， d d d 表示 x x x 和 y y y的维度，通常情况下对于三维点云就是 d d d = 3，对于二维点云就是 d d d = 2。
  
  计算平移
  
  假设 R R R是常量，则先求平移向量 t t t ，令 ∂ E ∂ t = 0 \frac{{\partial E}}{{\partial t}} = 0 ∂t∂E=0 , 可得目标函数 ∂ E ∂ t = ∑ i = 1 n 2 w i ( R q i + t − p i ) = 2 t ( ∑ i = 1 n w i ) + 2 R ( ∑ i = 1 n w i q i ) − 2 ( ∑ i = 1 n w i p i ) = 0 \begin{array}{c}\frac{{\partial E}}{{\partial t}} = \sum\limits_{i = 1}^n {2{w_i}(R{q_i} + t - {p_i})} \\ = 2t\left( {\sum\limits_{i = 1}^n {{w_i}} } \right) + 2R\left( {\sum\limits_{i = 1}^n {{w_i}} {q_i}} \right) - 2\left( {\sum\limits_{i = 1}^n {{w_i}{p_i}} } \right) = 0\end{array} ∂t∂E=i=1∑n2wi(Rqi+t−pi)=2t(i=1∑nwi)+2R(i=1∑nwiqi)−2(i=1∑nwipi)=0
  
  令 p p p 的质心 μ p = 1 n ⋅ ∑ i = 1 n p i {\mu _p} = \frac{1}{n} \cdot \sum\limits_{i = 1}^n {{p_i}} μp=n1⋅i=1∑npi, q q q 的质心 μ q = 1 n ⋅ ∑ i = 1 n q i {\mu _q} = \frac{1}{n} \cdot \sum\limits_{i = 1}^n {{q_i}} μq=n1⋅i=1∑nqi.则可得 μ p − R μ q = t {\mu _p} - R{\mu _q} = t μp−Rμq=t
  
  将以上关系替换回原函数
  E ( R , t ) = arg min ⁡ R ∈ S O ( d ) , t ∈ R d ∑ i = 1 n w i ∥ R q i + t − p i ∥ 2 = arg min ⁡ R ∈ S O ( d ) , t ∈ R d ∑ i = 1 n w i ∥ R q i + μ p − R μ q − p i ∥ 2 = arg min ⁡ R ∈ S O ( d ) , t ∈ R d ∑ i = 1 n w i ∥ R ( q i − μ q ) + μ p − p i ∥ 2 = arg min ⁡ R ∈ S O ( d ) , t ∈ R d ∑ i = 1 n w i ∥ p ′ i − R q ′ i ∥ 2 \begin{array}{c}E(R,t) = {\argmin\limits_{R \in SO(d),t\in {\Reals^d}}} \sum\limits_{i = 1}^n {{w_i}{{\left\| {R{q_i} + t - {p_i}} \right\|}^2}} \\ = {\argmin\limits_{R \in SO(d),t\in {\Reals^d}}} \sum\limits_{i = 1}^n {{w_i}{{\left\| {R{q_i} + {\mu _p} - R{\mu _q} - {p_i}} \right\|}^2}} \\ = {\argmin\limits_{R \in SO(d),t\in {\Reals^d}}}\sum\limits_{i = 1}^n {{w_i}{{\left\| {R({q_i} - {\mu _q}) + {\mu _p} - {p_i}} \right\|}^2}} \\ = {\argmin\limits_{R \in SO(d),t\in {\Reals^d}}} \sum\limits_{i = 1}^n {{w_i}{{\left\| {{{p'}_i} - R{{q'}_i}} \right\|}^2}} \end{array} E(R,t)=R∈SO(d),t∈Rdargmini=1∑nwi∥Rqi+t−pi∥2=R∈SO(d),t∈Rdargmini=1∑nwi∥Rqi+μp−Rμq−pi∥2=R∈SO(d),t∈Rdargmini=1∑nwi∥R(qi−μq)+μp−pi∥2=R∈SO(d),t∈Rdargmini=1∑nwi∥p′i−Rq′i∥2
  这里， p i ′ , q i ′ p^′_i,q^′_i pi′,qi′ 分别是每个点云根据其质心坐标 μ p , μ q μ_p,μ_q μp,μq计算得到的去质心坐标：
  q ′ i = q i − μ q , p ′ i = p i − μ p {{q'}_i} = {q_i} - {\mu _q},{{p'}_i} = {p_i} - {\mu _p} q′i=qi−μq,p′i=pi−μp
  
  即求使得以下目标函数最小时， R R R的值
  E ( R , t ) = arg min ⁡ R ∈ S O ( d ) ∑ i = 1 n w i ∥ p ′ i − R q ′ i ∥ 2 E(R,t) = {\argmin\limits_{R \in SO(d)}} \sum\limits_{i = 1}^n {{w_i}{{\left\| {{{p'}_i} - R{{q'}_i}} \right\|}^2}} E(R,t)=R∈SO(d)argmini=1∑nwi∥p′i−Rq′i∥2
  
  计算旋转
  
  将 ∑ i = 1 n ∥ p ′ i − R q ′ i ∥ 2 \sum\limits_{i = 1}^n {{{\left\| {{{p'}_i} - R{{q'}_i}} \right\|}^2}} i=1∑n∥p′i−Rq′i∥2展开即可得到 ∑ i = 1 n p i ′ T p i ′ − 2 p i ′ T R q i ′ + q i ′ T R T R q i ′ \sum\limits_{i = 1}^n{p'_i}^T{p'_i} - 2{p'_i}^TR{q'_i} + {q'_i}^T{R^T}R{q'_i} i=1∑npi′Tpi′−2pi′TRqi′+qi′TRTRqi′
  此时，我们发现，除了第二项以外，目标函数其他部分都与参数R无关，进而在求解极值时可忽略。进而我们将问题转换为求解使以下目标函数最小时， R R R的值： E ( R , t ) = arg min ⁡ R ∈ S O ( d ) ∑ i = 1 n w i ⋅ ( − 2 ) p ′ i T R q ′ i E(R,t) = {\argmin\limits_{R \in SO(d)}} \sum\limits_{i = 1}^n {{w_i} \cdot \left( { - 2} \right){{p'}_i}^TR{{q'}_i}} E(R,t)=R∈SO(d)argmini=1∑nwi⋅(−2)p′iTRq′i = arg max ⁡ R ∈ S O ( d ) ∑ i = 1 n w i p ′ i T R q ′ i = {\argmax \limits_{R \in SO(d)}} \sum\limits_{i = 1}^n {{w_i}{{p'}_i}^TR{{q'}_i}} =R∈SO(d)argmaxi=1∑nwip′iTRq′i
  
  根据矩阵迹的性质，我们有以下结论： ∑ i = 1 n w i p ′ i T R q ′ i = t r ( W P T R Q ) \sum\limits_{i = 1}^n {{w_i}{{p'}_i}^TR{{q'}_i}} = tr(W{P^T}RQ) i=1∑nwip′iTRq′i=tr(WPTRQ)因为 t r ( A B ) = t r ( B A ) tr(AB) = tr(BA) tr(AB)=tr(BA)所以 t r ( W P T R Q ) = t r ( ( W P T ) R Q ) = t r ( R Q W P T ) tr(W{P^T}RQ) = tr((W{P^T})RQ) = tr(RQW{P^T}) tr(WPTRQ)=tr((WPT)RQ)=tr(RQWPT)定义“协方差”矩阵 S = Q W P T S = QW{P^T} S=QWPT对 S S S 进行 SVD 分解： S = U Σ V T S = U\Sigma {V^T} S=UΣVT S S S为3x3矩阵， Σ \Sigma Σ为奇异值组成的对角矩阵， U , V T U,V^T U,VT为正交矩阵。
  
  **定理：**对于任意一个正定矩阵 A A T AA^T AAT和正交矩阵 B B B,都有 t r ( A A T ) ≥ t r ( B A A T ) tr(AA^T)\ge tr(BAA^T) tr(AAT)≥tr(BAAT)
  
  依据迹的性质，则可以得到旋转矩阵 R R R
  当 d e t ( V U T ) = 1 det(VU^T)=1 det(VUT)=1时， V U T VU^T VUT为所求旋转矩阵
  当 d e t ( V U T ) = − 1 det(VU^T)=-1 det(VUT)=−1时， V U T VU^T VUT为反射矩阵，可以通过以下方式计算 R = V [ 1 1 ⋱ ⋱ det ⁡ ( V U T ) ] U T R = V\left[ {\begin{array}{ccccccccccccccc}1&{}&{}&{}&{}\\{}&1&{}&{}&{}\\{}&{}& \ddots &{}&{}\\{}&{}&{}& \ddots &{}\\{}&{}&{}&{}&{\det (V{U^T})}\end{array}} \right]{U^T} R=V 11⋱⋱det(VUT) UT
  
  案例实现
  
  官方教程——https://pcl.readthedocs.io/projects/tutorials/en/master/iterative_closest_point.html#iterative-closest-point
```
#include 
#include 
#include 
#include 
int
main(int argc, char **argv) {
    // 定义输入和输出点云
    pcl::PointCloud::Ptr cloud_in(new pcl::PointCloud);
    pcl::PointCloud::Ptr cloud_out(new pcl::PointCloud);
    // 随机填充无序点云
    cloud_in->width = 5;
    cloud_in->height = 1;
    cloud_in->is_dense = false;
    cloud_in->points.resize(cloud_in->width * cloud_in->height);
    for (size_t i = 0; i points.size(); ++i) {
        cloud_in->points[i].x = 1024 * rand() / (RAND_MAX + 1.0f);
        cloud_in->points[i].y = 1024 * rand() / (RAND_MAX + 1.0f);
        cloud_in->points[i].z = 1024 * rand() / (RAND_MAX + 1.0f);
    }
    std::cout 
    printf ("Rotation matrix :\n");
    printf ("    | %6.3f %6.3f %6.3f | \n", matrix (0, 0), matrix (0, 1), matrix (0, 2));
    printf ("R = | %6.3f %6.3f %6.3f | \n", matrix (1, 0), matrix (1, 1), matrix (1, 2));
    printf ("    | %6.3f %6.3f %6.3f | \n", matrix (2, 0), matrix (2, 1), matrix (2, 2));
    printf ("Translation vector :\n");
    printf ("t = 
```