C语言-回溯法-地图着色问题
1.问题描述
1.1设计内容
已知中国地图,对各省进行着色,要求相邻省所使用的颜色不同,并保证使用的颜色总数最少。
1.2设计要求
(1)设计该问题的核心算法;
(2)设计可视化的界面,界面中能显示和区分中国地图中各省、市、自治区;
(3)程序能正确对地图着色。
2.方法及基本思路
本题抽象出来其实就是着色问题:已知一个图,要求给图上每个点上色,并保证该点的颜色与它的邻接点的颜色都不相同。
回溯法的基本思想是:在解空间中,按深度优先策略,从根结点出发搜索,搜索至任一节点时,先判断该节点是否包含问题的解。如果不包含,则跳过以该节点为根的子节点,逐层向其父节点回溯。否则,进入该子树,继续按照深度优先策略搜索。
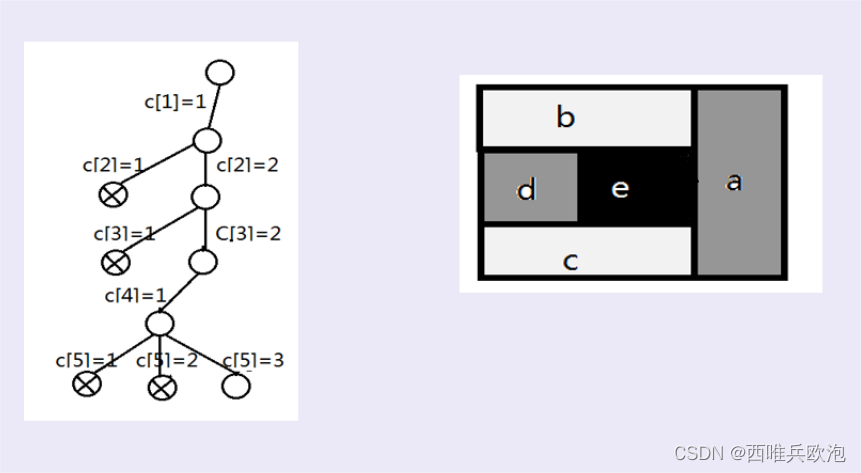
假设地图邻接关系如右所示,那么它的状态解空间树如左图所示:
3.算法描述
算法名称:回溯法
输入:34个省份
输出:每个省份的颜色
省份着色(Graph) :
1. 初始化变量:
着色颜色数 colorCount = 0
最小着色颜色数 minColorCount = ∞
2. 对于图中的每个省份节点 v,设置其颜色 color[v] = 0
3. 对于图中的每个省份节点 v,将其未使用的颜色 mark[v][c] = true
4. 递归着色(0) // 从第一个省份节点开始着色
5. 输出结果最小着色颜色数 minColorCount
递归着色(v) :
1. 如果当前省份节点 v 是最后一个节点:
更新最小着色颜色数 minColorCount = colorCount
返回
2. 对于每一种颜色 c 从 1 到 maxColors:
If:省份节点 v 可以使用颜色 c:
设置 color[v] = c
对于省份节点 v 的每一个相邻节点 u,更新 mark[u][c] = false
颜色数 colorCount++
递归着色(v + 1)
颜色数 colorCount --
对于省份节点 v 的每一个相邻节点 u,更新 mark[u][c] = true
If: colorCount > minColorCount:
说明当前方案无效,回溯到上一个节点
4.时间空间复杂度分析
基本运算:比较
递归公式:T(N, k) = k * T(N-1, k-1)
时间复杂度:O(k^N)
在最坏情况下,算法需要遍历所有可能的颜色方案,所以时间复杂度为 O(k^N),其中 k 是可用的颜色数,N 是省份节点的数量。
空间复杂度:O(N)
递归调用栈的深度最大为省份节点的数量 N,所以空间复杂度为 O(N)。
5.算法实例
输入数据:输入34个省份以及各省邻接关系
输出数据:如下图,由于C语言不支持可视化,改为用省份颜色表示着色,一共得到四种颜色,且相邻省份颜色不同。
6.源码
参考链接
中国地图着色问题-CSDN博客
这位博主的代码可在Dev C++下运行;以下是我稍作修改,可以在VS2022中运行的代码,并为此添加了注释
#include
#include
#include
#include "string.h"
#include
// 定义一个结构体ArcNode,表示省份之间的连接关系
typedef struct ArcNode {
int apn; // 相邻省的序号,即连接的省份
struct ArcNode* nextarc; // 指向下一个ArcNode的指针,表示下一个连接的省份
} ArcNode;
// 定义一个结构体VNode,表示一个省份的信息
typedef struct VNode {
char name[6];
int color;
int number;
ArcNode* firstarc; // 指向该省份的第一个连接关系的指针
} VNode;
// 定义一个结构体DNode,表示双链表的一个节点
typedef struct DLinkNode {
struct VNode* data; // 指向VNode的指针,作为双链表节点的数据
struct DLinkNode* prior; // 指向前一个DLinkNode的指针
struct DLinkNode* next; // 指向下一个DLinkNode的指针
} DLinkNode;
// 定义一个数组,存储ArcNode的指针,最多可以存储145个省份的连接关系
ArcNode* node[145], * p;
// 定义一个数组,存储VNode的实例,最多可以存储35个省份的信息
VNode province[35];
// 定义一个二维数组,存储每个省份的颜色,最多可以存储35个省份的5种颜色(红、绿、蓝、黄、紫)
int color[35][5];
void Intput(VNode* province, ArcNode* node[]); // 输入中国地图信息的函数,参数是省份和连接关系的数组
void Initialization(VNode* province); // 初始化各省颜色及颜色数组
void Painting(VNode* province, ArcNode* p, int i); // 对省份进行上色的函数,参数是省份和指向某个连接关系的指针和省份的序号
void Setcolor(int i); // 设置输出颜色的函数,参数是颜色编号
void Output(VNode* province, ArcNode* p); 输出信息的函数,参数是省份和指向某个连接关系的指针
void Find(DLinkNode*& L, VNode* province, ArcNode* p); // // 求最少着色颜色的函数,参数是双链表的头节点、省份数组和省份的数量
void CreateListR(DLinkNode*& L, VNode* province, int n); // // 使用尾插法创建双链表的函数,参数是双链表的头节点、省份数组和省份的数量
int main() {
DLinkNode* DuLinkLis; // 双链表的头节点指针
Intput(province, node); // 输入中国地图信息
CreateListR(DuLinkLis, province, 34); // 使用尾插法创建双链表
Find(DuLinkLis, province, p); // 求最少着色颜色数
return 0;
}
// 输入中国地图信息的函数实现
void Intput(VNode* province, ArcNode* node[]) {
for (int i = 1; i nextarc = node[i + 1]; // node[i]->nextarc指向node[i+1],即每个连接关系的下一个连接关系是node[i+1]
strcpy_s(province[1].name, 20,"新疆");
province[1].firstarc = node[1];
node[1]->apn = 2;
node[2]->apn = 3;
node[3]->apn = 4;
node[3]->nextarc = NULL;
strcpy_s(province[2].name, 20,"西藏");
province[2].firstarc = node[4];
node[4]->apn = 1;
node[5]->apn = 3;
node[6]->apn = 7;
node[7]->apn = 8;
node[7]->nextarc = NULL;
strcpy_s(province[3].name, 20,"青海");
province[3].firstarc = node[8];
node[8]->apn = 1;
node[9]->apn = 2;
node[10]->apn = 4;
node[11]->apn = 7;
node[11]->nextarc = NULL;
strcpy_s(province[4].name,20, "甘肃");
province[4].firstarc = node[12];
node[12]->apn = 1;
node[13]->apn = 3;
node[14]->apn = 5;
node[15]->apn = 6;
node[16]->apn = 7;
node[17]->apn = 9;
node[17]->nextarc = NULL;
strcpy_s(province[5].name,20, "内蒙古");
province[5].firstarc = node[18];
node[18]->apn = 4;
node[19]->apn = 6;
node[20]->apn = 9;
node[21]->apn = 13;
node[22]->apn = 21;
node[23]->apn = 32;
node[24]->apn = 33;
node[25]->apn = 34;
node[25]->nextarc = NULL;
strcpy_s(province[6].name, 20,"宁夏");
province[6].firstarc = node[26];
node[26]->apn = 4;
node[27]->apn = 5;
node[28]->apn = 9;
node[28]->nextarc = NULL;
strcpy_s(province[7].name,20, "四川");
province[7].firstarc = node[29];
node[29]->apn = 2;
node[30]->apn = 3;
node[31]->apn = 4;
node[32]->apn = 8;
node[33]->apn = 9;
node[34]->apn = 10;
node[35]->apn = 11;
node[35]->nextarc = NULL;
strcpy_s(province[8].name, 20,"云南");
province[8].firstarc = node[36];
node[36]->apn = 2;
node[37]->apn = 7;
node[38]->apn = 11;
node[39]->apn = 12;
node[39]->nextarc = NULL;
strcpy_s(province[9].name,20, "陕西");
province[9].firstarc = node[40];
node[40]->apn = 4;
node[41]->apn = 5;
node[42]->apn = 6;
node[43]->apn = 7;
node[44]->apn = 10;
node[45]->apn = 13;
node[46]->apn = 14;
node[47]->apn = 15;
node[47]->nextarc = NULL;
strcpy_s(province[10].name, 20,"重庆");
province[10].firstarc = node[48];
node[48]->apn = 7;
node[49]->apn = 9;
node[50]->apn = 11;
node[51]->apn = 15;
node[52]->apn = 16;
node[52]->nextarc = NULL;
strcpy_s(province[11].name,20, "贵州");
province[11].firstarc = node[53];
node[53]->apn = 7;
node[54]->apn = 8;
node[55]->apn = 10;
node[56]->apn = 12;
node[57]->apn = 16;
node[57]->nextarc = NULL;
strcpy_s(province[12].name, 20,"广西");
province[12].firstarc = node[58];
node[58]->apn = 8;
node[59]->apn = 11;
node[60]->apn = 16;
node[61]->apn = 17;
node[61]->nextarc = NULL;
strcpy_s(province[13].name, 20,"山西");
province[13].firstarc = node[62];
node[62]->apn = 5;
node[63]->apn = 9;
node[64]->apn = 14;
node[65]->apn = 21;
node[65]->nextarc = NULL;
strcpy_s(province[14].name,20, "河南");
province[14].firstarc = node[66];
node[66]->apn = 9;
node[67]->apn = 13;
node[68]->apn = 15;
node[69]->apn = 21;
node[70]->apn = 24;
node[71]->apn = 25;
node[71]->nextarc = NULL;
strcpy_s(province[15].name, 20,"湖北");
province[15].firstarc = node[73];
node[73]->apn = 9;
node[74]->apn = 10;
node[75]->apn = 14;
node[76]->apn = 16;
node[77]->apn = 25;
node[78]->apn = 26;
node[78]->nextarc = NULL;
strcpy_s(province[16].name,20,"湖南");
province[16].firstarc = node[79];
node[79]->apn = 10;
node[80]->apn = 11;
node[81]->apn = 12;
node[82]->apn = 15;
node[83]->apn = 17;
node[84]->apn = 26;
node[84]->nextarc = NULL;
strcpy_s(province[17].name,20, "广东");
province[17].firstarc = node[85];
node[85]->apn = 12;
node[86]->apn = 16;
node[87]->apn = 19;
node[88]->apn = 20;
node[89]->apn = 26;
node[90]->apn = 30;
node[90]->nextarc = NULL;
strcpy_s(province[18].name, 20,"海南");
province[18].firstarc = NULL;
strcpy_s(province[19].name,20, "澳门");
province[19].firstarc = node[91];
node[91]->apn = 17;
node[91]->nextarc = NULL;
strcpy_s(province[20].name,20, "香港");
province[20].firstarc = node[92];
node[92]->apn = 17;
node[92]->nextarc = NULL;
strcpy_s(province[21].name,20, "河北");
province[21].firstarc = node[93];
node[93]->apn = 5;
node[94]->apn = 13;
node[95]->apn = 14;
node[96]->apn = 22;
node[97]->apn = 23;
node[98]->apn = 24;
node[99]->apn = 34;
node[99]->nextarc = NULL;
strcpy_s(province[22].name, 20,"北京");
province[22].firstarc = node[100];
node[100]->apn = 21;
node[101]->apn = 23;
node[101]->nextarc = NULL;
strcpy_s(province[23].name,20, "天津");
province[23].firstarc = node[102];
node[102]->apn = 21;
node[103]->apn = 22;
node[103]->nextarc = NULL;
strcpy_s(province[24].name,20, "山东");
province[24].firstarc = node[104];
node[104]->apn = 14;
node[105]->apn = 21;
node[106]->apn = 25;
node[107]->apn = 27;
node[107]->nextarc = NULL;
strcpy_s(province[25].name, 20,"安徽");
province[25].firstarc = node[108];
node[108]->apn = 14;
node[109]->apn = 15;
node[110]->apn = 24;
node[111]->apn = 26;
node[112]->apn = 27;
node[113]->apn = 29;
node[113]->nextarc = NULL;
strcpy_s(province[26].name, 20,"江西");
province[26].firstarc = node[115];
node[115]->apn = 15;
node[116]->apn = 16;
node[117]->apn = 17;
node[118]->apn = 25;
node[119]->apn = 29;
node[120]->apn = 30;
node[120]->nextarc = NULL;
strcpy_s(province[27].name,20, "江苏");
province[27].firstarc = node[122];
node[122]->apn = 24;
node[123]->apn = 25;
node[124]->apn = 28;
node[125]->apn = 29;
node[125]->nextarc = NULL;
strcpy_s(province[28].name,20, "上海");
province[28].firstarc = node[126];
node[126]->apn = 27;
node[127]->apn = 29;
node[127]->nextarc = NULL;
strcpy_s(province[29].name,20, "浙江");
province[29].firstarc = node[128];
node[128]->apn = 17;
node[129]->apn = 25;
node[130]->apn = 26;
node[131]->apn = 27;
node[132]->apn = 28;
node[132]->nextarc = NULL;
strcpy_s(province[30].name, 20,"福建");
province[30].firstarc = node[133];
node[133]->apn = 17;
node[134]->apn = 26;
node[135]->apn = 29;
node[135]->nextarc = NULL;
strcpy_s(province[31].name,20, "台湾");
province[31].firstarc = NULL;
strcpy_s(province[32].name, 20,"黑龙江");
province[32].firstarc = node[136];
node[136]->apn = 5;
node[137]->apn = 33;
node[137]->nextarc = NULL;
strcpy_s(province[33].name,20, "吉林");
province[33].firstarc = node[138];
node[138]->apn = 5;
node[139]->apn = 32;
node[140]->apn = 34;
node[140]->nextarc = NULL;
strcpy_s(province[34].name, 20,"辽宁");
province[34].firstarc = node[141];
node[141]->apn = 5;
node[142]->apn = 21;
node[143]->apn = 33;
node[143]->nextarc = NULL;
}
// 初始化函数,对省份数组进行初始化
void Initialization(VNode* province) {
// 循环遍历34个省份
for (int i = 1; i prior = L->next = NULL;
// 设置头结点的数据为省份数组的第一个省份的信息
L->data = &province[1];
// r指针始终指向双链表的终端结点,开始时指向头结点
r = L; //r始终指向终端结点,开始时指向头结点
// 循环创建双链表的结点,从第二个省份开始,直到第n个省份
for (int i = 2; i data = &province[i];
// 将新结点插入到r指针指向的结点之后
r->next = s; s->prior = r; //将结点s插入结点r之后
// r指针指向新插入的结点
r = s;
}
// 将双链表的尾结点的next指针指向头结点,形成环状结构
r->next = L; //尾结点next域置为头节点
// 将头结点的prior指针指向尾结点,形成环状结构
L->prior = r;
}
void Painting(VNode* province, ArcNode* p, int i) {
// 将p指向province数组中第i个省份的第一个邻接省份
p = province[i].firstarc;
// 遍历该省份的所有邻接省份
while (p != NULL)
{
// 根据邻接省份的颜色值进行判断和操作
switch (province[p->apn].color)
{
// 如果邻接省份的颜色值为1,则将当前省份的第0列颜色值设为0 (第一种颜色为0已经使用,不再可用)
case 1:color[i][0] = 0; break;
// 如果邻接省份的颜色值为2,则将当前省份的第1列颜色值设为0
case 2:color[i][1] = 0; break;
// 如果邻接省份的颜色值为3,则将当前省份的第2列颜色值设为0
case 3:color[i][2] = 0; break;
// 如果邻接省份的颜色值为4,则将当前省份的第3列颜色值设为0
case 4:color[i][3] = 0; break;
// 如果邻接省份的颜色值为5,则将当前省份的第4列颜色值设为0
case 5:color[i][4] = 0; break;
// 如果邻接省份的颜色值不在1-5之间,不进行任何操作
default:break;
}
// 移动到下一个邻接省份
p = p->nextarc;
}
// 在当前省份可能被分配的5种颜色中,找出第一个非零颜色值并分配给当前省份
for (int j = 0; j prior) // 当s不等于其前驱节点时,执行循环。
{
Painting(province, p, s->data->number); // 调用Painting函数,传入省份数组、弧节点数组和当前节点的编号,对地图进行着色。
if (s->data->color > Maxcolor) // 如果当前节点的颜色大于Maxcolor。
if (s->data->number != r->data->number) // 如果当前节点的编号不等于r节点的编号。
{
s->data->color = 0; // 将当前节点的颜色设置为0。
for (int j = 0; j data->number][j] = j + 1;
s = s->prior; // 将s指向其前驱节点。
goto a; // 跳转到标签a。
}
else // 如果当前节点的编号等于r节点的编号。
{
printf("从第%d个省%s开始着色用%d种颜色着色失败\n", r->data->number, r->data->name, Maxcolor); // 打印失败信息。
Maxcolor++; // 将Maxcolor增加1。
Initialization(province); // 重新初始化省份数组。
s = r; // 将s指向r。
goto a; // 跳转到标签a。
}
if (s->data->number == r->prior->data->number) // 如果当前节点的编号等于r的前驱节点的编号。
{
printf("从第%d个省%s开始着色用%d种颜色着色成功", r->data->number, r->data->name, Maxcolor); // 打印成功信息。
if (Maxcolor next; // 将s指向其下一个节点。
a:; // 标签a,表示跳转点。
}
b: r = r->next; // 标签b,将r指向其下一个节点。继续下一次循环。
} while (r != L); // 当r不等于L时,继续循环。循环结束条件是r等于L。
Setcolor(4); // 设置文本颜色为4。
printf("\n对中国地图最少着色颜色数为%d种!!\n", Mincolor); // 打印最少需要的颜色数。
Setcolor(8); // 设置文本颜色为8,恢复默认颜色。
return;
}