2023年第十四届蓝桥杯JavaB组省赛真题及全部解析(上)
目录
前言:
一、试题 A:阶乘求和(填空)
二、试题 B:幸运数字(填空)
三、试题 C:数组分割
四、试题 D:矩阵总面积
五、试题 E:蜗牛
六、试题 F:合并区域
前言:
这一篇是我蓝桥系列的第一篇,当然现在第十五届蓝桥杯已经打完了,作者也有参加,运气比较好,拿了个国二,虽然没有达到自己的预期,但也是完成学校的任务,作者是福建省的(弱省),省一我觉得还是挺简单的,随便 ac 两题,打打暴力就省一了,排名还很靠前。蓝桥杯的含金量肯定是不如 ICPC(ACM)和 CCPC (中国的ACM),这个我是深有体会,因为我有参加 CCPC 福建省邀请赛(福州大学),暴零了(一题都没有做出来),直接去旅游了😭😭😭。只能说那种级别的比赛真不是一般人能打的。接下来我会分享我备赛蓝桥杯过程刷的真题和解析,方便和我一样第一次参加蓝桥杯的小白备赛。由于题目比较多,后面几题的题解比较长,只能分成两篇来发,如果有需要的话可以点开下部分,讲解了第 7 到第 10 题。
题目来自:蓝桥杯官网
一、试题 A:阶乘求和(填空)
• 题目分析:
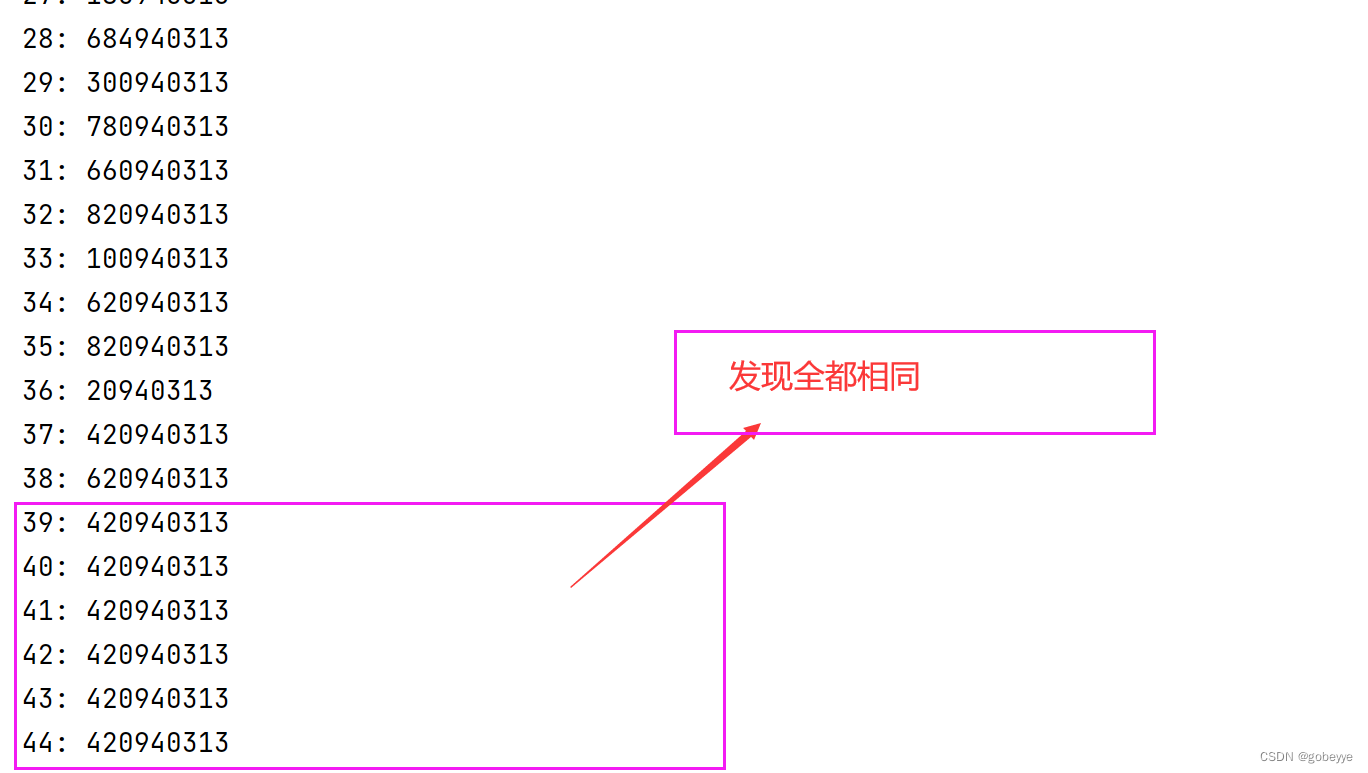
在这里先提醒大家一下,填空题做不出来很正常,我当时填空题第一题也没做出来(就是有点影响心态)。看到这个题,202320232023 这个数的阶乘是不能开 BigInteger 的(这个数非常大),会爆掉的,且这么大的数,在比赛时间内都不一定能跑完。所以我们只能找规律,比赛的时候找不出来的话,可以先把 1 到 50 的结果打印出来。说不定就能找到规律,直接使用计算器算(可以使用计算器)。下面就是就是第 i 阶乘的后 9 位,要取模不然 long 存不下,比赛发现这个规律就可以填了(要珍惜时间)。
• 解题思路:
我们可以观察到当阶乘的底数大于等于 5 时,阶乘结果的末尾将开始出现 0。这是因为阶乘结果中含有至少两个因子 2 和 5,而 2 和 5 相乘正好为 10(结尾就会出现 0 )。
在一个正整数阶乘的时候,因子 2 的个数一定不小于因子 5 的个数,因此我们只需要考虑因子 5 的个数即可。当因子 5 的个数大于等于 9 时,这个阶乘的后面 9 位就都为 0 了,因此这个阶乘后面就不用再考虑了。
我们可以看到在正整数中因子为 5 出现在 5,10,15,20,25(可以算两个),30,35,40,45.....而我们只要前面 9 个即可,也就是 40 之前。当阶乘数大于等于 40 时,结尾 9 位数都是0.
因此本题其实只要计算前 40 个阶乘之和。从 40!开始以后都不会影响到最终的结果。
注意:在运算的过程中要取模防止溢出(MOD取 1e9 即可,正好是后面 9 位)。
• 代码编写:
public class Main {
public static void main(String[] args) {
int MOD = (int) 1e9;
long sum = 0;//保存和
long mul = 1;
for (int i = 1; i
• 运行结果:
二、试题 B:幸运数字(填空)
• 题目分析:
不要被题目吓到了,读过题目就会发现这是一道签到题,2023 也不会很大。
• 解题思路:
按照题目的意思模拟即可。
• 代码编写:
binary是求出 n 在 base 进制下的各位数和。
public class Main {
public static void main(String[] args) {
int count = 0;
for(long i = 1;;i++){
if(i % binary(i,2) == 0 && i % binary(i,8) ==0 && i % binary(i,10) == 0
&& i % binary(i,16) == 0){//根据题意模拟
count++;
}
if(count == 2023){
System.out.println(i);
return;
}
}
}
public static int binary(long n,int base){//求出 n 在 base 进制下的各位数和
int sum = 0;
while(n > 0){
sum += n % base;
n /= base;
}
return sum;
}
}
• 运行结果:
三、试题 C:数组分割
由于题目加上输入各式和输出格式比较长,需要的友友自行去官方那里看就行。
• 题目分析:
题目简单可以理解为:将一个数组分为两个偶数数组(0 也是偶数)。根据数学性质,两个偶数相加的和一定也为偶数,因此如果给出的数组总和不是偶数的话直接打印 0 即可。直接讨论两组数组的所有情况非常麻烦。考虑到总和已经为偶数,因此我们只需找出其中 1 个数组的总和为偶数(另一个数组一定也是偶数)的所有情况,就是我们的最终答案。最终这个问题就转化成了类似 01 背包问题,从 1 到 n 的数中选,总和为偶数的有多少种情况。
• 解题思路:
这是一道动态规划题,我们要先定义出状态表示。
1. 状态表示:
f[i]:表示在前 i 个数中选,总和为偶数的所有情况个数。
g[i]:表示在前 i 个数中选,总和为奇数的所有情况个数。
2. 状态转移方程:
我们以最后一个位置的元素 a[i] 来研究。
(1)当 a[i] 为偶数时:
f[i]:可以从前 i - 1 个数的所有,和为偶数的方案中(选或者选 a[i])转移过来。
g[i]:可以从前 i - 1 个数的所有,和为奇数的方案中(选或者不选 a[i])转移过来。
故在 a[i] 为偶数的状态转移方程为:
f[i] = 2 * f[i - 1];
g[i] = 2 * g[i - 1];
(2)当 a[i] 为奇数时:
f[i]:可以分别从前 i - 1 个数的所有,和为偶数的方案中(不选 a[i])、前 i - 1 个数的所有,和为奇数的方案中(选 a[i])转移过来。
g[i]:可以分别从前 i - 1 个数的所有,和为偶数的方案中(选 a[i])、前 i - 1 个数的所有,和为奇数的方案中(不选 a[i])转移过来。
f[i] = f[i - 1] + g[i - 1];
g[i] = f[i - 1] + g[i - 1];
3. 初始化
因为数组为空时也算一个偶数方案。所以设 f[0] = 1即可。
• 代码编写:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int MOD = (int) 1e9 + 7;
//dp
int T = in.nextInt();
while (T > 0) {
int n = in.nextInt();
int[] nums = new int[n + 1];
long sum = 0;
for (int i = 1; i