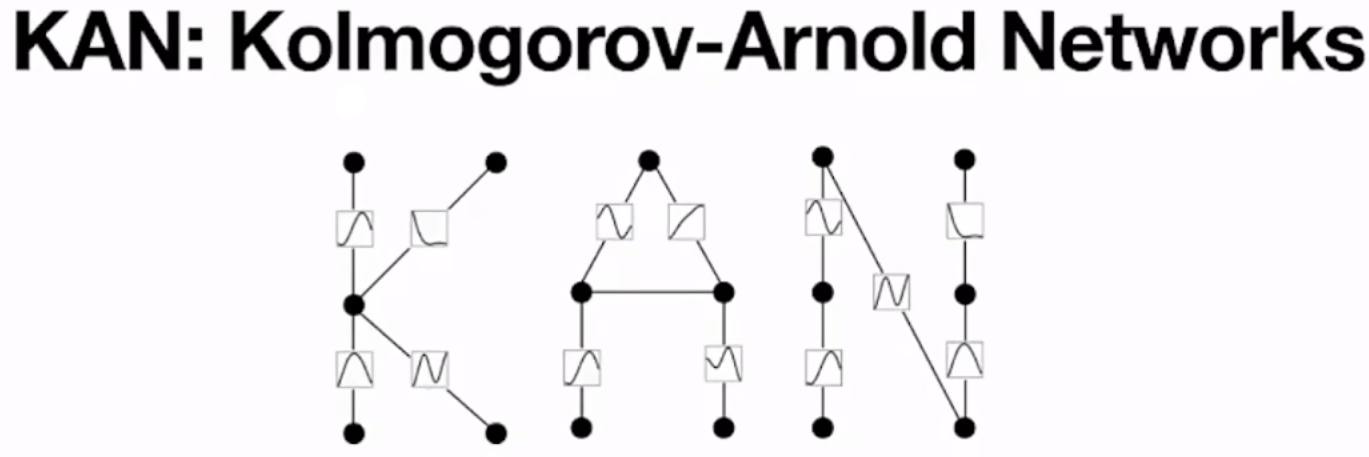
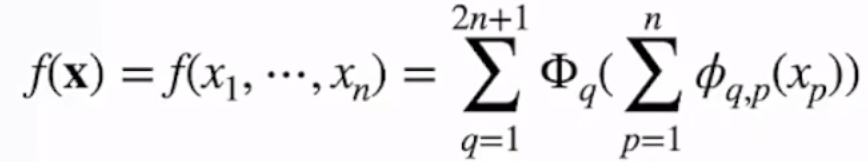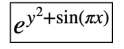一文白话搞懂【KAN】网络，真有那么神奇？

良心总结，白话搞懂【KAN】网络，神奇但没有那么神奇。

论文url：“https://arxiv.org/abs/2404.19756”

github url：“https://github.com/KindXiaoming/pykan”

B站相关视频：

BV1gz421m7ds 【录制】KAN网络作者学术分享会

BV1Hb421b72f 【AI大讲堂： 专业拆解 KAN网络】

目录

• 简单总结
• • KAN与MLP区别
  • KAN网络解析
  • • 怎么来的
    • 激活函数参数化（B-splines）
    • 可解释性
    • 训练过程
    • 总结（Takeaways）

       

      简单总结

      KAN最近被许多媒体吹捧，甚至说要干掉MLP。。

      

      为什么这么多人追捧KAN，因为他提出了一种不同与现在AI大厦基石（感知机，MLP）的全新AI架构，这种有可能颠覆AI发展的发现无疑让人兴奋，或许能给发展十几年沉闷的深度学习世界带来一丝变革的曙光。（也许也是更多人发现了水论文的点，KAN+XXX）。KAN的优势声称是能以更少的参数量实现更高的精度，且有非常好的可解释性。

      那KAN有没有这么神奇，真的是从石头里蹦出来的一个全新架构？ 在比较详细了解KAN后我觉得有必要出一篇文章。本文告诉你答案，没有那么神奇。下面会通俗讲解KAN的细节，pros and cons。

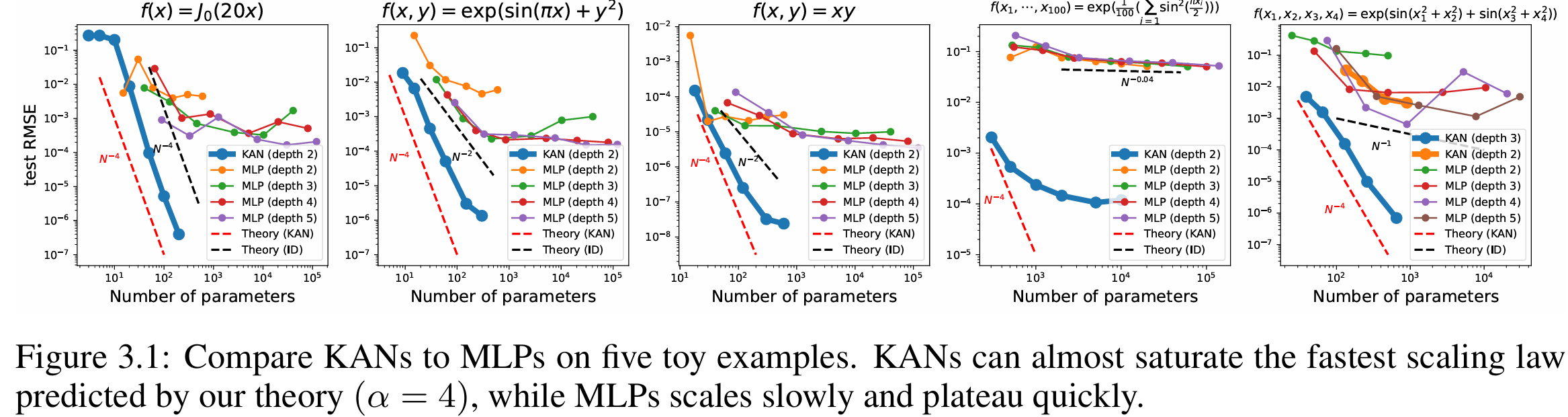
      比较有争议的一个结果图：

      这个结果图也是公众号大肆宣扬的点：200参数量顶30万。。。

      

      作者在交流会中也表示确实论文的benchmark不严谨，MLP没有经过公平设计，其实更小的2层MLP也能达到80%精度。 大家对待公众号的内容一定地辩证看待。

       

      KAN与MLP区别

      一句话可以讲明白：

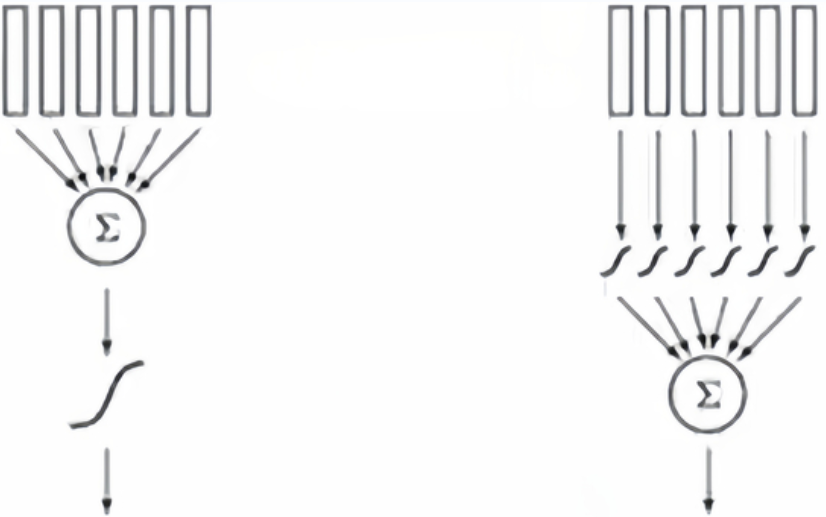
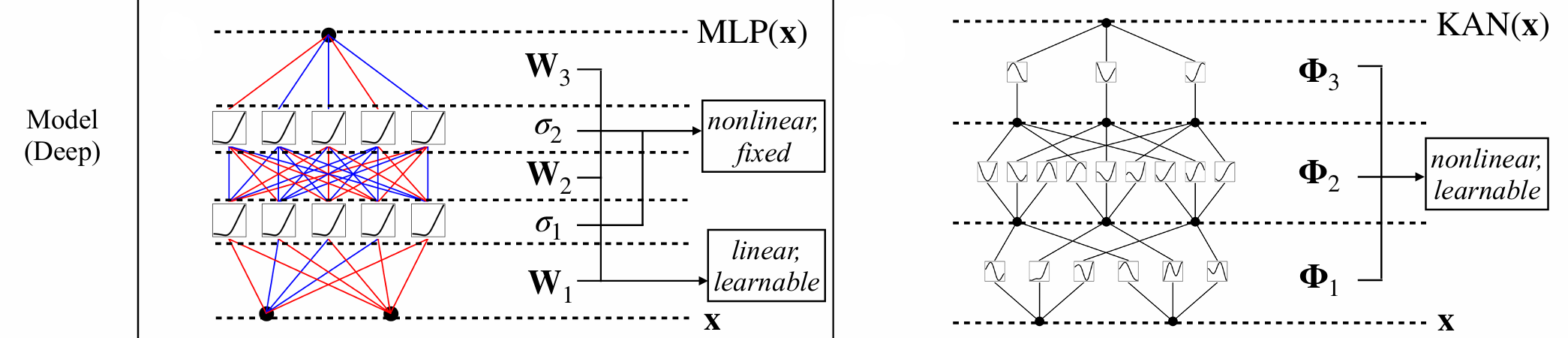
      MLP：线性组合，非线性激活

      KAN：非线性激活（每个输入），线性组合

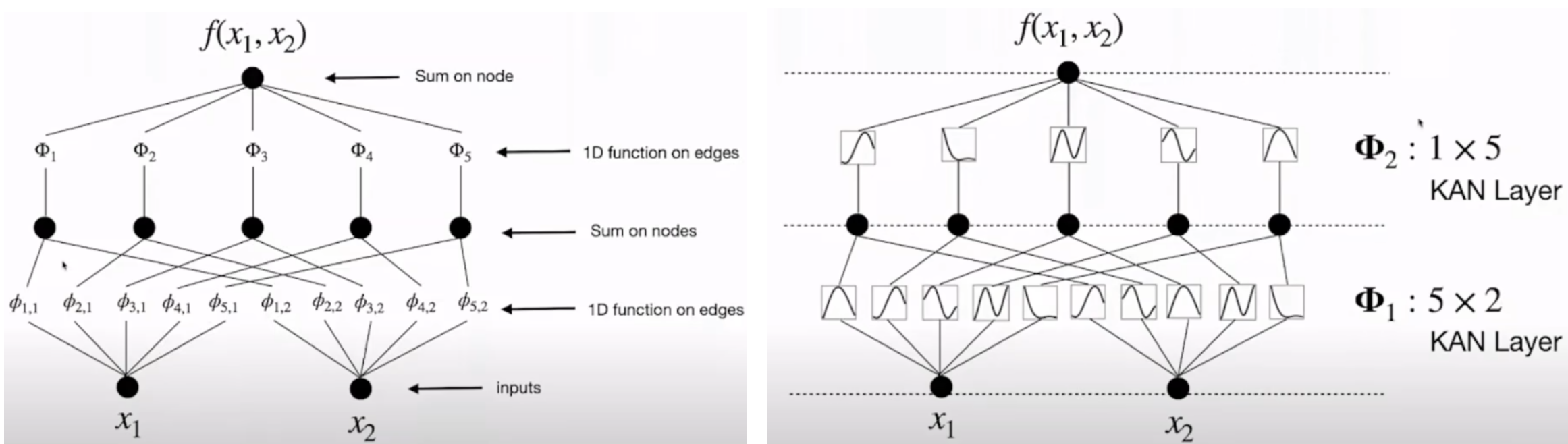
      可以理解为顺序换了一下，下图左边是MLP，右边是KAN，很好理解。最大的点是激活函数不再是固定的Sigmoid或ReLU，它被参数化了，可学！

      

      通俗点理解，

      MLP学习画直线，然后求和进行非线性激活；

      KAN学习画曲线，然后求和；

      曲线表征能力远超直线，所以需要曲线的数量超低于直线的数量。

      所以KAN的优势声称是能以更少的参数量实现更高的精度。

       

      KAN网络解析

      怎么来的

      作者说是启发自一个定理，这也是KAN中KA的来源：Kolmogorov-Arnold 表示定理，不用记住这些人名，下面公司看着复杂其实也很简单，

      

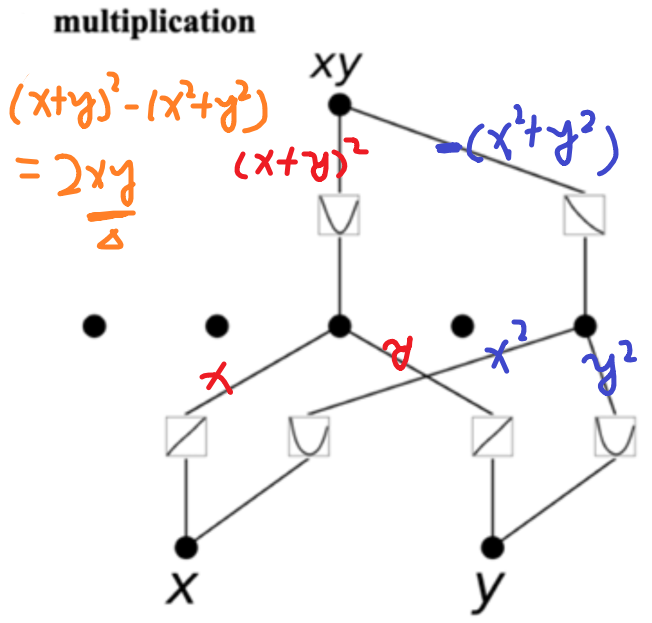
      就是f是一个多元函数（有多个x变量，吐出来一个数），可以被表示为多个单元函数的线性组合，就是单元函数和加法，可以构建出乘法！

      

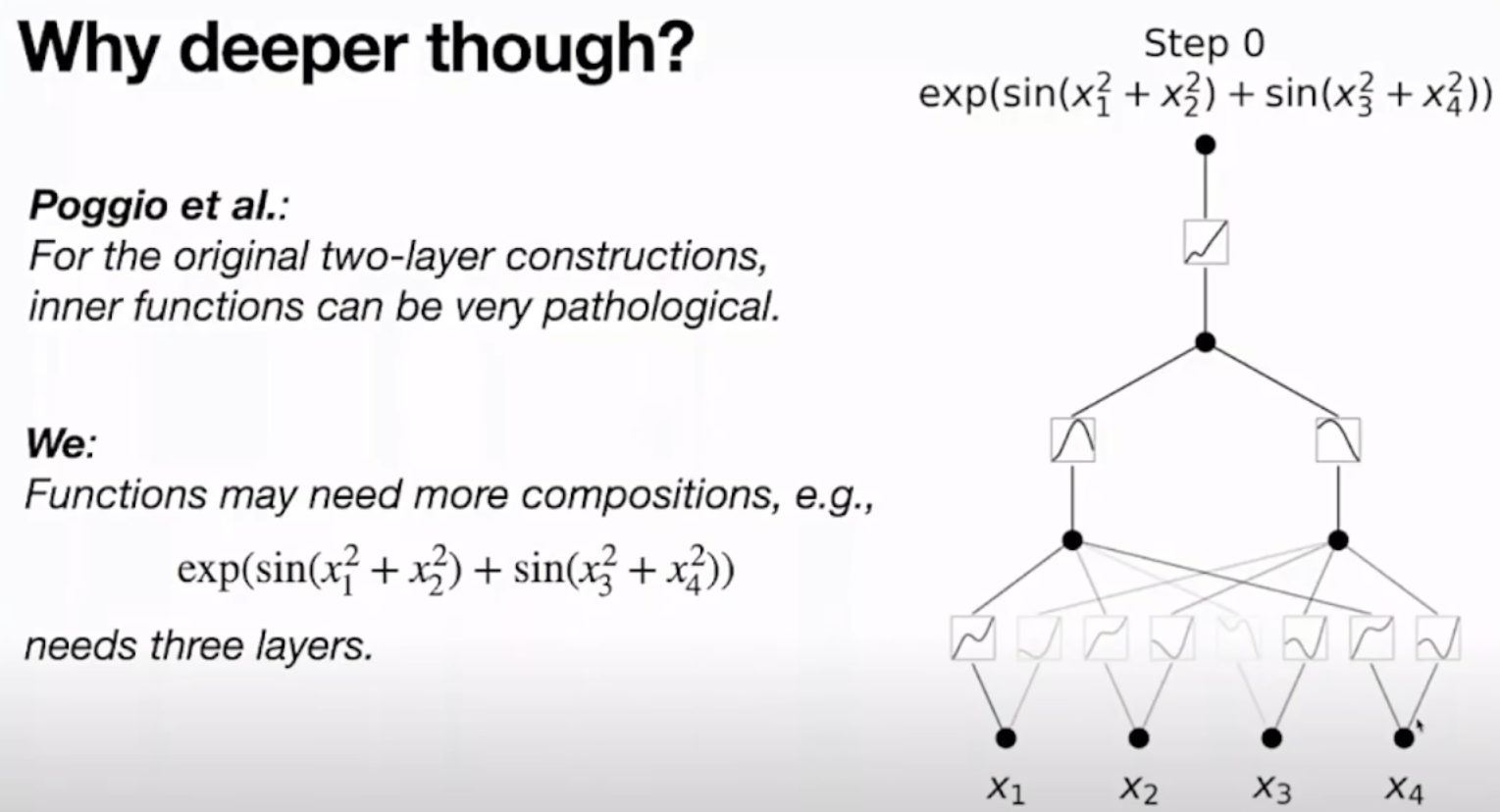
      其实两层理论上可以拟合任何函数，但是激活函数有时会变得非常不光滑，非常病态，才能满足要求，所以这也是多层KAN的必要性。

      

      这也是KAN这篇文章的核心贡献点，它把KA定理改了一下，不局限于每个输入都产生 2n+1个分身（非线性激活），再叠加，本文说KANs可以更灵活，且可以叠加变得deeper，使得激活函数更有现实意义。深度学习（深层）的本质是表征学习（representation learning），核心是compose simple modules to learn complex functions。所以说KANs变多层也符合这一理念。

      

       

      作者自白：

      大家可能很直接想到，为什么不在MLP的节点上将激活函数变得可学？ 这也是作者一开始的思路，但实践下来发现可解释性很差（论文appendix里面有实验）

       

      激活函数参数化（B-splines）

      激活函数所以必须先参数化，才能 learnable。

      作者是选了B样条函数

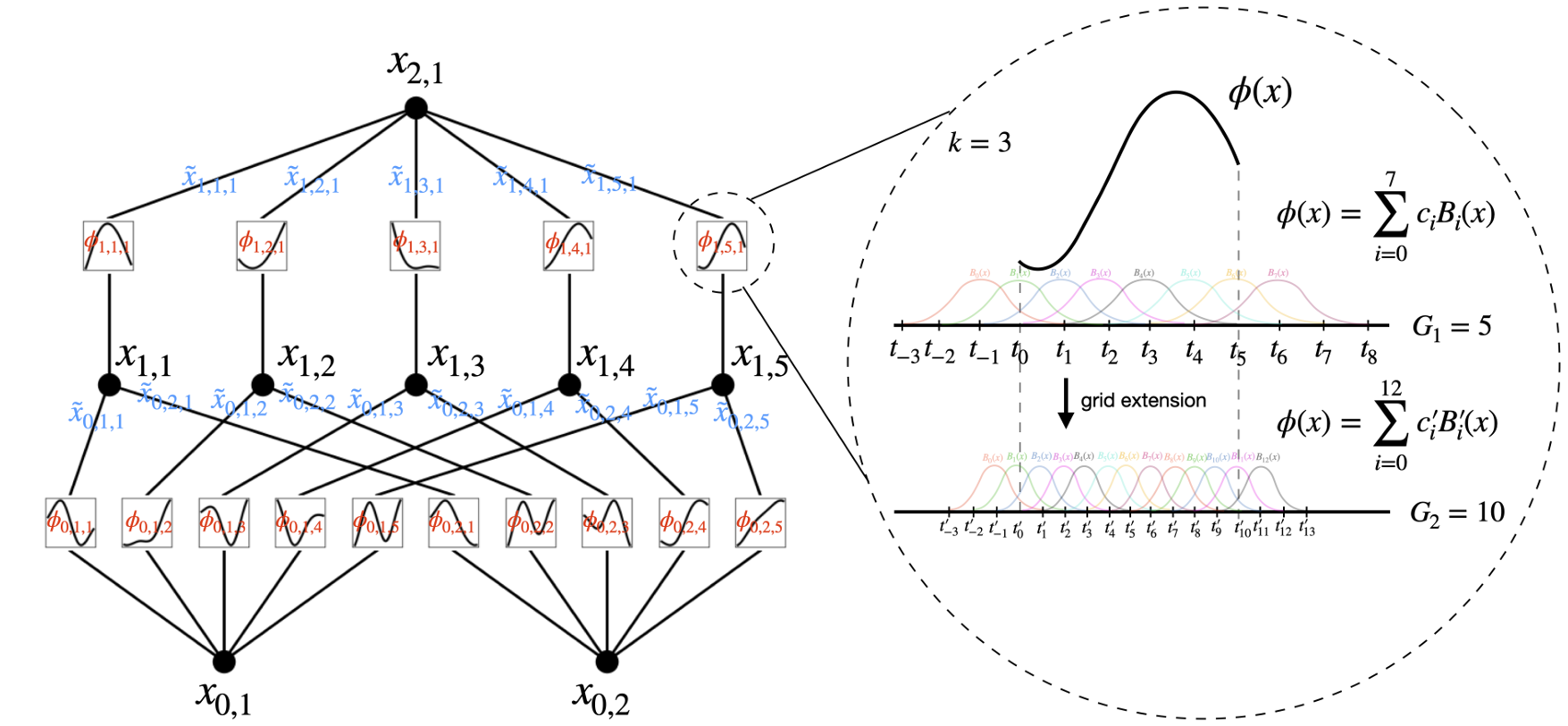
      下图说明了这个样条函数怎么来的：

      

      其实就是多个basic函数的相加，C参数控制每个basic的幅值。Φ函数有粗粒度和细粒度选择，就是选多些basic函数相加就越精准嘛，上图是展示7和12两种情况。G=5表示interval是5.

      

      

       

      具体的可以看文中公式：

      

      

       

      可解释性

       

      

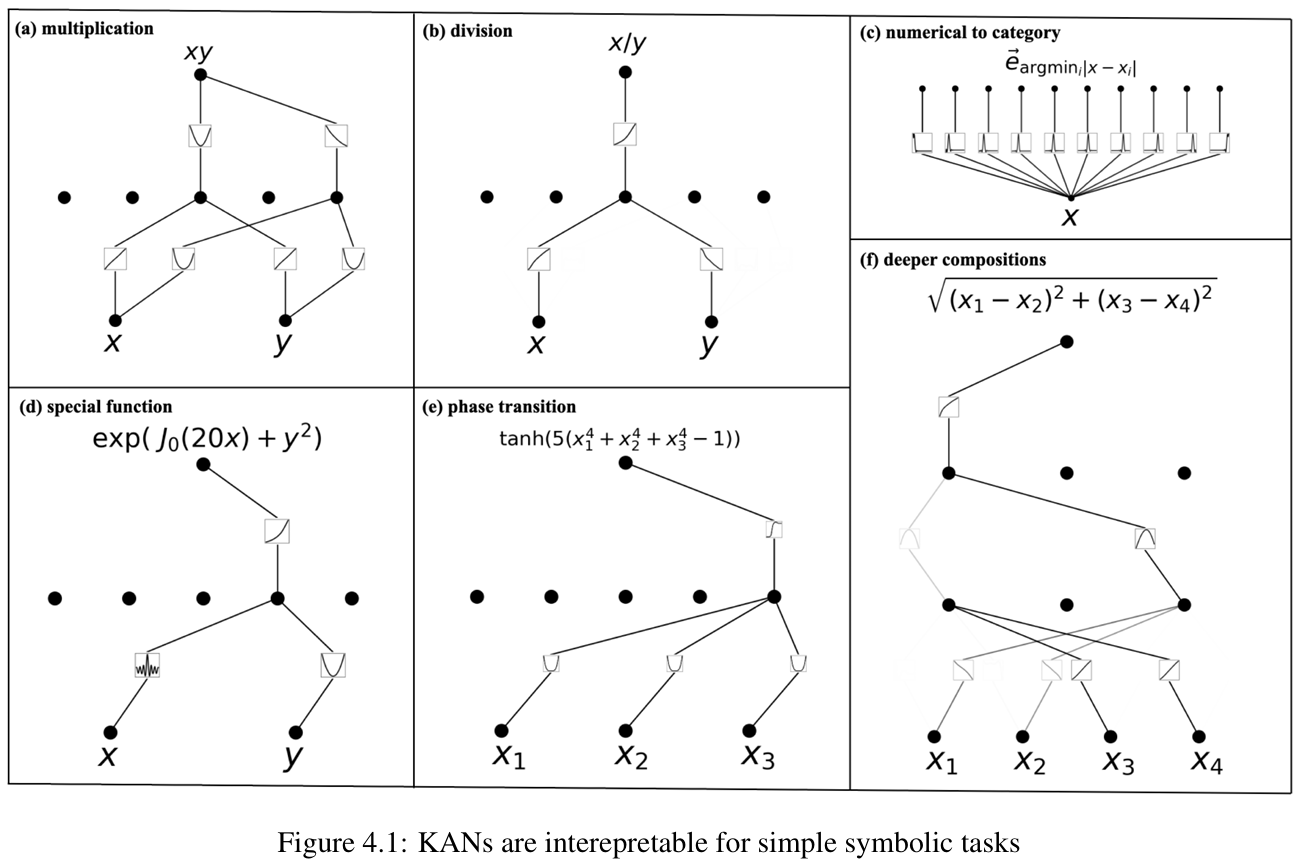
      KAN对符号公式的拟合很promising，且解释性非常好，比如下面的图，网络收敛后，可以从图比较容易读出KAN网络的原理。

      

      下面是论文做的一些公式的拟合，解释性都非常好：

      

       

      且结果表明KAN比MLP在公式拟合方面更高效：

      

       

      训练过程

      KAN比较大的创新是可以在训练过程中加入人类先验的知识，作者表示是更 interactive，更可信.

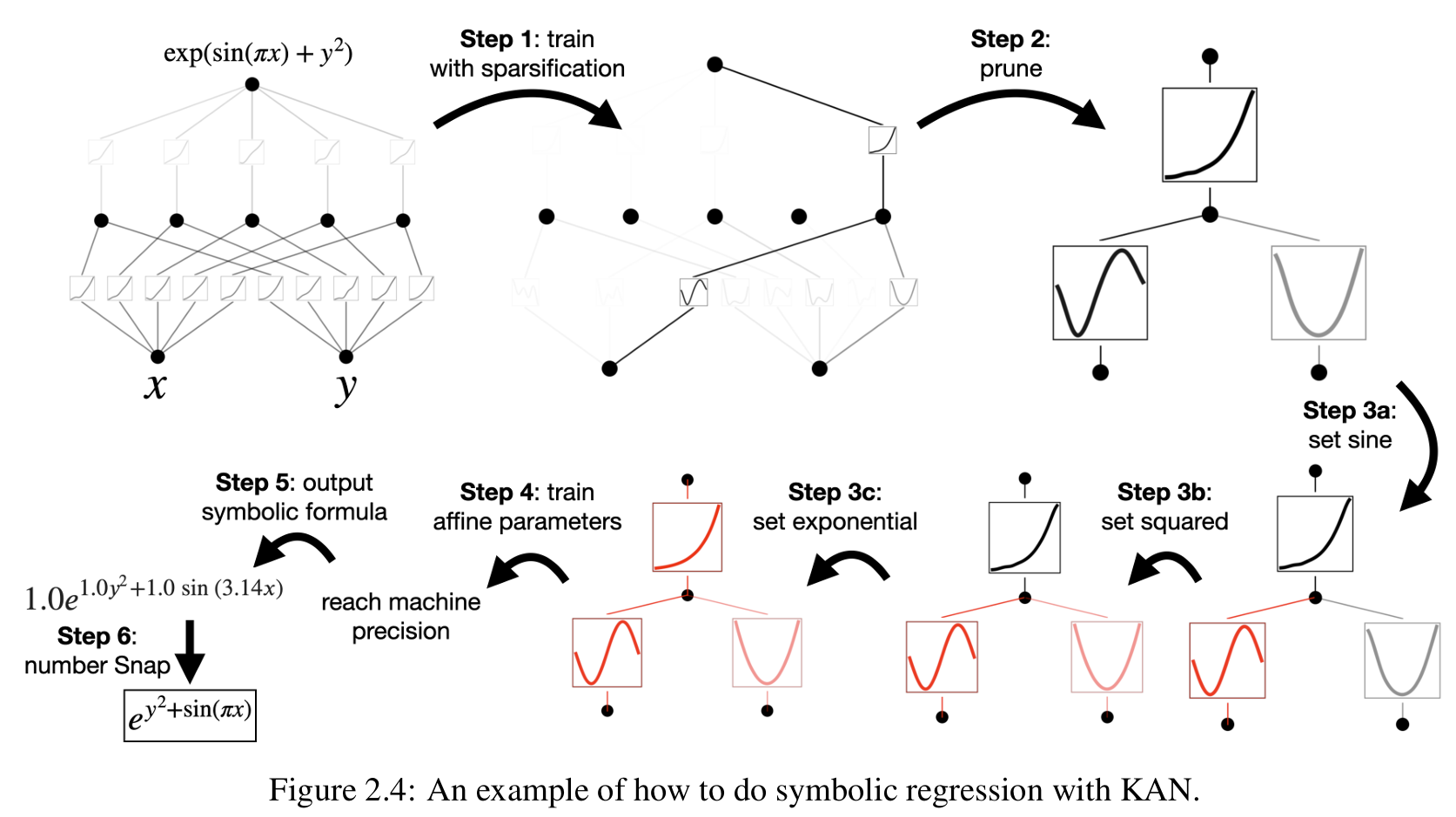
      比如下面这图，在较大的KAN训练完后，进行剪枝（可解释性更高），然后可以人为手动地把激活函数设置为经典的函数（正弦、平方、指数），从而得到一个可信的可解释的直观的表达结果。

      

       

      

      KAN 训练算法：通过 grid extension，也就是激活函数分辨率提升，以及稀疏化、剪枝等结构自优化技巧,实现了准确性和可解释性的提升。能够在参数量大大减少的情况下实现相同甚至更有的拟合效果。

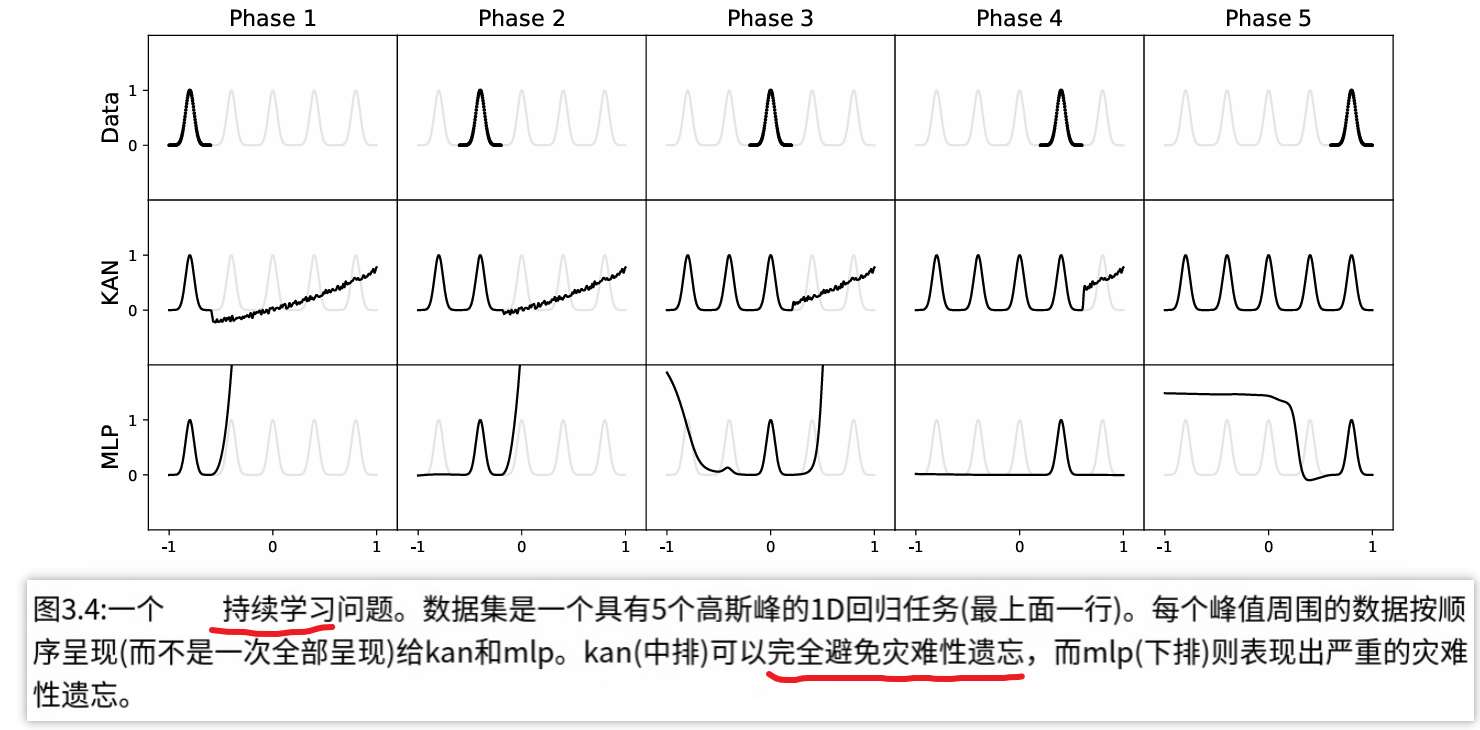
      还有，KAN有比较好的抗遗忘特性！这对于大模型来说很有前景。

      

       

      总结（Takeaways）

      KAN想法没有很颠覆性，大家觉得很厉害只是被传统感知机架构观念植入太深，其实ML领域也还是有其他group在研究别的架构。

      

      如作者说讲，可学的激活函数，在edge加激活函数，多层，这三个概念都有前人研究过，KAN的贡献是将它们整合在一起（bridge gaps），实现 多层的支持edge激活函数可学的全新架构。

      KAN目前主要是在AI4Science上（数学，物理），作者也只是验证了函数拟合，偏微分方程求解等小型science任务方面KAN的好处，至于在我们关注的CV、NLP应用上作者没有验证，应该现在有很多人已经做了实验，发现效果好像没有MLP好，这也很显然，一个刚出生的婴儿怎么可能全方位吊打经过多年迭代更新的传统AI。KAN目前训练速度慢是论文中说明的也是大家直接发现的主要瓶颈。且单看一个KAN和MLP模块，KAN的参数量是要更多的，只是说在某些任务KAN可能可以更少的层实现高精度，所以在小任务上目前还是MLP占优。

      总的来说KAN为AI发展提供了一条新的道路，还很年轻，但前程似锦，用于ML与MLP对飚还需要相当多的优化和验证，比如激活函数应该有比B-splines更好的选择，数学方面只是蹭了一下KA定理，给定理考虑深层情况会让KAN数学基础更强。KAN与MLP结合也完全可以，各取所长。