c语言二叉树的层次遍历（超详细）学习笔记

06-01 1371阅读

 前言：

我学习数据结构的方式是看书加看视频，视频看的是哔哩哔哩up主的 二叉树的层次遍历 我总结并补充他所讲的内容，他的视频适合有c语言基础的看。本文章继我的上一篇文章  c语言二叉树的创建与前序、中序、后序遍历（超详细）学习笔记 ,在二叉树的前序、中序、后序的三种遍历上，继续详细解释二叉树的层次遍历。看完此片文章，一定会有所收获的！

思路：

若想实现层次遍历，那么应该是先遍历根节点A，然后遍历它的左子树B，再遍历它的右子树C，再遍历B的左子树，再遍历B的右子树...

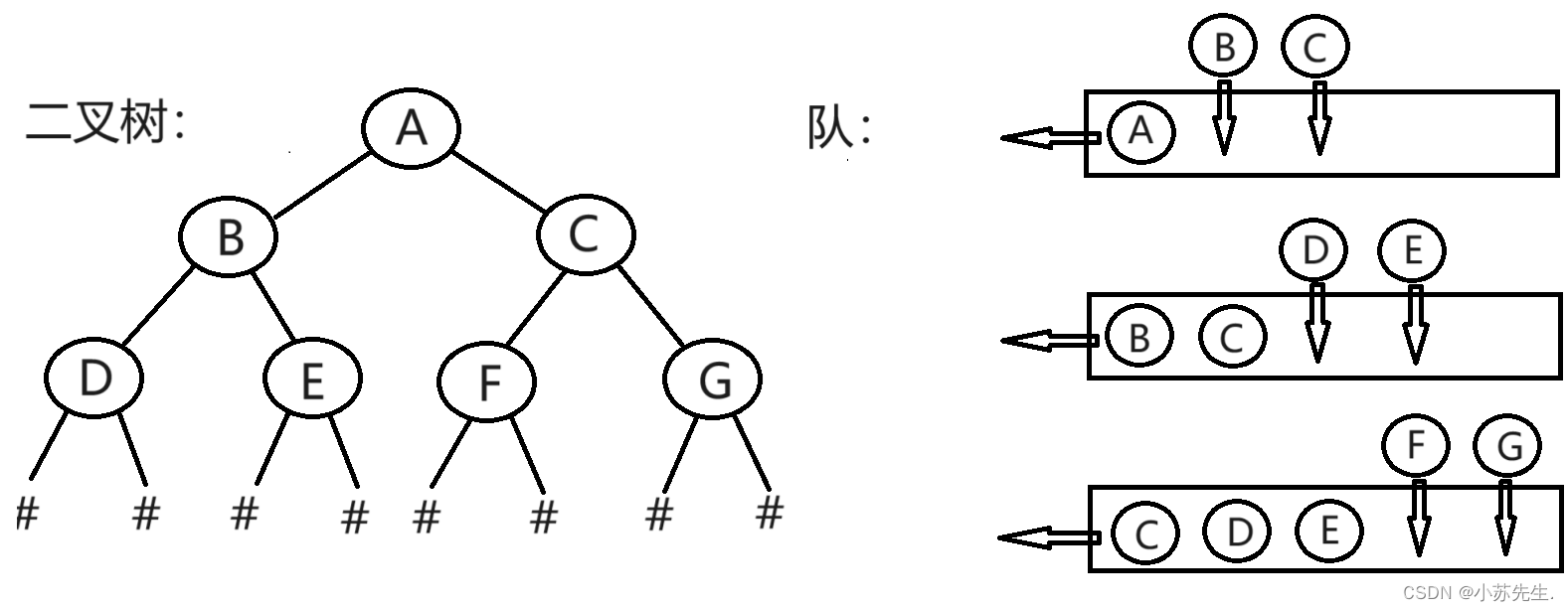
按照这个逻辑关系，我们可以运用树+队的形式，树的结点作为队的元素。

每次入队一个树结点，进行遍历，出队，然后再在将这个树结点的左孩子和右孩子进行入队,依次进行...最终得到层次遍历：A B C D E F G

c语言二叉树的层次遍历（超详细）学习笔记

一、创建树结构体

//创建树结构体
typedef struct TreeNode
{
    char data;
    struct TreeNode* lChild;
    struct TreeNode* rChild;
}treeNode;

二、创建循环队列结构体（链式存储方式）

循环队列的解释：

队的特点是先进先出，循环队列适应两种存储结构，顺序存储有队满情况，链式存储不存在队满情况。因为是链式存储方式，所以不能通过顺序存储中的real和front来判断队空，通过链式结构中的指针域来联系队中的元素彼此。

那么就有两种循环方式：单循环队列和双循环队列方式。所以我会展示两种方式。当然两种方法各有所爱了，总体上是差不多的。

（1）创建单循环队列

//创建循环队列结构体
typedef struct QueueNode
{
    treeNode* data;树的结点作为元素
    struct QueueNode* next;
}QueueNode;

（2）创建双循环队列

//创建双循环队列结构体
typedef struct QueueNode
{
    treeNode* data; //树的结点作为元素
    struct QueueNode* next;
    struct QueueNode* pre;
}QueueNode;

三、初始化二叉树

仍是使用先序方式进行传入数据 并运用递归。如果想了解递归详细的推导，可以看看我的这篇文章 c语言二叉树的创建与前序、中序、后序遍历（超详细）学习笔记

//初始化二叉树
TreeNode* creatTree()
{
    TreeNode* T;
    char ch;
    scanf_s("%c", &ch);//通过输入的ch是否是‘#’来判断该节点是否有孩子节点
    if (ch == '#') //'#'代表传入的是空结点
    {
        //此时为空结点
        return NULL;
    }
    else
    {
        //不为空
        T = (TreeNode*)malloc(sizeof(TreeNode));
        T->data = ch;
        //创建左子树，逻辑一致，进行递归
        T->lChild = creatTree();
        //创建右子树，逻辑一致，进行递归
        T->rChild = creatTree();
        return T;
    }
}

四、创建空队

（1）单循环队列：

//创建空队
QueueNode* initQueue()
{
    QueueNode* Q = (QueueNode*)malloc(sizeof(QueueNode));
    Q->data = NULL;
    Q->next = Q;
    return Q;
}

（2）双循环队列：

//创建空队
QueueNode* initQueue()
{
    QueueNode* Q = (QueueNode*)malloc(sizeof(QueueNode));
    Q->data = NULL;
    Q->next = Q;
    Q->pre = Q;
    return Q;
}

五、入队  （尾插法入队）

尾插法入队的解释：先进先出，方便出队时快速找到当前元素，Q->next == 出队的元素 

如：按照1，2，3，4，5的顺序入队，那么出队的顺序为1，2，3，4，5

头插法入队：Q->1->2->3->4->5，若想出队1，需找到元素1 即：Q->nest == 1，非常快速。

（1）单循环队列：

//入队  尾插法
void enQueue(QueueNode* Q, treeNode* data)
{
    QueueNode* node = (QueueNode*)malloc(sizeof(QueueNode));
    QueueNode* q = Q->next;
    while(q->next != Q)
    { 
        q = q->next;
    }
    node->data = data;
    q->next = node;
    node->next = Q;    
}

（2）双循环队列：

//入队  尾插法
void enQueue(QueueNode* Q, treeNode* data)
{
    QueueNode* node = (QueueNode*)malloc(sizeof(QueueNode));
    node->data = data;
    node->pre = Q->pre;
    node->next = Q;
    Q->pre->next = node;
    Q->pre = node;
}

六、判断队是否为空

//判断队是否为空
int isEmpty(QueueNode* Q)
{
    if (Q->next == Q)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}

七、出队  （头插法出队）

头插法出队，非常快速的找到需要出队的元素，Q->next == 出队的元素

找到出队元素，进行出队操作并返回其元素。

（1）单循环队列：

//出队  头插法
treeNode* deQueue(QueueNode* Q)
{
    if (isEmpty(Q))
    {
        return NULL;
    }
    else
    {
        QueueNode* node = Q->next;
        treeNode* T = node->data;
        Q->next = node->next;
        free(node);
        return T;
    }
}

（2）双循环队列：

//出队  头插法
treeNode* deQueue(QueueNode* Q)
{
    if (isEmpty(Q))
    {
        return NULL;
    }
    else
    {
        QueueNode* node = Q->next;
        treeNode* T = node->data;
        Q->next = node->next;
        node->next->pre = Q;
        free(node);
        return T;
    }
}

八、层次遍历

//层次遍历
void levelTraverse(QueueNode* Q, treeNode* T)
{
    //先进队
    enQueue(Q, T);
    while (!isEmpty(Q))
    {
        treeNode* node = deQueue(Q);
        //将node 进行遍历
        printf("%c ", node->data);
        //如果有左孩子
        if (node->lChild)
        {
            enQueue(Q, node->lChild);
        }
        //如果有右孩子
        if (node->rChild)
        {
            enQueue(Q, node->rChild);
        }
    }
}

思路：每次入队一个树结点，出队并取出其元素，进行遍历，然后再在将这个树结点的左孩子和右孩子进行入队,依次进行...最终得到层次遍历：A B C D E F G

c语言二叉树的层次遍历（超详细）学习笔记

九、前序遍历

//前序遍历   根 左 右
void preOrder(treeNode* T)
{
    if (T == NULL)
    {
        return;
    }
    else
    {       //先办事
        printf("%c ", T->data);
        //左孩子                                    
        preOrder(T->lChild);
        //右孩子                                    
        preOrder(T->rChild);
    }
}

十、完整代码

(1)单循环队列完整代码：

#include
#include
//创建树结构体
typedef struct TreeNode
{
    char data;
    struct TreeNode* lChild;
    struct TreeNode* rChild;
}treeNode;
//创建循环队列结构体
typedef struct QueueNode
{
    treeNode* data;树的结点作为元素
    struct QueueNode* next;
}QueueNode;
//初始化二叉树
TreeNode* creatTree()
{
    TreeNode* T;
    char ch;
    scanf_s("%c", &ch);//通过输入的ch是否是‘#’来判断该节点是否有孩子节点
    if (ch == '#') //'#'代表传入的是空结点
    {
        //此时为空结点
        return NULL;
    }
    else
    {
        //不为空
        T = (TreeNode*)malloc(sizeof(TreeNode));
        T->data = ch;
        //创建左子树，逻辑一致，进行递归
        T->lChild = creatTree();
        //创建右子树，逻辑一致，进行递归
        T->rChild = creatTree();
        return T;
    }
}
//创建空队
QueueNode* initQueue()
{
    QueueNode* Q = (QueueNode*)malloc(sizeof(QueueNode));
    Q->data = NULL;
    Q->next = Q;
    return Q;
}
//入队  尾插法
void enQueue(QueueNode* Q, treeNode* data)
{
    QueueNode* node = (QueueNode*)malloc(sizeof(QueueNode));
    QueueNode* q = Q->next;
    while(q->next != Q)
    { 
        q = q->next;
    }
    node->data = data;
    q->next = node;
    node->next = Q;    
}
//判断队是否为空
int isEmpty(QueueNode* Q)
{
    if (Q->next == Q)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}
//出队  头插法
treeNode* deQueue(QueueNode* Q)
{
    if (isEmpty(Q))
    {
        return NULL;
    }
    else
    {
        QueueNode* node = Q->next;
        treeNode* T = node->data;
        Q->next = node->next;
        free(node);
        return T;
    }
}
//层次遍历
void levelTraverse(QueueNode* Q, treeNode* T)
{
    //先进队
    enQueue(Q, T);
    while (!isEmpty(Q))
    {
        treeNode* node = deQueue(Q);
        //将node 进行打印
        printf("%c ", node->data);
        //如果有左孩子
        if (node->lChild)
        {
            enQueue(Q, node->lChild);
        }
        //如果有右孩子
        if (node->rChild)
        {
            enQueue(Q, node->rChild);
        }
    }
}
//前序遍历   根 左 右
void preOrder(treeNode* T)
{
    if (T == NULL)
    {
        return;
    }
    else
    {       //先办事
        printf("%c ", T->data);
        //左孩子                                    
        preOrder(T->lChild);
        //右孩子                                    
        preOrder(T->rChild);
    }
}
int main()
{
    QueueNode* Q = initQueue();
    treeNode* T = creatTree();
    printf("前序遍历：\n");
    preOrder(T);
    printf("\n");
    printf("层次遍历：\n");
    levelTraverse(Q, T);
    printf("\n");
    return 0;
}

(2)双循环队列完整代码：

#include
#include
//创建树结构体
typedef struct TreeNode
{
    char data;
    struct TreeNode* lChild;
    struct TreeNode* rChild;
}treeNode;
//创建双循环队列结构体
typedef struct QueueNode
{
    treeNode* data; //树的结点作为元素
    struct QueueNode* next;
    struct QueueNode* pre;
}QueueNode;
//初始化二叉树
TreeNode* creatTree()
{
    TreeNode* T;
    char ch;
    scanf_s("%c", &ch);//通过输入的ch是否是‘#’来判断该节点是否有孩子节点
    if (ch == '#') //'#'代表传入的是空结点
    {
        //此时为空结点
        return NULL;
    }
    else
    {
        //不为空
        T = (TreeNode*)malloc(sizeof(TreeNode));
        T->data = ch;
        //创建左子树，逻辑一致，进行递归
        T->lChild = creatTree();
        //创建右子树，逻辑一致，进行递归
        T->rChild = creatTree();
        return T;
    }
}
//创建空队
QueueNode* initQueue()
{
    QueueNode* Q = (QueueNode*)malloc(sizeof(QueueNode));
    Q->data = NULL;
    Q->next = Q;
    Q->pre = Q;
    return Q;
}
//入队  尾插法
void enQueue(QueueNode* Q, treeNode* data)
{
    QueueNode* node = (QueueNode*)malloc(sizeof(QueueNode));
    node->data = data;
    node->pre = Q->pre;
    node->next = Q;
    Q->pre->next = node;
    Q->pre = node;
}
//判断队是否为空
int isEmpty(QueueNode* Q)
{
    if (Q->next == Q)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}
//出队  头插法
treeNode* deQueue(QueueNode* Q)
{
    if (isEmpty(Q))
    {
        return NULL;
    }
    else
    {
        QueueNode* node = Q->next;
        treeNode* T = node->data;
        Q->next = node->next;
        node->next->pre = Q;
        free(node);
        return T;
    }
}
//层次遍历
void levelTraverse(QueueNode* Q, treeNode* T)
{
    //先进队
    enQueue(Q, T);
    while (!isEmpty(Q))
    {
        treeNode* node = deQueue(Q);
        //将node 进行遍历
        printf("%c ", node->data);
        //如果有左孩子
        if (node->lChild)
        {
            enQueue(Q, node->lChild);
        }
        //如果有右孩子
        if (node->rChild)
        {
            enQueue(Q, node->rChild);
        }
    }
}
//前序遍历   根 左 右
void preOrder(treeNode* T)
{
    if (T == NULL)
    {
        return;
    }
    else
    {       //先办事
        printf("%c ", T->data);
        //左孩子                                    
        preOrder(T->lChild);
        //右孩子                                    
        preOrder(T->rChild);
    }
}
int main()
{
    int index = 0;
    QueueNode* Q = initQueue();
    treeNode* T = creatTree();
    printf("前序遍历：");
    preOrder(T);
    printf("\n");
    printf("层次遍历：");
    levelTraverse(Q, T);
    printf("\n");
    return 0;
}

十一、运行结果

c语言二叉树的层次遍历（超详细）学习笔记

输入：ABD##E##CF##G##

c语言二叉树的层次遍历（超详细）学习笔记​

总结：

二叉树层次遍历的好处包括：

1.按照层级顺序访问节点：层次遍历可以按照树的层级顺序访问节点，从根节点开始，逐层向下遍历，这样可以更加直观地观察和理解整个二叉树的结构。

2.方便实现广度优先搜索：层次遍历是广度优先搜索（BFS）的一种实现方式。BFS是一种重要的图搜索算法，广泛应用于图的遍历、路径搜索、连通性判断等问题中。层次遍历的结果正好可以按照广度优先搜索的顺序得到。

3.快速查找某一层的节点：对于二叉树层次遍历的结果，每一层的节点都是按照从左到右的顺序排列的。因此，可以直接通过索引或下标的方式快速查找到某一层的节点。这种特性在某些问题中非常有用，比如在二叉树的每一层中查找特定的节点或值。

4.方便处理与层次相关的问题：有些问题与二叉树的层次相关，比如计算二叉树的最大深度、最小深度，判断二叉树是否是完全二叉树等等。通过层次遍历，可以轻松地处理与层次相关的问题，因为遍历的结果已经按照层级顺序排列好了。

总之，二叉树层次遍历可以提供对二叉树结构的直观理解，方便实现广度优先搜索，快速查找某一层的节点，并处理与层次相关的问题。

实现二叉树的层次遍历需要树+队的结合，队是循环队列，那么有单循环队列和双循环队列两种方式进行实现。制作不易，真心想让你懂，还是有不足的地方，望见谅嘞。

VPS购买请点击我

文章版权声明：除非注明，否则均为主机测评原创文章，转载或复制请以超链接形式并注明出处。

相关阅读

目录[+]