matlab-基于Malthus人口预测模型(笔记)
Malthus人口预测模型
P - 人口数量
t - 时间
r - 人口增长率
这个方程的假设体现在:
-
采用指数增长方程形式,呈指数增长趋势。
-
增长率r为正常数,不随时间变化。
-
未考虑人口增长的饱和状态。
-
未考虑出生率、死亡率等人口学参数。
-
未考虑人口增长对资源环境的反馈作用。
-
未考虑经济、政策等外生变量的影响。
-
未考虑战争、灾害等灾变的影响。
-
未考虑人口流动对区域分布的影响。
-
未考虑人口年龄结构、城乡分布等结构性差异。
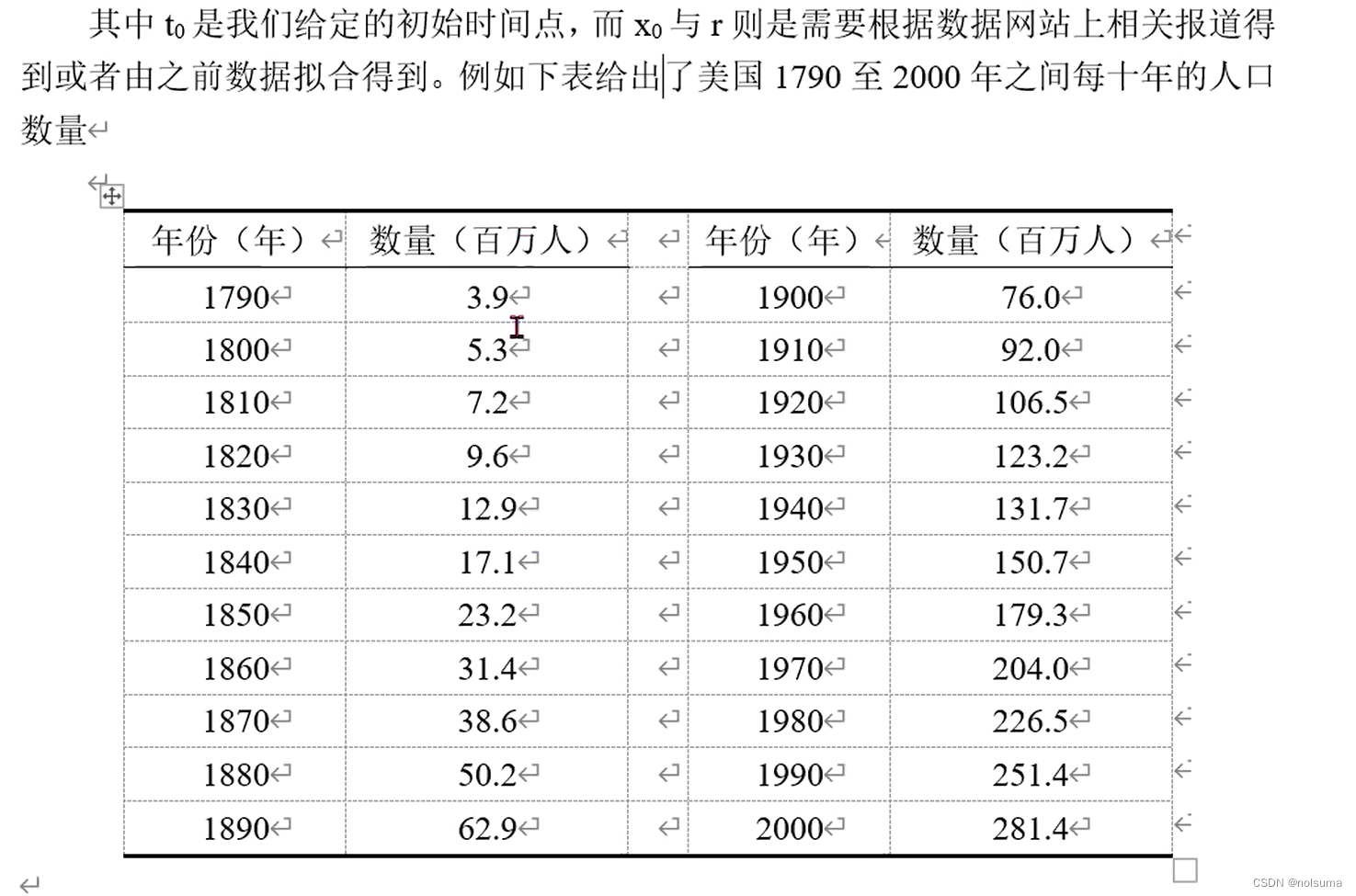
根据马尔萨斯人口增长模型,人口数量P与时间t的关系可表示为:
P0 - 初始人口数量
r - 人口增长率
e - 自然常数,约等于2.718
该式表示人口按照指数增长的关系随时间变化,即随着时间的推移,人口数量呈指数增长状态。
这个关系的主要特点有:
-
当t=0时,P(0)=P0,符合初始人口数量。
-
当t增大时,P随之快速增长。
-
增长率和初始人口数量会影响具体的增长速度。
-
在时间段内呈指数增长,不会出现饱和。
-
该关系反映了马尔萨斯模型的核心假设。
-
可以从数据中评估模型的参数P0和r。
-
可以用于短期人口增长预测。
matlab导入简单数据
year=1790:10:2000; population=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4]; p2=log(population); cftool
由于population人口数量P与时间t的关系不是线性的,所以令p2=log(population)使其变为线性。cftool是app中调用的曲线拟合工具。完成后,我们运行以上代码:
根据提供的代码和数据,使用MATLAB进行马尔萨斯模型的曲线拟合和分析的具体步骤如下:
(1)导入数据:点击“导入数据”,选择p2作为Y数据,year作为X数据。
(2)选择模型:选择“ exponent”指数形式。
(3)点击“拟合”按钮进行拟合。
在拟合类型中选择自定义方程:
r*(x-1790)+log(x0)
所以这个公式的意思是:
-
(x-1790)计算从初始年份到当前年份的时间跨度
-
r*(x-1790)计算这段时间内按增长率r的增长量
-
log(x0)代表初始人口数量对数
-
加起来则可以拟合整段时间内的人口数量对数
而后在拟合窗口得到结果:
常规模型:
f(x) = r*(x-1790)+log(x0)
系数(置信边界为 95%):
r = 0.02022 (0.01843, 0.02201)
x0 = 6.045 (4.718, 7.372)
拟合优度:
SSE: 1.304
R 方: 0.9652
调整 R 方: 0.9635
RMSE: 0.2553
所以得到人口预测函数方程:
% 完整过程:
% 定义年份和人口数据
year = 1790:10:2000;
population = [3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];
% 对数转换人口数据
p = log(population);
% 调用cftool进行曲线拟合
cftool(year,p)
% 在cftool中自定义方程
fittype('r*(x-1790)+log(x0)')
% 得到拟合方程
fit_eq = 'x=6.045*exp(0.02022*(t-1790))';
% 生成预测年份
year_pred = 1790:1:2020;
% 生成预测数据
population_pred = 6.045*exp(0.02022*(year_pred-1790));
% 绘制预测曲线
plot(year_pred,population_pred,'r-')
% 在同轴上绘制实际数据
hold on
plot(year,population,'bo')
% 修饰图表
legend('Predicted','Actual')
title('Population Prediction vs Actual')
xlabel('Year'); ylabel('Population')
hold off
可以预见的是,在人口增长后期,multhus模型不符合实际,需要引入新的模型限制其发展
Logistic阻滞增长模型
它揭示了一个普遍规律:缺乏约束的增长终会面临饱和状态。这启发我们复杂系统的思考。
- 反映资源约束条件下的增长规律
- 描述增长动力的衰减过程
- 模拟增长趋于稳定的规律
- 支持长期预测与规划
- 具有普适意义
r - 初始增长率,表示没有约束时的最大增长率。
s - 增长率衰减系数,控制增长率下降的速度。
x - 环境容量或资源量,代表外部约束条件。
r(x) - 在给定约束x下的增长率,随x变化而变化。
当x达到最大环境容纳量xm时,增长率r(xm)=0,将r(xm)=0带入原方程可得:r-sxm=0 --> sxm=r --> s=r/xm。
所以得到:
进一步的:
进一步的,增长率为:
*r(x)代表种群增长率,dx/dt 代表种群数量x随时间t变化的增长速度,dx/dt关联了决定因素r(x)和反馈因素x,描述增长动力衰减的机制。
转义为matlab的理解微分的方式:
x(t) - 表示种群数量随时间t的变化函数
xm - 表示种群最大容量,也就是增长的饱和值
x0 - 表示初始时间t0时的种群数量
r - 表示未受约束时的最大增长率
t - 表示时间
t0 - 表示增长的起始时间
MATLAB中实现logistic增长模型时,使用了较复杂的方程形式:
x(t) = xm / (1 + (xm/x0 - 1)exp(-r(t-t0)))
而不是更简单的微分方程表示:
dx/dt = r*(1 - x/xm)*x
这样实现的主要考虑如下:
-
微分方程dx/dt需要进行数值积分才能得到x(t),比较复杂。
-
而方程x(t)直接给出了解析解,可以直接带入t得到x。
-
对于给定参数,通过方程x(t)直接计算更简单快速。
-
MATLAB强大的符号计算能力,可以直接使用解析解。
-
使代码实现更简洁直接,不需要调用数值积分函数。
-
分析方程形式也有利于理解参数对曲线的影响。
-
微分方程更侧重本质关系,但解析解对计算更友好。
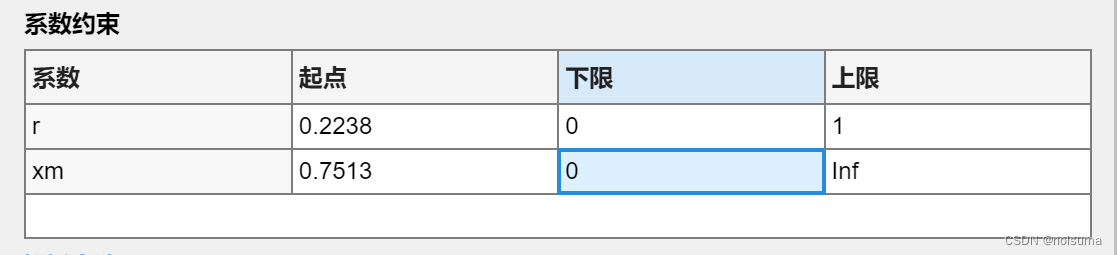
在进行拟合时,应该注意拟合系数约束
进行拟合分析时,需要将模型参数r和xm的下限约束为0的主要原因有:
-
r表示增长率,是非负值,若允许为负则失去实际意义。
-
xm表示种群最大容量,也必须是非负值。
-
如果不加约束,拟合可能得到r或xm为负的结果。
-
负的r或xm在实际情况下是不合理的。
-
加入非负约束可以避免得到不合理的拟合参数。
-
使拟合结果在实际意义上更可解释。
-
一般来说,加入参数约束条件可以提高拟合的质量。
-
反映问题背后的实际情况,获得更合理的模型。
-
也体现了建模过程中加入先验知识的思想。
最后得到拟合结果
常规模型:
f(x) = xm./(1+(xm./3.9-1).*exp(-r.*(x-1790)))
系数(置信边界为 95%):
r = 0.02735 (0.0265, 0.0282)
xm = 342.4 (311, 373.8)
拟合优度:
SSE: 1225
R 方: 0.9924
调整 R 方: 0.992
RMSE: 7.826
除此之外还有类似模型比如
Lotka-Volterra模型也称为竞争型种群模型,是生态学中一个典型的种群动力学模型。该模型主要描述两个互相竞争的种群(一般指捕食者和被捕食者)之间的动态关系。
Lotka-Volterra模型使用一对微分方程表示:
其中,
x表示被捕食者数量,y表示捕食者数量
a表示被捕食者繁殖率
b表示捕食率
c表示捕食者死亡率
d表示捕食效率
该模型反映了:
- 被捕食者自身增长受捕食影响
- 捕食者增长依赖被捕食者,但自身也面临死亡
- 两者互为制约因素,形成动态平衡
Lotka-Volterra模型揭示了族群间竞争对动态平衡的作用,在生态学及其他领域有重要应用价值。