差分进化算法(Differential Evolution,DE,附简单案例及详细matlab源码)
作者:非妃是公主
专栏:《智能优化算法》
博客地址:https://blog.csdn.net/myf_666
个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩
文章目录
- 专栏推荐
- 序
- 一、概论
- 二、差分进化算法(DE)原理
- 三、差分进化算法的优点
- 四、算法具体流程
- 1. 整体流程
- Ⅰ. 初始化
- Ⅱ. 变异
- Ⅲ. 交叉
- Ⅳ. 选择
- Ⅴ. 边界条件的处理
- 2. 细节处理
- Ⅰ. 种群数量 N P NP NP
- Ⅱ. 变异算子 F F F
- Ⅲ. 交叉算子 C R CR CR
- Ⅳ. 最大进化代数 G G G
- Ⅴ. 终止条件
- 五、仿真实例:差分进化求解函数最小值
- 1. 题目
- 2. 分析
- 3. matlab求解
- 4. 求解结果及分析
- 六、差分进化算法的一些改进方向
- 1. 自适应差分进化算法
- 2. 离散差分进化算法
- the end……
专栏推荐
专栏名称 专栏地址 软件工程 专栏——软件工程 计算机图形学 专栏——计算机图形学 操作系统 专栏——操作系统 软件测试 专栏——软件测试 机器学习 专栏——机器学习 数据库 专栏——数据库 算法 专栏——算法 序
在遗传、选择和变异的作用下,自然界生物体优胜劣汰,不断由低级向高级进化发展。人们注意到,适者生存的进化规律可以模式化,从而构成一些优化算法;近年来发展的进化计算类算法受到了广泛的关注。
一、概论
差分进化算法(Differential Evolution,DE)是一种新兴的进化计算技术。在1995年,由Storn等人提出用来解决切比雪夫多项式问题,后来发现它也是解决复杂优化问题的有效技术。
差分进化算法和遗传算法很相似,也是一种基于群体智能理论的优化算法,通过群体内个体间的合作与竞争而产生的全局搜索策略,采用实数编码、基于差分的简单变异操作和“一对一”的竞争生存策略,降低了进化计算操作的复杂性。
同时,差分进化算法具有记忆能力使其可以动态跟踪当前的搜索情况,以调整其搜索策略,具有较强的全局收敛能力和稳健性,且不需要借助问题的特征信息,适用于求解一些利用常规的数学规划方法很难求解,甚至无法求解的复杂优化问题。
二、差分进化算法(DE)原理
同其它进化算法一样(尤其和遗传算法,具有很强的相似性),差分进化算法,也是对候选解的种群进行操作,具体地说,它包含了三个主要的操作:
- 变异:通过把种群中两个成员之间的加权差向量加到第三个成员上来产生新的参数向量,该操作称为“变异”;
- 交叉:将变异向量的参数与另外预先确定的目标向量参数按照一定的规则混合来产生试验向量。
- 选择:如果试验向量的目标函数比目标向量的代价函数低,那么就利用试验向量替换掉目标向量。
种群中所有成成员必须要当作目标向量进行一次这样的操作,以便在下一代中出现相同个数的竞争者。在进化过程中,对每一代的向量都进行评价,记录最小化过程。
这种利用随机偏差扰动产生新个体的方式,可以获得一个收敛性非常好的结果,引导搜索过程向全局最优解逼近。
三、差分进化算法的优点
差分进化算法从提出到现在,短短二十几年的时间,取得了很多成功的应用。它具有以下优点:
- 结构简单,容易使用。一个是很容易实现,变异操作只涉及了向量的加减运算。再有就是算法的控制参数较少,这些参数对算法的性能影响已经有了一定的研究,可以供参考,因此,使用起来十分方便。
- 性能优越。差分进化算法具有较好的可靠性、高效性、鲁棒性。对于大空间、非线性和不可求导的连续问题,其求解速率比其他进化方法好,而且很多学者还在对差分进化算法继续改良,以不断提高其性能。
- 自适应性。差分变异算子可以根据不同的目标函数进行调整,从而提高搜索质量。
- 存在内在的并行性,可协同搜索。它具有利用个体局部信息和群体全局信息指导算法进一步搜索的能力。
- 算法通用,可直接对结构对象进行操作,不依赖于问题信息,不存在对目标函数的限定。比如许多问题是高维的,甚至是不可求导的,在这种情况下,使用差分进化算法就十分简单并不会增加求解的复杂性,而如果使用其它算法,很可能使得求解变得十分复杂。
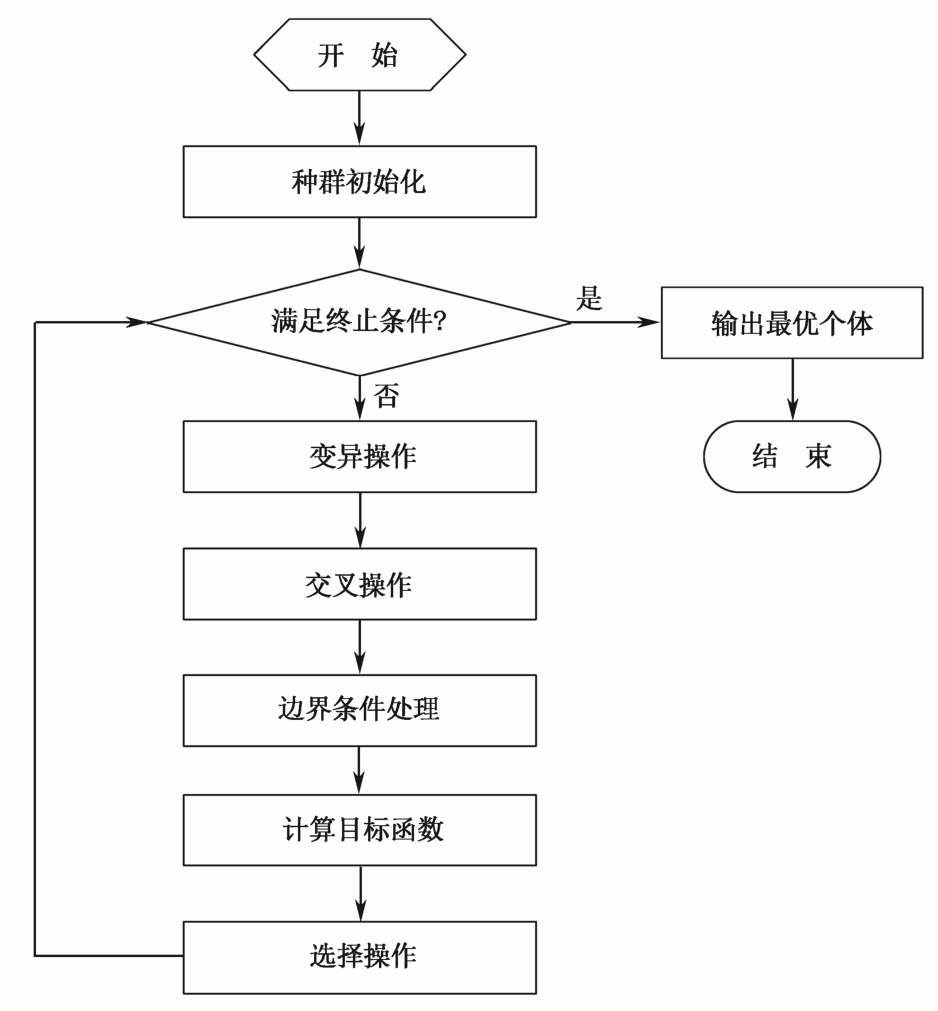
四、算法具体流程
学习的过程是广度优先,层层深入的,前面大致了解了差分进化算法的原理及思想,下面我们看一看差分进化算法的具体算法流程。
1. 整体流程
- 初始化;
- 变异;
- 交叉;
- 选择;
- 边界条件处理。
算法流程图如下:
Ⅰ. 初始化
初始化就是给种群中的每个个体的每个维度进行一个赋值,实现一个初始化的操作。每个个体表示如下:
x i , G ( i = 1 , 2 , . . . , N P ) x_{i,G}(i=1,2,...,NP) xi,G(i=1,2,...,NP)
其中, i i i 表示个体在种群中的编号, G G G 表示进化代数, N P NP NP 代表种群规模。
在差分进化算法中,一般假定所有随机初始化种群均符合均匀分布。设参数变量的界限为 x j ( L )