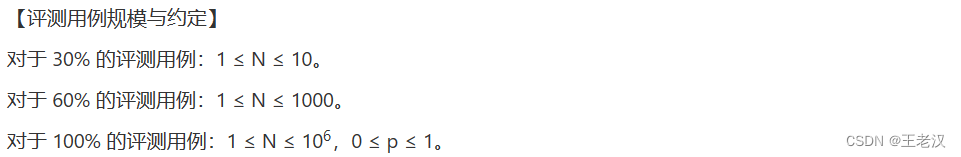2024年十五届蓝桥杯省赛大学B组真题(Java完整版)
2024年十五届蓝桥杯省赛大学B组真题(Java)
前言:
赛后一直犹豫要不要对比赛进行复盘出个题解,拖到了现在,终于也是等到比赛结果出来,看到没有辜负个人期望成功取得省一,决定在国赛前对省赛进行一个复盘,顺带查漏补缺,总体而言,这次JavaB组的省赛题偏基础,没有太多的算法,也是延续了暴力杯的头衔,这次对数学的考察居然比以往提高了不少,令我感到意外,题外话不多说,让我们一起来复盘一下第十五届的省赛题吧,同时也祝愿各位能取得一个不错的成绩。
(未完篇)
题单链接
点击此处跳转
试题A:报数游戏
本题总分:5 分
【问题描述】
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:2429042904288
【解题思路】
该题数据量大,单纯靠电脑跑不太现实,那么其中肯定有数学规律在,通过计算可以得出 20 和 24 的最小公倍数是 120 ,再对符合条件的前四十个数进行输出,我们可以发现该规律是十次一循环,每次结尾都是 120 的倍数,那么我们可以求得第 202420242020 个数的值为 202420242020/10*120=2429042904240 ,再通过观察发现第四个数与上一个循环相差 48 ,把两个数值相加得到答案 2429042904288
【代码】
package SS2024b.baoshuyouxi;
public class Main {
public static void main(String[] args) {
long n = 202420242024L;
// long count = 0;
// for (long i = 1; count
试题 B: 类斐波那契循环数
本题总分:5 分
【问题描述】
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:7913837
【解题思路】
给出一个判断是否为类斐波那契循环数的判断式,该判断式类似于滚动窗口,固定取一个窗口大小,该大小为 n 的值,维护窗口内所有值的和 sum ,判断 sum 在小于等于 n 是是否存在相等的情况即可,从 1e7 开始一直递减遍历下去,遇到的第一个符合条件的数即为答案。
【代码】
package SS2024b.leifeibonaqixunhuan;
import java.util.ArrayList;
public class Main {
public static void main(String[] args) {
int l = (int) 1e7;
while (l > 0) {
if (isLei(l)) {
System.out.println(l);
break;
}
l--;
}
}
static boolean isLei(int n) {
boolean flag = false;
int n1 = n;
ArrayList ys = new ArrayList();
while (n1 != 0) {
ys.add(n1 % 10);
n1 /= 10;
}
ArrayList s = new ArrayList();
s.add(0);
int sum = 0;
for (int i = ys.size() - 1; i >= 0; i--) {
s.add(ys.get(i));
sum += ys.get(i);
}
int index = 0;
while (sum
if (index != 0) {
sum *= 2;
}
s.add(sum -= s.get(index++));
if (sum == n) {
flag = true;
break;
}
}
return flag;
}
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
ArrayList
list[i] = new ArrayList
String cz = scan.next();
if (cz.equals("add")) {
int element = scan.nextInt();
list[0].add(element);
} else if (cz.equals("sync")) {
int follower_id = scan.nextInt();
if (list[0].size() != list[follower_id].size()) {
list[follower_id].add(list[0].get(list[follower_id].size()));
}
} else if (cz.equals("query")) {
int min = list[0].size();
for (int i = 1; i
试题 E: 最优分组
时间限制: 3.0s 内存限制: 512.0MB 本题总分:15 分
【问题描述】
【输入格式】
第一行,一个整数 N。
第二行,一个浮点数 p。
【输出格式】
输出一行,一个整数 K 表示答案。
【样例输入】
1000
0.05
【样例输出】
5
【样例说明】
无
【评测用例规模与约定】
【解题思路】
本题是求解数学期望值,最大期望用试剂量为 N ,分成每组 k 只宠物后,生病概率为 1-(1-p)
k
^k
k ,固定要使用的试剂量为 n/k ,如果一组宠物生病的额外用试剂量为 k ,生病的总用试剂量为 k*[1-(1-p)
k
^k
k]n/k ,则总的期望用试剂量为 k[1-(1-p)
k
^k
k]*n/k+n/k 利用该式可求得最小期望值所代表的 k 。
【代码】
package SS2024b.zuiyoufenzu;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
double p = scan.nextDouble();
double min = 1.0 * n;
int min_index = 1;
for (int k = 1; k
if (n % k == 0) {
double num = k * (1 - Math.pow(1 - p, k)) * n / k + n / k;
if (num