第十三届蓝桥杯大赛软件赛省赛(Python大学A组)
2022年蓝桥杯 省赛真题
Python大学A组
试题A:裁纸刀
试题B:寻找整数
试题C:质因数个数
试题D:矩形拼接
试题E:消除游戏
试题F:重新排序
试题G:全排列的价值
试题H:最长不下降子序列
试题I:最优清零方案
试题J:数的拆分
试题A:裁纸刀 (5分)
【问题描述】
小蓝有一个裁纸刀,每次可以将一张纸沿一条直线裁成两半,小蓝用一张纸打印出两行三列共6个二维码,至少使用九次裁出来,下图给出了一种裁法。
在上面的例子中,小蓝的打印机没办法打印到边缘,所以边缘至少要裁4次。另外,小蓝每次只能裁一张纸,不能重季或者拼起来裁。如果小蓝要用一张纸打印出20行22列共440个二维码,他至少需要裁多少次?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只输出这个整数,输出多余的内容将无法得分。
【解析与方法】
一道简单的数学题 先看例子,边缘必须裁四次,然后得到两行三列共六张二维码。 横线5裁一次,竖线6 7 8 9各裁一次,加上裁边缘的四次,共九次。 也就是说,横向裁剪次数为【行数-1】次。 竖向裁剪次数为【(列数-1)*行数】次。 题目共20行22列,则次数为:4 + 19 + (21*20) = 443次。可以证明这种方法是裁剪次数最少的方法。所以当行数为20行、列数为22列的440个二维码最少需要:(20-1) + (22-1)*20 + 4 = 443
【Python程序代码】
print(20-1 + (22-1)*20 + 4)
最终结果:443
试题B:寻找整数 (5分)
【问题描述】
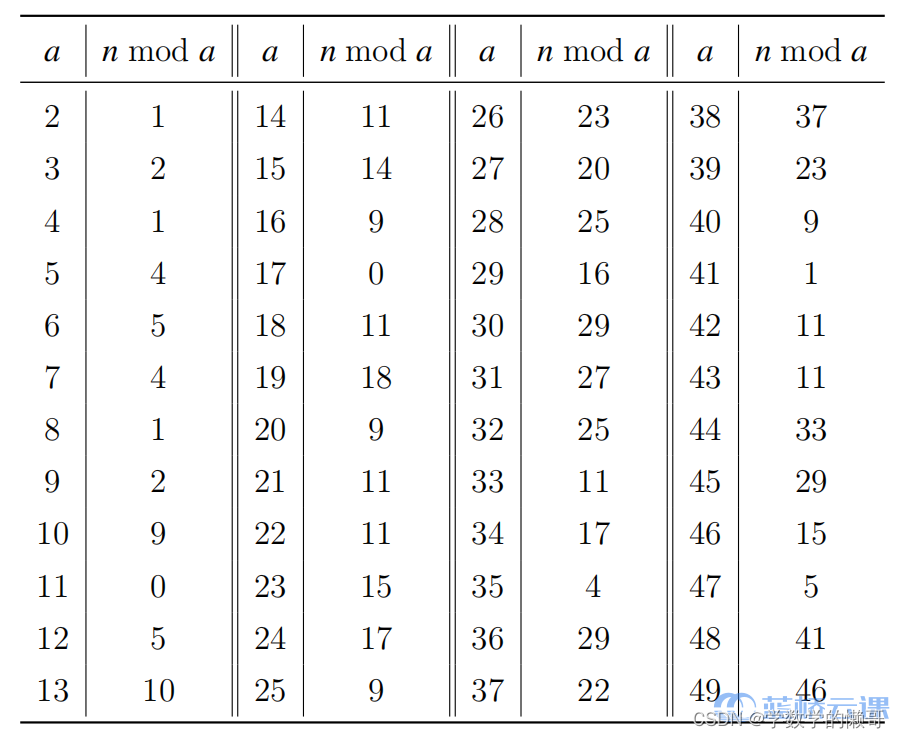
有一个不超过10的17次方的正整数n,知道这个数除以2至49后的余数如下表所示,求这个正整数最小是多少?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只输出这个整数,输出多余的内容将无法得分。
【解析与方法】
首先比较明显可以看出这应该属于线性同余方程组求解的问题,题目已经表明有解,所以可以直接采用中国剩余定理来求解。
首先明确所以的质数2~49的质数ai,以及对于的余数mi.
可以等价于:
存在通解:
令通解最小且符合条件:
带入第一个式子得:
即可以令m1 = a1k1+m1,a1 = k(a1a2)/d,继续迭代得到最终结果。
【Python程序代码】
import math
a = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47]
m = [1,2,4,4,0,10,0,18,15,16,27,22,1,11,5]
a1,m1 = a[0],m[0]
def extended_gcd(a, b):
if b == 0:
return a, 1, 0
else:
gcd, x, y = extended_gcd(b, a % b)
return gcd, y, x - (a // b) * y
def mod(a,b):
return ((a%b)+b)%b
for i in range(1,len(a)):
d,k1,k2 = extended_gcd(a1,a[i])
k1 = mod(k1*(m[i]-m1)//d,int(math.fabs(a[i]/d)))
m1 = k1*a1 + m1
a1 = int(math.fabs(a1//d*a[i]))
print(m1)
最终结果:2022040920220409
试题C:质因数个数 (10分)
【题目描述】
给定正整数n,请问有多少个质数是n的约数?
【输入格式】
输入的第一行包含一个整数n。
【输出格式】
输出一个整数,表示n的质数约数个数。
【样例输入】
396
【样例输出】
3
【测评用例与规模】
对于30%的评测用例,1