深度解析：数据结构二叉树（1）

✅作者简介：大家好，我是再无B～U～G，一个想要与大家共同进步的男人😉😉 🍎个人主页： 再无B～U～G-CSDN博客 目标 1. 掌握树的基本概念 2. 掌握二叉树概念及特性 3. 掌握二叉树的基本操作

1. 树型结构

1.1 概念

树是一种 非线性 的数据结构，它是由 n （ n>=0 ）个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看 起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的 。它具有以下的特点：

1. 有一个特殊的结点，称为根结点，根结点没有前驱结点
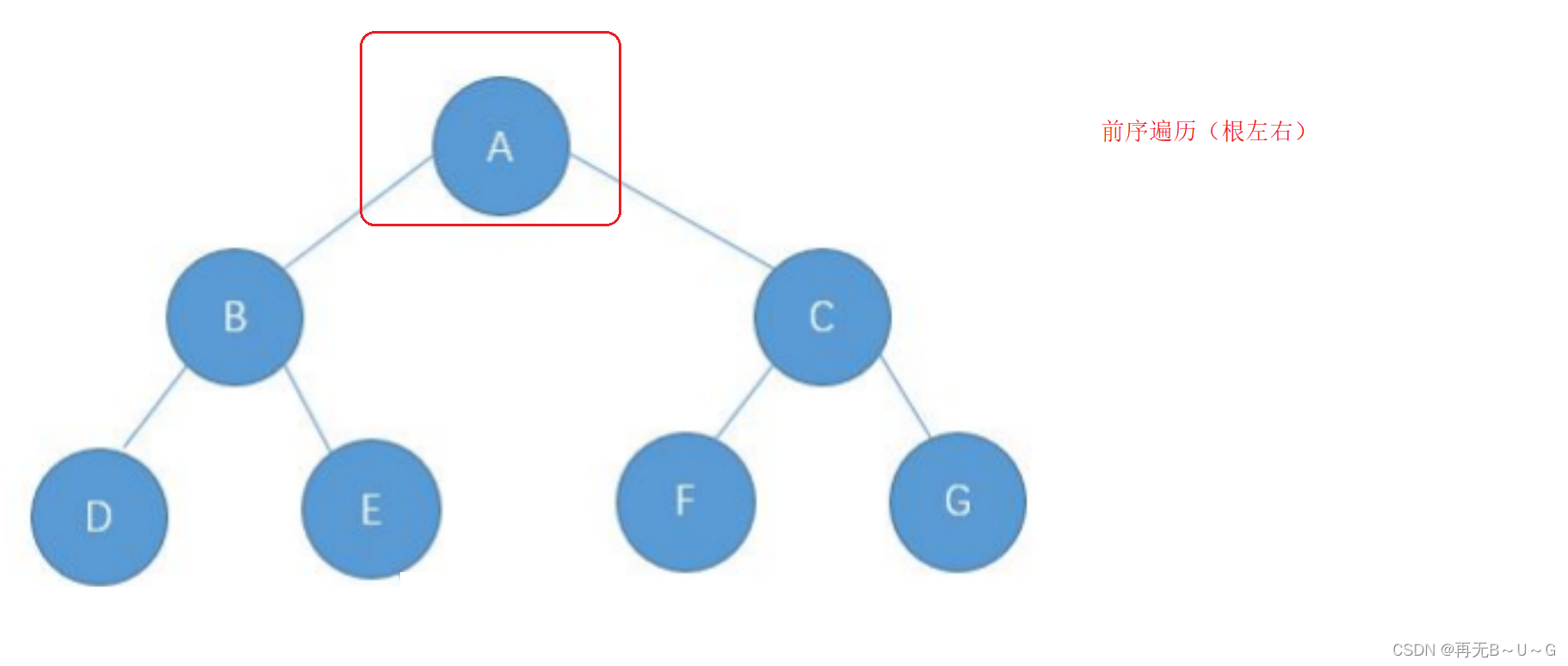
2. 除根结点外，其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm，其中每一个集合Ti (1 根的左子树 ---> 根的右子树。 （根左右） LNR ：中序遍历 (Inorder Traversal)—— 根的左子树 ---> 根节点 --->根的右子树。 （左根右） LRN ：后序遍历 (Postorder Traversal)—— 根的左子树 ---> 根的右子树 --->根节点。 （左右根）

    // 前序遍历

   void preOrder ( Node root ); // 中序遍历 void inOrder ( Node root ); // 后序遍历 void postOrder ( Node root )

    下面主要分析前序递归遍历，中序与后序图解类似，同学们可自己动手绘制。

   

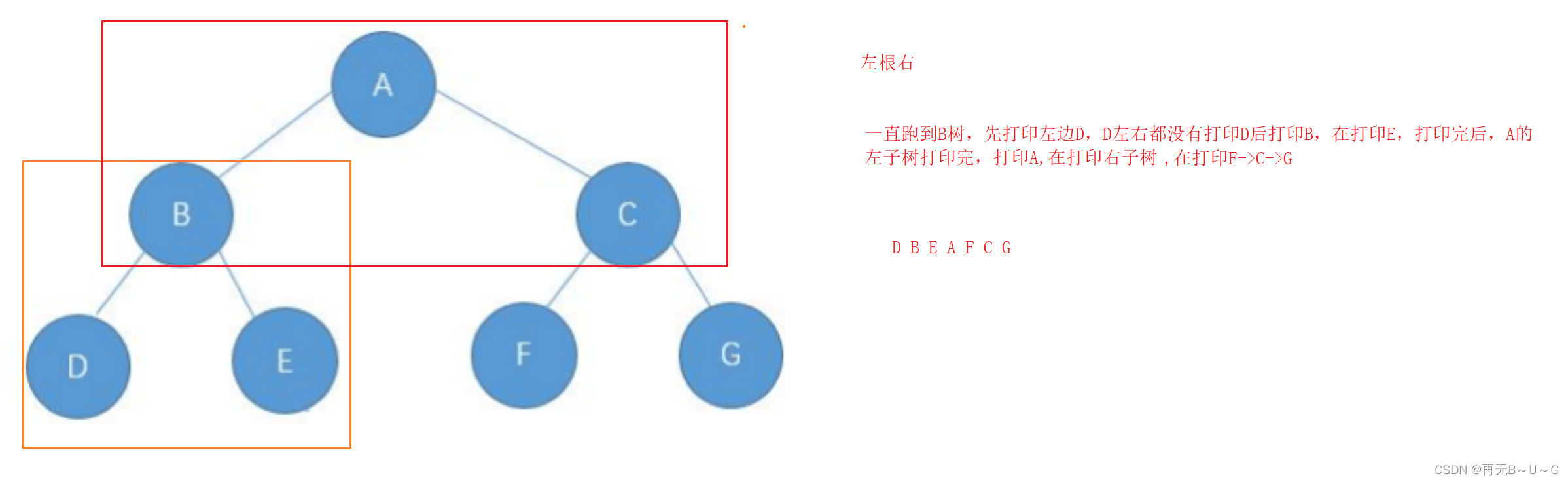
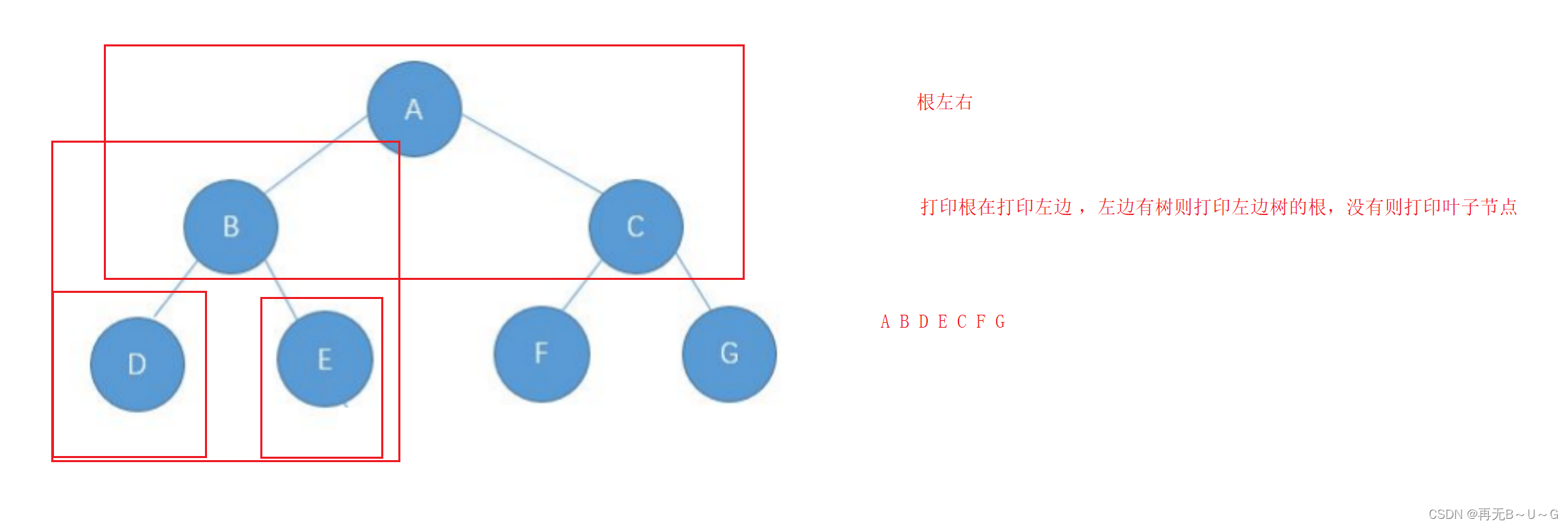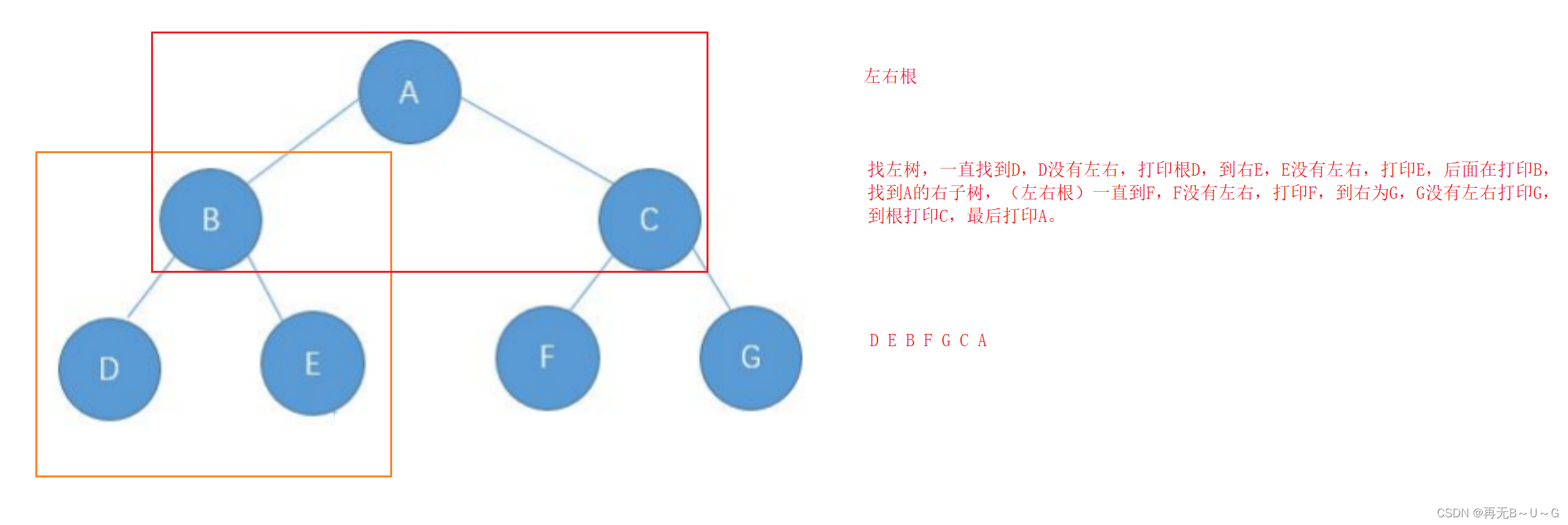
   前序遍历结果：ABCDEFG 分析： 中序遍历结果：DBEAFCG 后序遍历结果：DEBFGCA

    

   选择题 

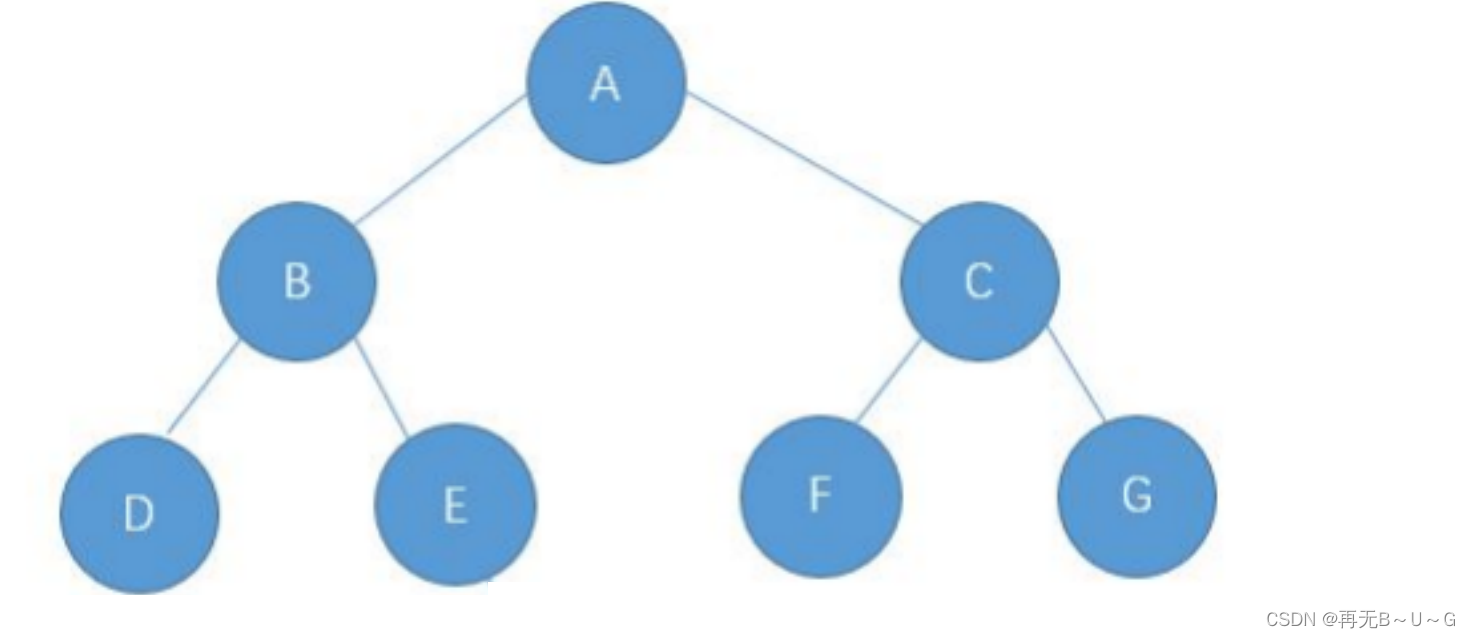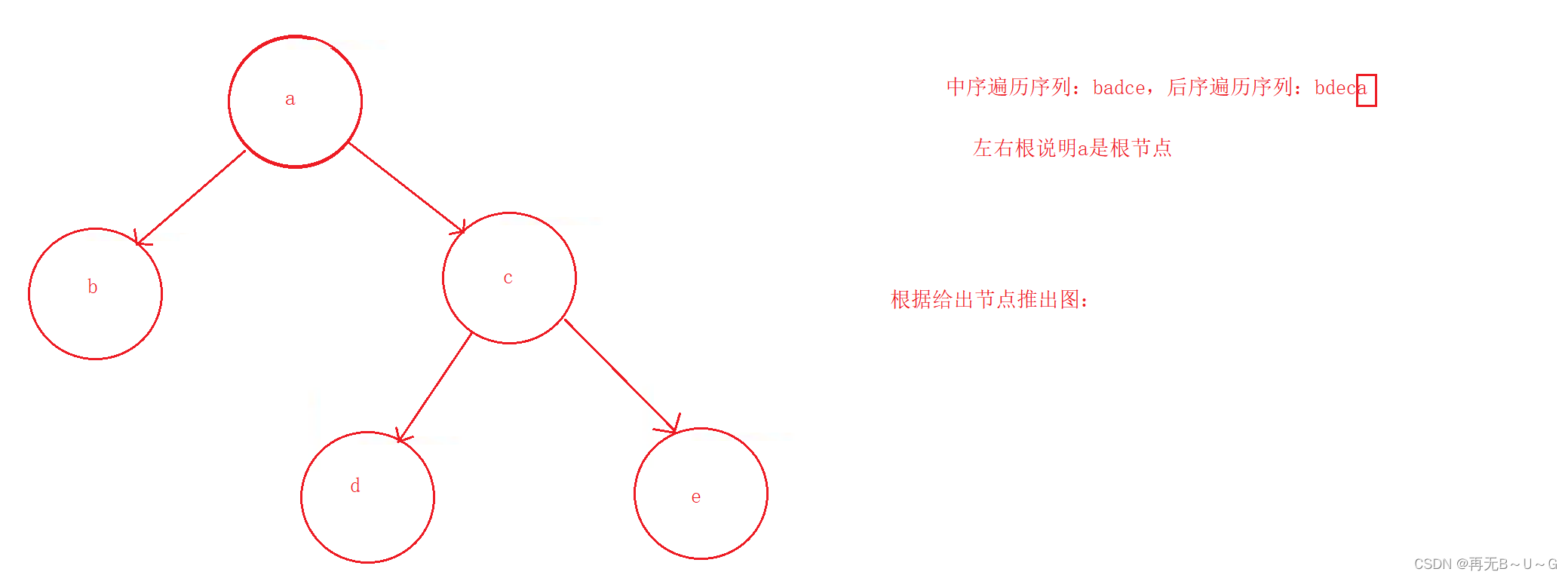
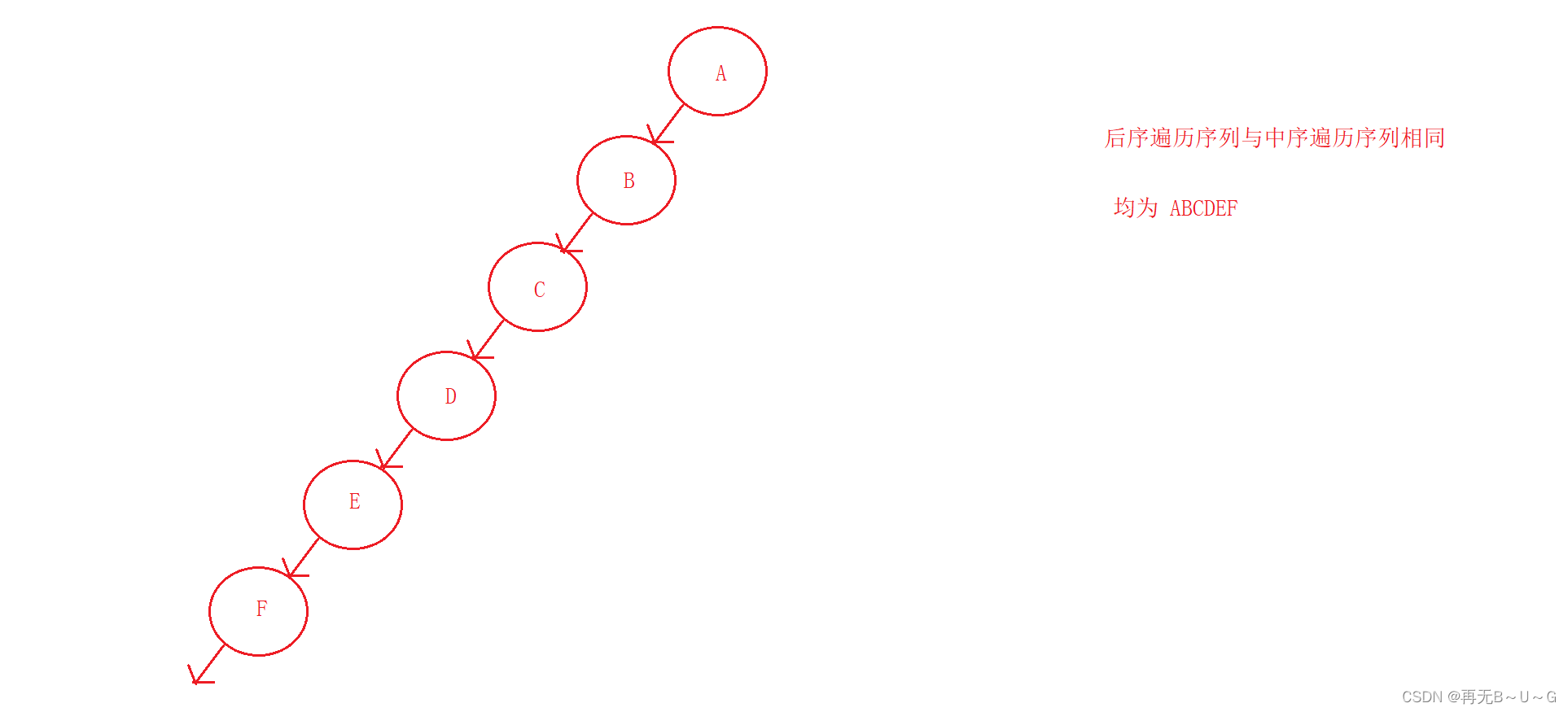
   1. 某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为 () A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA 2. 二叉树的先序遍历和中序遍历如下：先序遍历： EFHIGJK; 中序遍历： HFIEJKG. 则二叉树根结点为 () A: E B: F C: G D: H 3. 设一课二叉树的中序遍历序列： badce ，后序遍历序列： bdeca ，则二叉树前序遍历序列为 () A: adbce B: decab C: debac D: abcde 4. 某二叉树的 后序遍历序列与中序遍历序列相同 ，均为 ABCDEF ，则按层次输出 ( 同一层从左到右 ) 的序列为 () A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF 【参考答案】 1.A 2.A 3.D 4.A

   前序遍历代码：

       //前序遍历
       void preOrder(BTNode root) {
           if (root == null) {
               return;
           }
           System.out.print(root.ch + " ");
           //递归遍历左子树
           preOrder(root.left);
           //递归遍历右子树
           preOrder(root.right);
       }

   中序遍历代码：

     //中序遍历
       void inOrder(BTNode root) {
           if (root == null) {
               return;
           }
           //递归遍历左子树
           inOrder(root.left);
           System.out.print(root.ch + " ");
           //递归遍历右子树
           inOrder(root.right);
       }

   后序遍历代码：

       //后序遍历
       void postOrder(BTNode root){
           if(root == null){
               return;
           }
           //递归遍历左子树
           postOrder(root.left);
           //递归遍历右子树
           postOrder(root.right);
           System.out.print(root.ch + " ");
       }

    2.5.3 二叉树的基本操作

       // 获取树中节点的个数
       int size(BTNode root){
           if(root == null){
               return 0;
           }
           //递归遍历左子树
           //递归遍历右子树
           int ret = size(root.left) + size(root.right) + 1;
           return ret;
       }
       // 获取叶子节点的个数
       int getLeafNodeCount(BTNode root){
           if(root == null){
               return 0;
           }
           if(root.left == null && root.right == null){
               return 1;
           }
           return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);
       }
       // 子问题思路-求叶子结点个数
       // 获取第K层节点的个数
       int getKLevelNodeCount(BTNode root,int k){
           if(root == null) {
               return 0;
           }
           if(k == 1) {
               return 1;
           }
           return getKLevelNodeCount(root.left,k-1) +
                   getKLevelNodeCount(root.right,k-1);
       }
       // 获取二叉树的高度
       int getHeight(BTNode root){
           if(root == null) {
               return 0;
           }
           int leftHeight = getHeight(root.left);
           int rightHeight = getHeight(root.right);
           return leftHeight > rightHeight ?
                   leftHeight+1:rightHeight+1;
       }
       // 检测值为value的元素是否存在
       BTNode find(BTNode root,char val){
           if(root == null) {
               return null;
           }
           if(root.ch == val) {
               return root;
           }
           //左边找
           BTNode ret = find(root.left,val);
           if(ret != null) {
               return ret;
           }
           //右边找
           ret = find(root.right,val);
           if(ret != null) {
               return ret;
           }
           return null;
       }
       //层序遍历
       void levelOrder(BTNode root){
           //双向列表当列队
           Queue queue = new LinkedList();
           if(root == null) {
               return;
           }
           queue.offer(root);
           while (!queue.isEmpty()) {
               BTNode cur = queue.poll();
               System.out.print(cur.ch+" ");
               if(cur.left != null) {
                   queue.offer(cur.left);
               }
               if(cur.right != null) {
                   queue.offer(cur.right);
               }
           }
           System.out.println();
       }
       // 判断一棵树是不是完全二叉树
       boolean isCompleteTree(BTNode root){
           Queue queue = new LinkedList();
           if(root == null) return true;
           queue.offer(root);
           while (!queue.isEmpty()) {
               BTNode cur = queue.poll();
               if(cur == null) {
                   break;
               }
               queue.offer(cur.left);
               queue.offer(cur.right);
           }
           while (!queue.isEmpty()) {
               BTNode node = queue.peek();
               if(node != null) {
                   return false;
               }else {
                   queue.poll();
               }
           }
           return true;
       }

   好了，今天就到这里了，感谢观看。