matlab（实例）：滤波器（低通、带通、高通，使用butter函数、filter函数）

05-09 1334阅读

一、题目：已知一个时域信号，包含三个频率（50Hz、150Hz、300Hz），分别设计并使用低通滤波器、带通滤波器、高通滤波器，对其进行滤波，画出滤波信号的时域图和频谱图。

$matlab（实例）：滤波器（低通、带通、高通，使用butter函数、filter函数）$

二、解题过程：

①函数介绍：

本次编码使用函数butter函数和filter函数

1、butter()

用于计算滤波器系数

语法：

[b,a] = butter(n,Wn)

[b,a] = butter(n,Wn,ftype)

[z,p,k] = butter(___)

[A,B,C,D] = butter(___)

[___] = butter(___,'s')

输入参数

n - 滤波器阶数

整数标量

Wn - 截止频率，注意：Wn = fc_low/(fs/2)

标量 | 二元素向量

ftype - 滤波器类型

'low' | 'bandpass' | 'high' | 'stop'

输出参数

b,a - 传递函数系数

行向量

z,p,k - 零点、极点和增益

列向量、标量

A,B,C,D - 状态空间矩阵

矩阵

2、filter()

使用滤波器对信号进行滤波

语法

y = filter(b,a,x)

y = filter(b,a,x,zi)

y = filter(b,a,x,zi,dim)

[y,zf] = filter(___)

输入参数

b - 有理传递函数的分子系数

向量

a - 有理传递函数的分母系数

向量

x - 输入数据

向量 | 矩阵 | 多维数组

zi - 滤波器延迟的初始条件

[] (默认值) | 向量 | 矩阵 | 多维数组

dim - 沿其运算的维度

正整数标量

输出参数

y - 滤波后的数据

向量 | 矩阵 | 多维数组

zf - 滤波器延迟的最终条件

向量 | 矩阵 | 多维数组

②代码

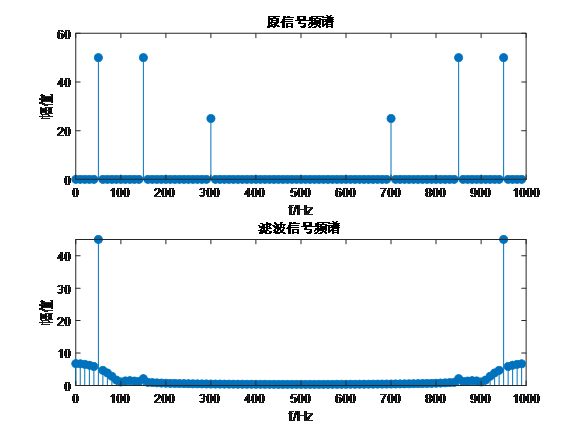
1、低通滤波器

clc 
clear
close all
% 创建一个测试信号
fs = 1000; % 采样频率
t = 0:1/fs:1; % 时间向量
x = sin(2*pi*50*t) + sin(2*pi*150*t) + 0.5*sin(2*pi*300*t); % 包含50Hz、150Hz和300Hz成分的信号
fc_low = 100; % 低截止频率
fc_high = 200; % 高截止频率
N = 7; % 滤波器阶数
[b, a] = butter(N, fc_low/(fs/2), 'low'); % 计算低通滤波器系数
% [b, a] = butter(N, [fc_low/(fs/2), fc_high/(fs/2)], 'bandpass'); % 计算中通滤波器系数
% [b, a] = butter(N, fc_high/(fs/2), 'high'); % 计算中高通滤波器系数
% 使用中通滤波器对信号进行滤波
y = filter(b, a, x);
% 绘制原始信号和滤波后的信号
figure;
subplot(2,1,1);
plot(t, x);
title('原始信号');
xlabel('t/s');
ylabel('幅值');
subplot(2,1,2);
plot(t, y);
title('滤波信号');
xlabel('t/s');
ylabel('幅值');
% 傅里叶变换，画频谱图
Ns = 100; % 傅里叶变换采样点数
delta_f = fs/Ns; % 频率分辨率
x_f = (0:Ns-1)*delta_f; % 频域信号横轴
S_f = fft(x(1:Ns));
figure(2)
subplot(2,1,1)
stem(x_f, abs(S_f), 'filled');
title('原信号频谱')
xlabel('f/Hz')
ylabel('幅值')
y_f = (0:Ns-1)*delta_f; % 频域信号横轴
Y_f = fft(y(1:Ns));
subplot(2,1,2)
stem(y_f, abs(Y_f), 'filled');
title('滤波信号频谱')
xlabel('f/Hz')
ylabel('幅值')

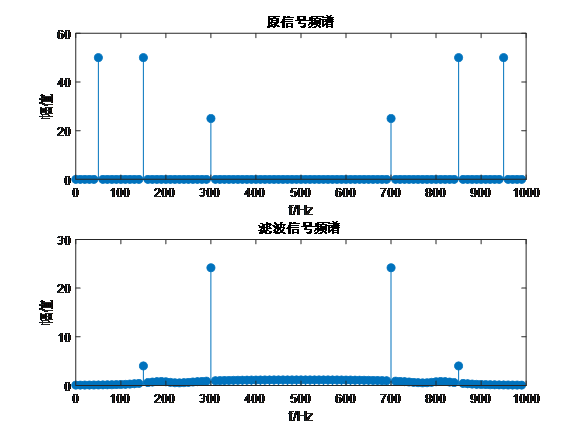
2、带通滤波器

clc 
clear
close all
% 创建一个测试信号
fs = 1000; % 采样频率
t = 0:1/fs:1; % 时间向量
x = sin(2*pi*50*t) + sin(2*pi*150*t) + 0.5*sin(2*pi*300*t); % 包含50Hz、150Hz和300Hz成分的信号
fc_low = 100; % 低截止频率
fc_high = 200; % 高截止频率
N = 7; % 滤波器阶数
% [b, a] = butter(N, fc_low/(fs/2), 'low'); % 计算低通滤波器系数
[b, a] = butter(N, [fc_low/(fs/2), fc_high/(fs/2)], 'bandpass'); % 计算中通滤波器系数
% [b, a] = butter(N, fc_high/(fs/2), 'high'); % 计算中高通滤波器系数
% 使用中通滤波器对信号进行滤波
y = filter(b, a, x);
% 绘制原始信号和滤波后的信号
figure;
subplot(2,1,1);
plot(t, x);
title('原始信号');
xlabel('t/s');
ylabel('幅值');
subplot(2,1,2);
plot(t, y);
title('滤波信号');
xlabel('t/s');
ylabel('幅值');
% 傅里叶变换，画频谱图
Ns = 100; % 傅里叶变换采样点数
delta_f = fs/Ns; % 频率分辨率
x_f = (0:Ns-1)*delta_f; % 频域信号横轴
S_f = fft(x(1:Ns));
figure(2)
subplot(2,1,1)
stem(x_f, abs(S_f), 'filled');
title('原信号频谱')
xlabel('f/Hz')
ylabel('幅值')
y_f = (0:Ns-1)*delta_f; % 频域信号横轴
Y_f = fft(y(1:Ns));
subplot(2,1,2)
stem(y_f, abs(Y_f), 'filled');
title('滤波信号频谱')
xlabel('f/Hz')
ylabel('幅值')

3、高通滤波器

clc 
clear
close all
% 创建一个测试信号
fs = 1000; % 采样频率
t = 0:1/fs:1; % 时间向量
x = sin(2*pi*50*t) + sin(2*pi*150*t) + 0.5*sin(2*pi*300*t); % 包含50Hz、150Hz和300Hz成分的信号
fc_low = 100; % 低截止频率
fc_high = 200; % 高截止频率
N = 7; % 滤波器阶数
% [b, a] = butter(N, fc_low/(fs/2), 'low'); % 计算低通滤波器系数
% [b, a] = butter(N, [fc_low/(fs/2), fc_high/(fs/2)], 'bandpass'); % 计算中通滤波器系数
[b, a] = butter(N, fc_high/(fs/2), 'high'); % 计算中高通滤波器系数
% 使用中通滤波器对信号进行滤波
y = filter(b, a, x);
% 绘制原始信号和滤波后的信号
figure;
subplot(2,1,1);
plot(t, x);
title('原始信号');
xlabel('t/s');
ylabel('幅值');
subplot(2,1,2);
plot(t, y);
title('滤波信号');
xlabel('t/s');
ylabel('幅值');
% 傅里叶变换，画频谱图
Ns = 100; % 傅里叶变换采样点数
delta_f = fs/Ns; % 频率分辨率
x_f = (0:Ns-1)*delta_f; % 频域信号横轴
S_f = fft(x(1:Ns));
figure(2)
subplot(2,1,1)
stem(x_f, abs(S_f), 'filled');
title('原信号频谱')
xlabel('f/Hz')
ylabel('幅值')
y_f = (0:Ns-1)*delta_f; % 频域信号横轴
Y_f = fft(y(1:Ns));
subplot(2,1,2)
stem(y_f, abs(Y_f), 'filled');
title('滤波信号频谱')
xlabel('f/Hz')
ylabel('幅值')