常见的激活函数(sigmoid、tanh、ReLU、Leaky ReLU、P-ReLU、R-ReLU、ELU、Swish、Mish、Maxout、softmax)
文章目录
- 前言
- 求导四则运算法则
- 基本初等函数的导数
- sigmoid函数
- sigmoid函数适用场景
- sigmoid函数图像
- sigmoid函数的导数公式
- sigmoid函数的导数图像
- sigmoid函数的缺点
- 解决办法
- tanh函数
- tanh函数公式推导过程
- tanh函数图像
- tanh函数的导数公式
- tanh函数的导数图像
- t a n h ( x ) + 1 = 2 s i g m o i d ( 2 x ) tanh(x) + 1 = 2sigmoid(2x) tanh(x)+1=2sigmoid(2x)
- sigmoid和tanh函数图像对比
- ReLU函数
- ReLU函数图像
- ReLU在零点处不可导
- ReLU函数负半区间也是非线性激活函数的理解
- 使用ReLU的原因
- ReLU6
- Leaky ReLU函数
- Leaky ReLU函数优缺点
- 优点
- 缺点
- 参数化ReLU(P-ReLU)
- 随机化ReLU(R-ReLU)
- 指数化线性单元(ELU)
- 软饱和性和无饱和性
- ELU指数线性单元特点
- 缺点
- Swish函数
- SiLU
- Mish函数
- Maxout函数
- softmax函数
- softmax函数公式
- softmax函数的导数公式
- 当 i ≠ j i ≠ j i=j 时
- 当 i = j i = j i=j 时
- softmax溢出问题
- 参考文章
- 上溢出(overflow)和下溢出(underflow)
- 解决方法
- 延伸问题
- 解决方法
- softmax函数在多分类问题中的应用
- 激活函数的应用场景
前言
本文首先回回顾了求导四则运算法则和常见基本初等函数的导数,目的是为了对下文激活函数公式的推导做铺垫。接着介绍了sigmoid函数,并提出了sigmoid函数存在的期望不为0且梯度消失问题。因此,基于sigmoid函数的缺陷提出了tanh(x)激活函数。虽然tanh函数在一定程度上缓解了sigmoid函数带来的“均值不为0”的问题,但是仍然存在“梯度饱和”的现象。为了避免梯度饱和现象的发生,修正线性单元(Rectified Linear Unit, ReLU)被提出。但是ReLU存在“死区”现象。为了缓解死区现象,研究者们提出了一些ReLU的变种,如Leaky ReLU、Parametric ReLU(PReLU)、Exponential Linear Unit(ELU)等。另外,本文详细地推导了softmax函数的导数公式和探讨了softmax溢出问题,并给出了解决方案。最后,提及了一些常用激活函数的应用场景。
求导四则运算法则
若函数 u ( x ) {u(x)} u(x), v ( x ) {v(x)} v(x) 都可导,则
( u ( x ) ± v ( x ) ) ′ = u ′ ( x ) ± v ′ ( x ) ( u ( x ) ∙ v ( x ) ) ′ = u ′ ( x ) ∙ v ( x ) + u ( x ) ∙ v ′ ( x ) ( u ( x ) v ( x ) ) ′ = u ′ ( x ) v ( x ) − v ′ ( x ) u ( x ) v 2 ( x ) \begin{gathered}\left(u\left(x\right)\pm v\left(x\right)\right)^{^{\prime}}=u^{^{\prime}}\left(x\right)\pm v^{^{\prime}}\left(x\right)\\\left(u\left(x\right)\bullet v\left(x\right)\right)^{^{\prime}}=u^{^{\prime}}\left(x\right)\bullet v\left(x\right)+u\left(x\right)\bullet v^{^{\prime}}\left(x\right)\\\left(\frac{u\left(x\right)}{v\left(x\right)}\right)^{^{\prime}}=\frac{u^{^{\prime}}\left(x\right)v\left(x\right)-v^{^{\prime}}\left(x\right)u\left(x\right)}{v^{2}\left(x\right)}\end{gathered} (u(x)±v(x))′=u′(x)±v′(x)(u(x)∙v(x))′=u′(x)∙v(x)+u(x)∙v′(x)(v(x)u(x))′=v2(x)u′(x)v(x)−v′(x)u(x)
基本初等函数的导数
sigmoid函数
sigmoid函数也叫Logistic函数,对于一个定义域在 R {R} R中的输入,sigmoid函数将输入变换为区间(0,1)上的输出。因此,sigmoid通常称为挤压函数(squashingfunction):它将范围(‐inf,inf)中的任意输入压缩到区间(0,1)中的某个值:
s i g m o i d ( x ) = 1 1 + exp ( − x ) sigmoid(x)=\frac{1}{1+\exp (-x)} sigmoid(x)=1+exp(−x)1
sigmoid函数适用场景
当我们想要将输出视作二元分类问题的概率时,sigmoid仍然被广泛用作输出单元上的激活函数(sigmoid可以视为softmax的特例)。然而,sigmoid在隐藏层中已经较少使用,它在大部分时候被更简单、更容易训练的ReLU所取代。
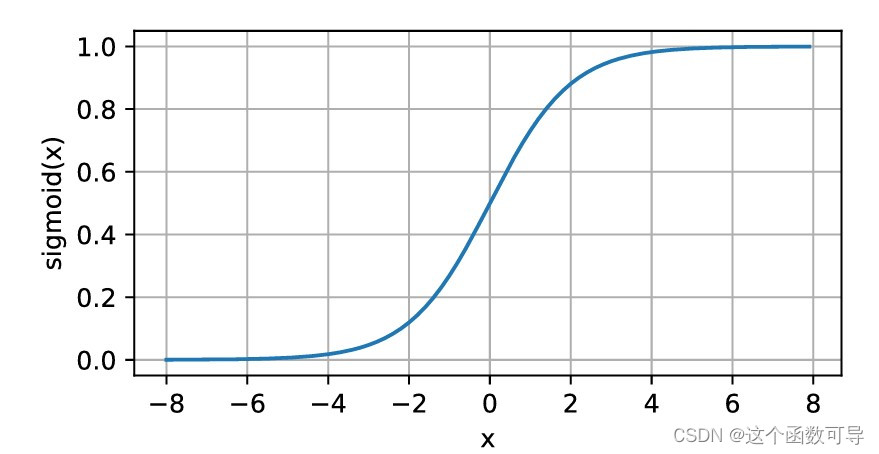
sigmoid函数图像
下面,我们绘制sigmoid函数。注意,当输入接近0时,sigmoid函数接近线性变换。
从上图可以看出,sigmoid函数的性质如下:
- 关于 ( 0 , 0.5 ) (0,0.5) (0,0.5)中心对称,其值全部大于0
- sigmoid可以将实数域的值映射到 ( 0 , 1 ) (0,1) (0,1)之间,赋予了概率的意义
- 在sigmoid函数值
x
>
5
x>5
x>5或者
x
使用ReLU的原因
使用ReLU的原因是,它求导表现得特别好:要么让参数消失,要么让参数通过。这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题。
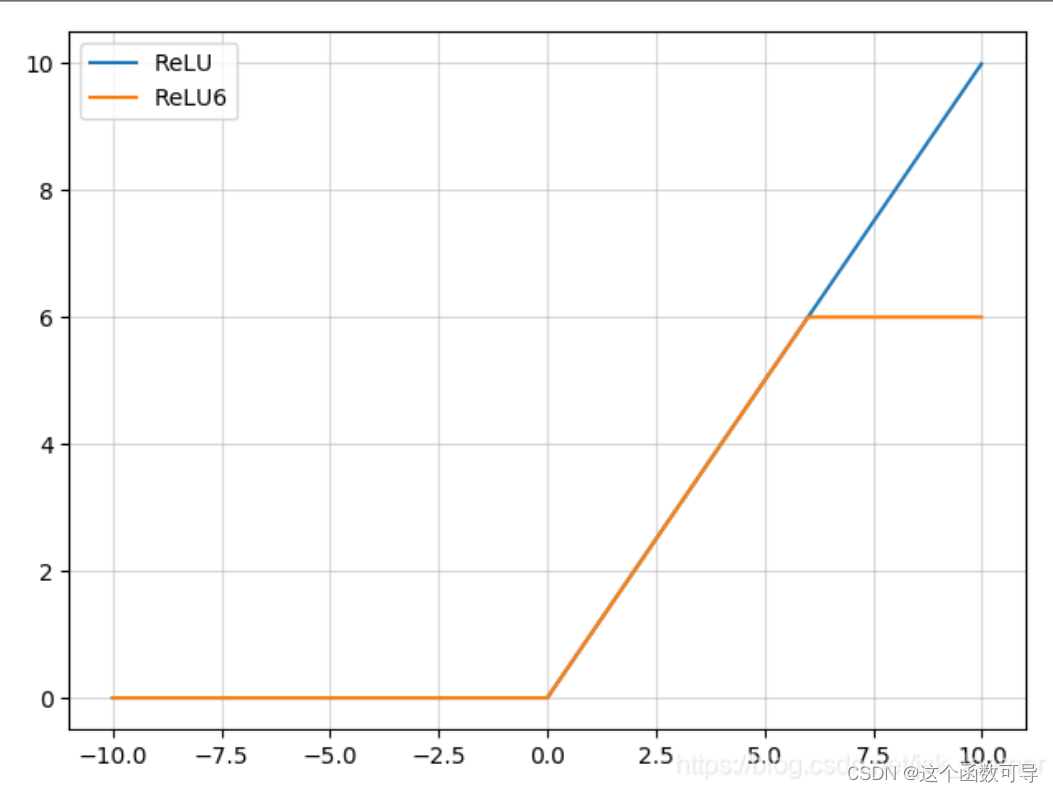
ReLU6
ReLU的正值输出为 [ 0 , + ∞ ) [0,+∞) [0,+∞),而计算机内存有限,并不能够存储无穷大的数,所以将ReLU应用到实际中需要限定输出的最大值,最大输出限定为6,就是ReLU6,如下图所示。
Leaky ReLU函数
为了缓解“死区”现象,Leaky ReLU尝试将ReLU的 x