【排序算法】深入解析快速排序（霍尔法&&三指针法&&挖坑法&&优化随机选key&&中位数法&&小区间法&&非递归版本）

文章目录

• 📝快速排序
• • 🌠霍尔法
  • 🌉三指针法
  • 🌠挖坑法
  • • ✏️优化快速排序
    • 🌠随机选key
    • • 🌉三位数取中
      • 🌠小区间选择走插入，可以减少90%左右的递归
      • 🌉 快速排序改非递归版本
      • 🚩总结

        ---

        📝快速排序

        快速排序是一种分治算法。它通过一趟排序将数据分割成独立的两部分,然后再分别对这两部分数据进行快速排序。

        本文将用3种方法实现：

        🌠霍尔法

        霍尔法是一种快速排序中常用的单趟排序方法，由霍尔先发现。

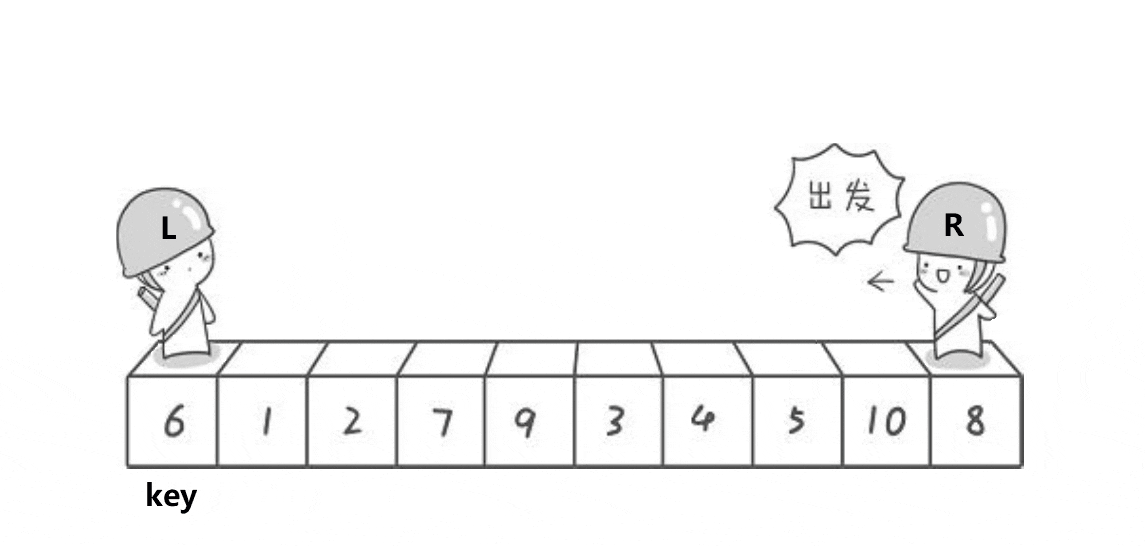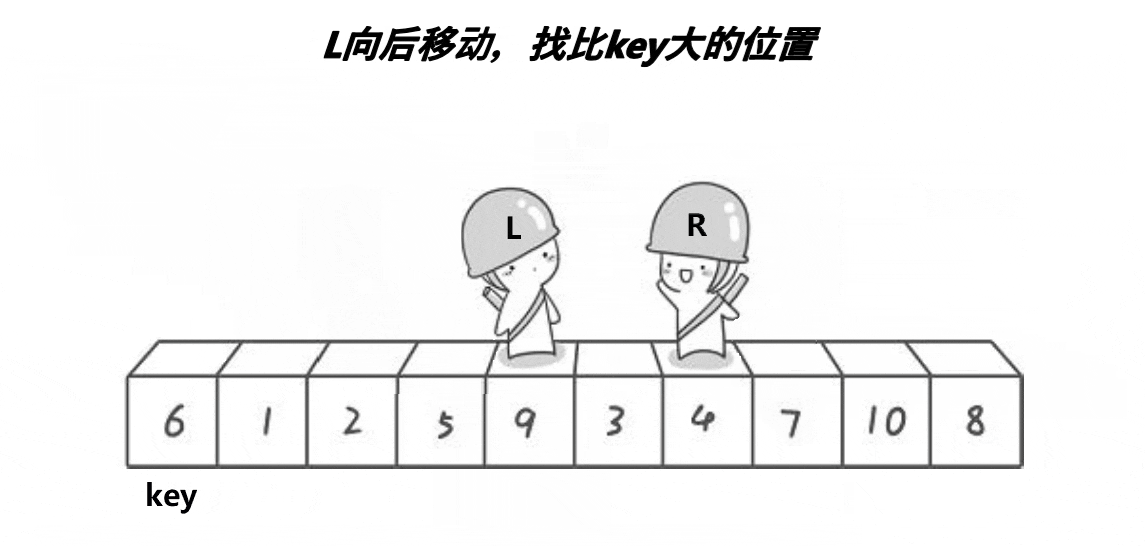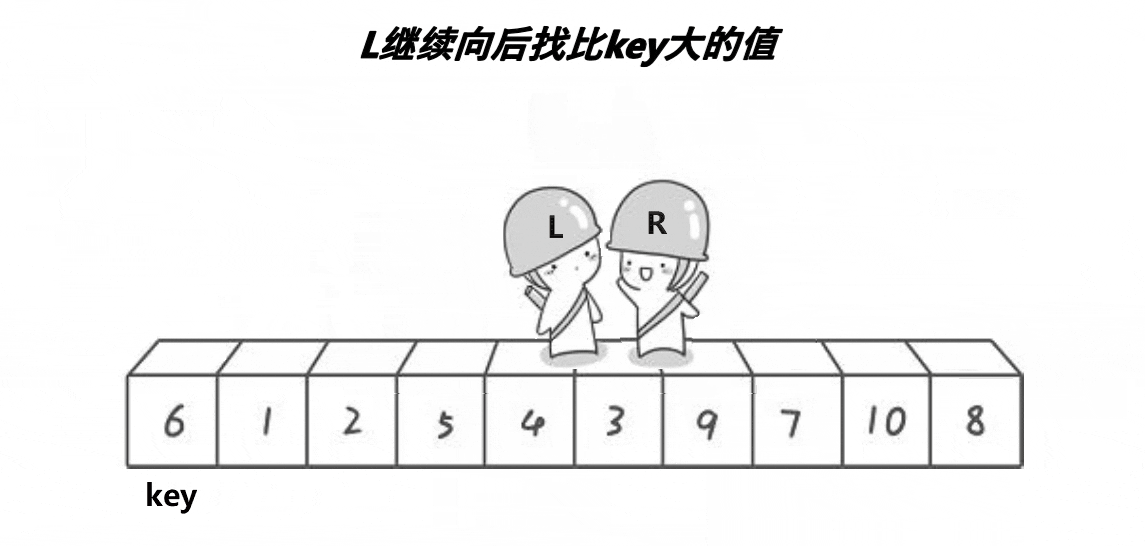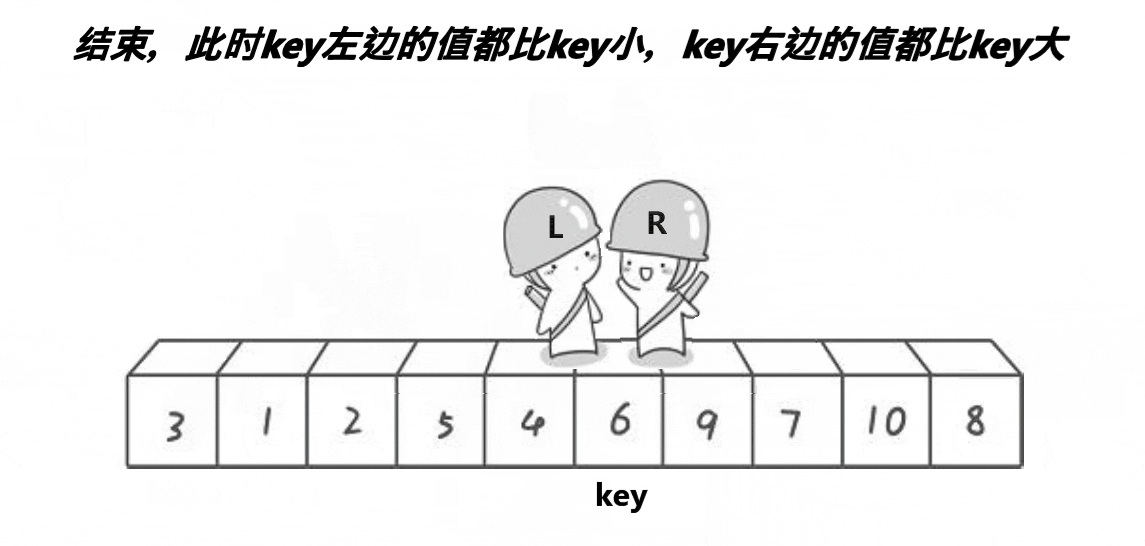
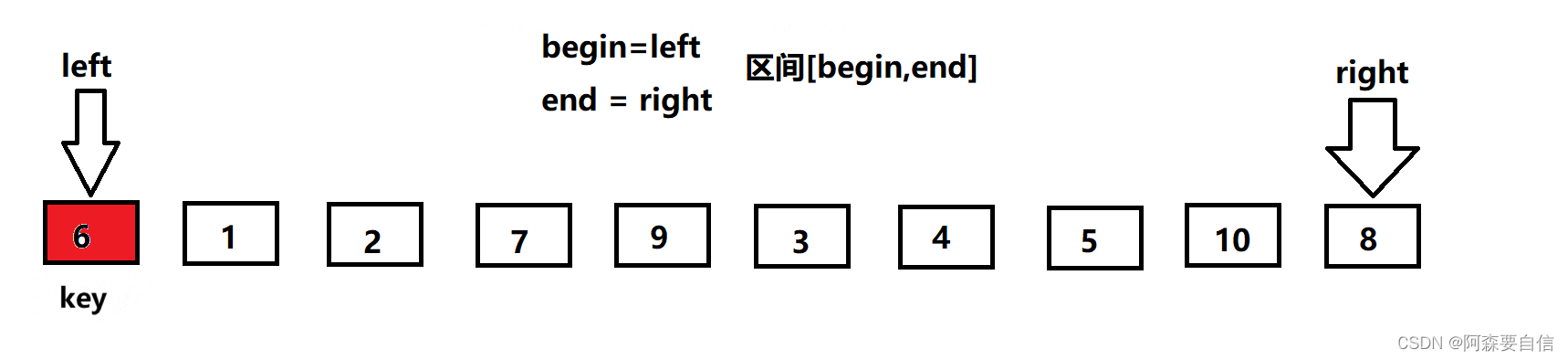
        它通过选定一个基准数key（通常是第一个元素），然后利用双指针left和right的方式进行排序，right指针先找比key基准值小的数，left然后找比key基准值大的数，找到后将两个数交换位置，同时实现大数右移和小数左移，当left与right相遇就排序完成，然后将下标key的值与left交换，返回基准数key的下标，完成了单趟排序。这一过程使得基准数左侧的元素都比基准数小，右侧的元素都比基准数大。

        如图动图展示：

        

        以下是单趟排序的详解图解过程：

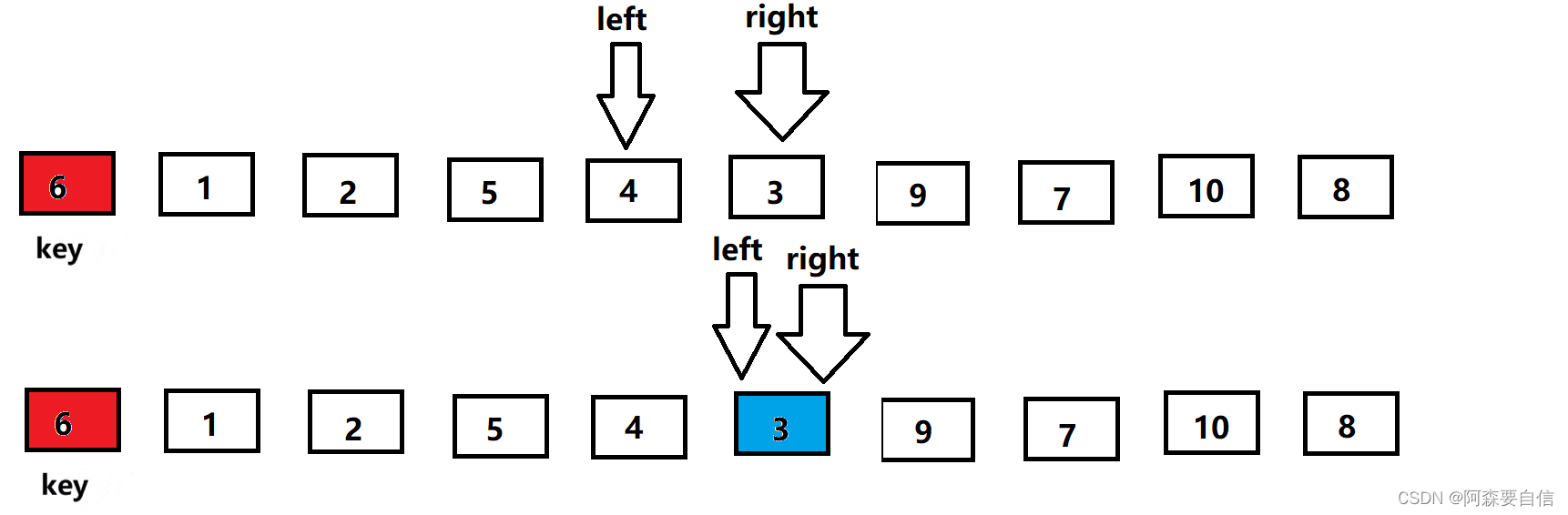
        • begin和end记录区间的范围，left记录做下标，从左向右遍历，right记录右下标，从右向左遍历，以第一个数key作为基基准值

          

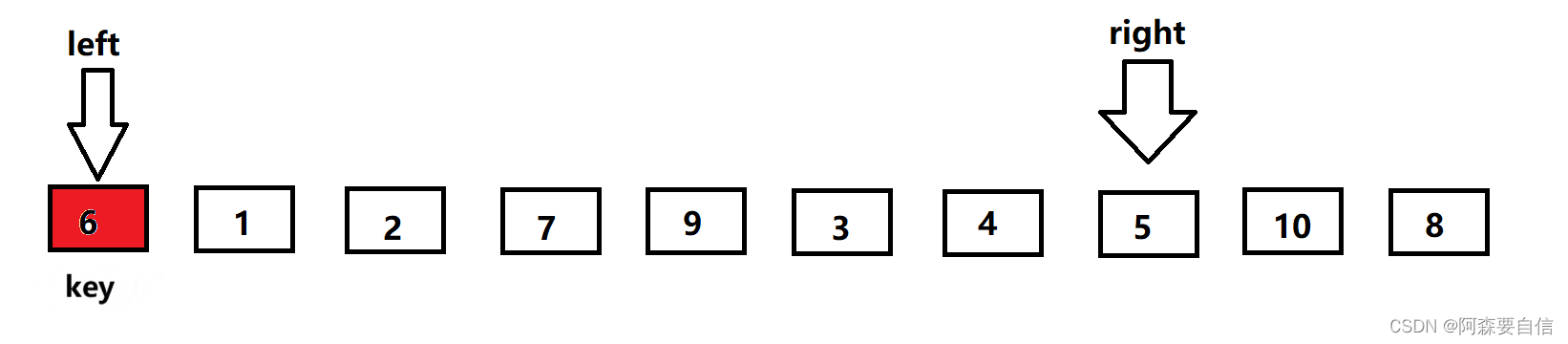
        • 先让right出发，找比key值小的值，找到就停下来

          

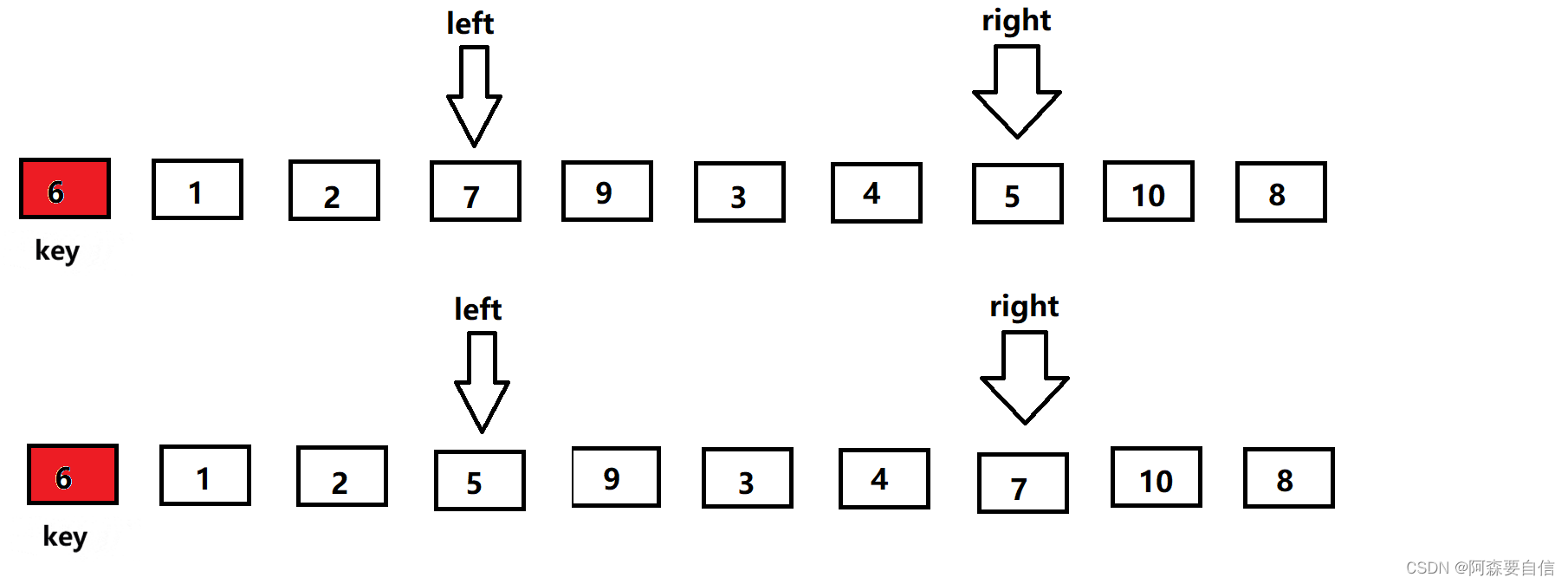
        • 然后left再出发，找比key大的值，若是找到则停下来，与right的值进行交换

          

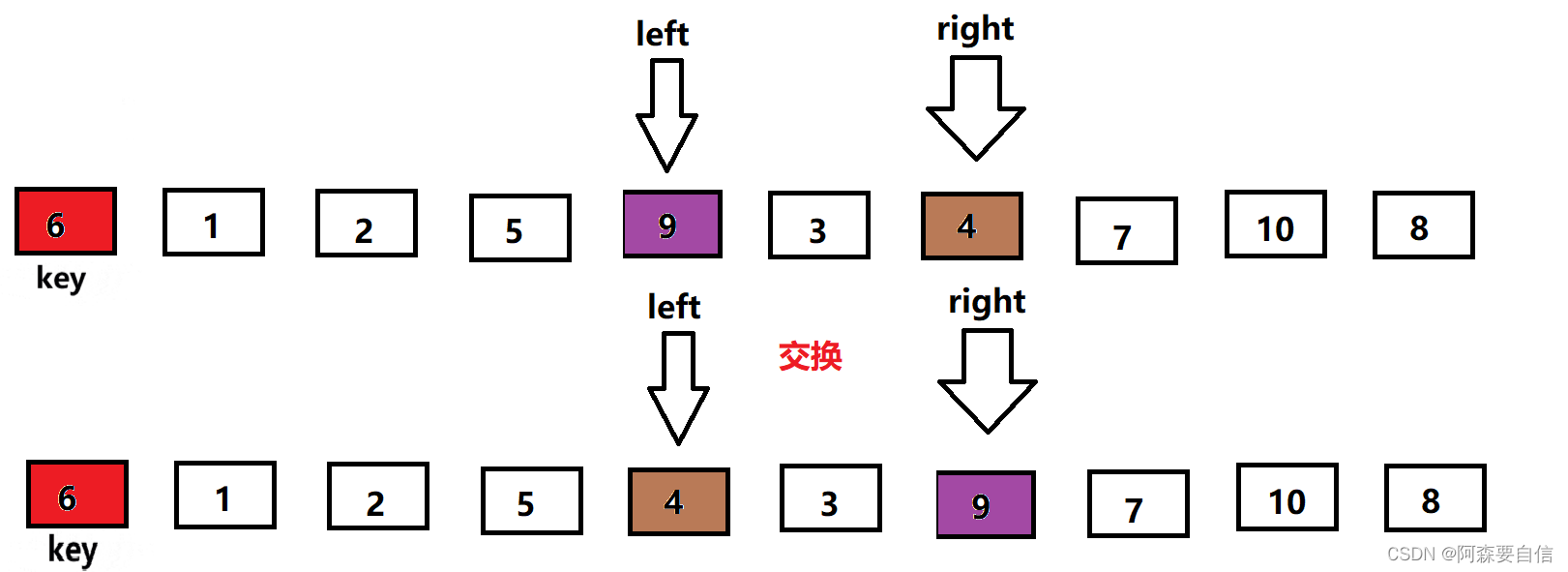
        • 接着right继续找key小的值，找到后才让left找比key大的值，直到left相遇right，此时left会指向同一个数

          

          

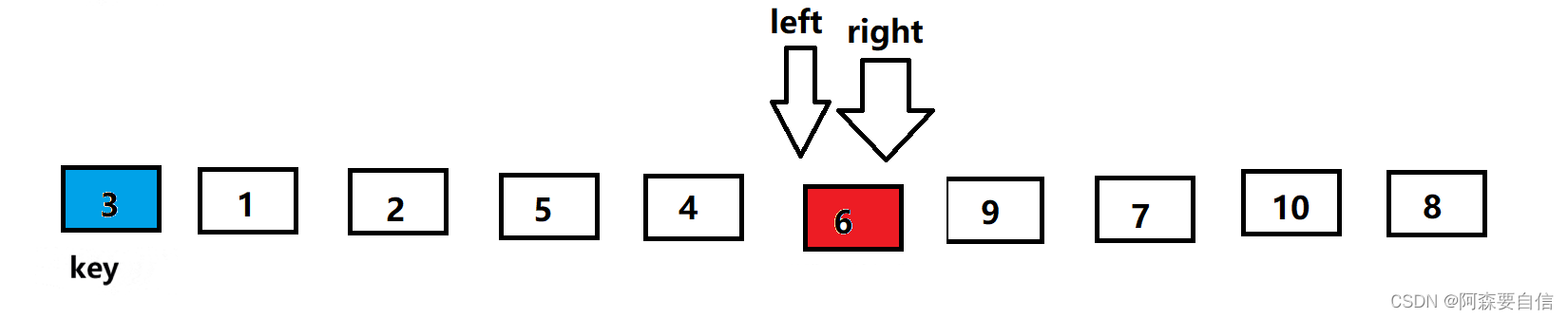
        • 将left与right指向的数与key进行交换，单趟排序就完成了，最后将基准值的下标返回

          

          为啥相遇位置比key要小->右边先走保证的

          1. L遇R: R先走,R在比key小的位置停下来了，L没有找到比key大的，就会跟R相遇相遇位置R停下的位置，是比key小的位置
          2. R遇L:第一轮以后的，先交换了，L位置的值小于key,R位置的值大于key ，R启动找小，没有找到，跟L相遇了，相遇位置L停下位置，这个位置比key小
          • 第一轮R遇L，那么就是R没有找到小的，直接就一路左移，遇到L，也就是key的位置

            代码实现

            void Swap(int* px, int* py)
            {
            	int tmp = *px;
            	*px = *py;
            	*py = tmp;
            }
            //Hoare经典随机快排
            void QuickSort1(int* a, int left, int right)
            {
            	// 如果左指针大于等于右指针,表示数组为空或只有一个元素,直接返回
            	if (left >= right)
            		return;
            	// 区间只有一个值或者不存在就是最小子问题
            	int begin = left, end = right;// begin和end记录原始整个区间
            	// keyi为基准值下标,初始化为左指针
            	int keyi = left;
            	 // 循环从left到right
            	while (left  
            取中的返回函数接收：
             
            		int begin = left, end = right;
            		// 三数取中
            		int midi = GetMidi(a, left, right);
            		//printf("%d\n", midi);
            		Swap(&a[left], &a[midi]);
             
            整体函数实现：
             
            //三数取中  left  mid  right
            //大小居中的值，也就是不是最大，也不是最小的
            int GetMid(int* a, int left, int right)
            {
            	int mid = (left + right) / 2;
            	
            	if (a[left]  a[right])
            		{
            			return left;
            		}
            		else
            		{
            			return  right;
            		}
            	}
            	else//a[left] > a[mid]
            	{
            		if (a[mid] > a[right])
            		{
            			return mid;
            		}
            		else if (a[right] > a[left])
            		{
            			return left;
            		}
            		else
            		{
            			return right;
            		}
            	}
            }
            void QuickSort4(int* a, int left, int right)
            {
            	if (left >= right)
            		return;
            	int begin = left, end = right;
            	//三数取中
            	int midi = GetMid(a, left, right);
            	//printf("%d\n",midi);
            	Swap(&a[left], &a[midi]);
            	int keyi = left;
            	while (left = a[keyi])
            		{
            			--right;
            		}
            		while (left = a[keyi])
            			{
            				--right;
            			}
            			while (left top = 0;
            	ps->capacity = 0;
            }
            void STDestroy(ST* ps)
            {
            	assert(ps);
            	free(ps->a);
            	ps->a = NULL;
            	ps->top = ps->capacity = 0;
            }
            // 栈顶
            void STPush(ST* ps, STDataType x)
            {
            	assert(ps);
            	// 满了， 扩容
            	if (ps->top == ps->capacity)
            	{
            		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
            		STDataType* tmp = (STDataType*)realloc(ps->a, newcapacity * sizeof(STDataType));
            		if (tmp == NULL)
            		{
            			perror("realloc fail");
            			return;
            		}
            		ps->a = tmp;
            		ps->capacity = newcapacity;
            	}
            	ps->a[ps->top] = x;
            	ps->top++;
            }
            void STPop(ST* ps)
            {
            	assert(ps);
            	assert(!STEmpty(ps));
            	ps->top--;
            }
            STDataType STTop(ST* ps)
            {
            	assert(ps);
            	assert(!STEmpty(ps));
            	return ps->a[ps->top - 1];
            }
            int STSize(ST* ps)
            {
            	assert(ps);
            	return ps->top;
            }
            bool STEmpty(ST* ps)
            {
            	assert(ps);
            	return ps->top == 0;
            }
             
            栈的头文件实现：
             
            #pragma once
            #include
            #include
            #include
            #include
            typedef int STDataType;
            typedef struct Stack
            {
            	STDataType* a;
            	int top;
            	int capacity;
            }ST;
            void STInit(ST* ps);
            void STDestroy(ST* ps);
            // 栈顶
            void STPush(ST* ps, STDataType x);
            void STPop(ST* ps);
            STDataType STTop(ST* ps);
            int STSize(ST* ps);
            bool STEmpty(ST* ps);
             
            🚩总结
             
            快速排序的特性总结：
             
            快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
            时间复杂度：O(N*logN)
            空间复杂度：O(logN)
            稳定性：不稳定
            因此
            时间复杂度：O(N*logN)
            什么情况快排最坏：有序/接近有序 ->O(N^2)
            但是如果加上随机选key或者三数取中选key，最坏情况不会出现，所以这里不看最坏
             
             
            快排可以很快，你的点赞也可以很快，哈哈哈，感谢💓 💗 💕 💞，喜欢的话可以点个关注，也可以给博主点一个小小的赞😘呀