动态规划课堂6-----回文串问题
目录
引言:
例题1:回文子串
例题2:回文串分割IV
例题3:分割回文串II
例题4:最长回文子序列
例题5:让字符串成为回文串的最小插入次数
引言:
回文字符串 是正着读和倒过来读一样的字符串。
动态规划的回文串问题一般是把子串是否是回文串的信息保持在dp表里面,所以更多的时候回文串的dp表只是起到一个辅助的作用,有一些题要利用回文串dp表再做一次动态规划,其实很多困难题某一些步骤都是可以动态规划来化简的。😎😎😎
例题1:回文子串
链接:回文子串
题目简介:
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
解法(动态规划):
当然这题的最优解不是动态规划而是中心拓展算法,但是我们这里主要叙述动态规划。
这一题其实就是一个把回文子串信息保存在dp表里面的模板题😎
对于本题我们可以先预处理⼀下,将所有子串是否回⽂的信息统计在dp 表⾥⾯,然后直接在表里面统计true 的个数即可。
1. 状态表示:
dp[i][j] 表示: s 字符串[i, j] 的子串,是否是回文串。
这个二维的dp表其实只需用到上三角的地方,因为j是大于等于i的。
2.状态转移方程:
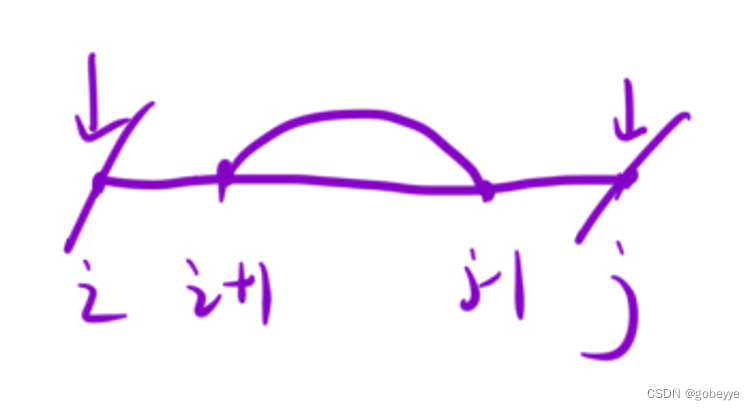
对于回文串,我们⼀般分析⼀个区间两头的元素:例如下图利用最外层和内层的递推关系完成动态规划。
(1)当s[i] != s[j] 的时候:不可能是回文串, dp[i][j] = 0 ;
(2)当s[i] == s[j] 的时候:根据长度分三种情况讨论:
1.⻓度为1 ,也就是i == j ,此时⼀定是回文串, dp[i][j] = true。
2.⻓度为2 ,也就是i + 1 == j :此时也⼀定是回⽂串, dp[i][j] = true 。
3.⻓度⼤于2 ,此时要去看看[i + 1, j - 1] 区间的子串是否回文: dp[i][j] = dp[i + 1][j - 1] 。
3.初始化:
无需初始化,因为我们填表的范围如下图,会越界的节点在对角线,但是我们上面的状态转移方程已经把i == j的情况特判了,所以不会越界。
4.填表顺序:
从下往上
5.返回值:
返回dp 表中true 的个数。
代码如下:
dp[i][j] = i + 1
class Solution {
public int countSubstrings(String ss) {
//1.创建 dp 表
//2.初始化
//3.填表
//4.返回值
int n = ss.length();
char[] s = ss.toCharArray();
boolean[][] dp = new boolean[n][n];
int count = 0;
for(int i = n - 1;i >= 0;i--){
for(int j = i;j
时间复杂度:O(n^2)
空间复杂度:O(n^2)
下面我给出一题大家练练手,解法过程和例题1差不多就是最后创建完回文dp表最后的返回值不一样。最长回文子串
例题2:回文串分割IV
链接:回文串分割IV
题目简介:
给你一个字符串 s ,如果可以将它分割成三个 非空 回文子字符串,那么返回 true ,否则返回 false 。
当一个字符串正着读和反着读是一模一样的,就称其为 回文字符串 。
关于预处理所有子串是否回文,已经在上⼀道题目里面讲过,这里就不再赘述啦~
先把回文dp表填好,接下来枚举三个子串除字符串端点外的起止点,查询这三段非空子串是否是回文串。 枚举i和j这两条分界线即可,注意区间的闭合问题和J必须要大于等于i。
代码如下:
1. 利用 dp 处理⼀下所有的子串是否回文。
2. 枚举第二个字符串所有的起始位置和终止位置。
写代码希望大家按照1.创建 dp 表2,初始化,3.填表,4.返回值的顺序来进行书写代码,这样不会乱。
class Solution {
public boolean checkPartitioning(String s) {
//1.创建 dp 表
//2.初始化
//3.填表
//4.返回值
int n = s.length();
boolean[][] dp = new boolean[n][n];
for(int i = n - 1;i >= 0;i--){
for(int j = i;j
时间复杂度:O(n^2)
空间复杂度:O(n^2)
例题3:分割回文串II
链接:分割回文串II
题目简介:
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串。
返回符合要求的 最少分割次数 。
解法(动态规划):
1. 状态表示:
dp[i] 表示: s中[0, i] 区间上的字符串,最少分割的次数。
2.状态转移方程:
状态转移方程⼀般都是根据最后⼀个位置的信息来分析:设0 = j - 1 ? 1 : dp[i + 1][j - 1]。
(2)s[i] != s[j]时: dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1 。
3.初始化:
没有不能递推表示的值,无需初始化。
4.填表顺序:
从下往上填写每⼀行
从下往上填写每⼀行
5.返回值:
返回dp[0][n - 1]。
代码如下:
class Solution {
public int minInsertions(String s) {
//1.创建 dp 表
//2.初始化
//3.填表
//4.返回值
int n = s.length();
int[][] dp = new int[n][n];
for(int i = n - 1;i >= 0;i--){
for(int j = i;j
时间复杂度:O(n^2)
空间复杂度:O(n^2)
结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固知识点,和做一个学习的总结,由于作者水平有限,对文章有任何问题还请指出,非常感谢。如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。