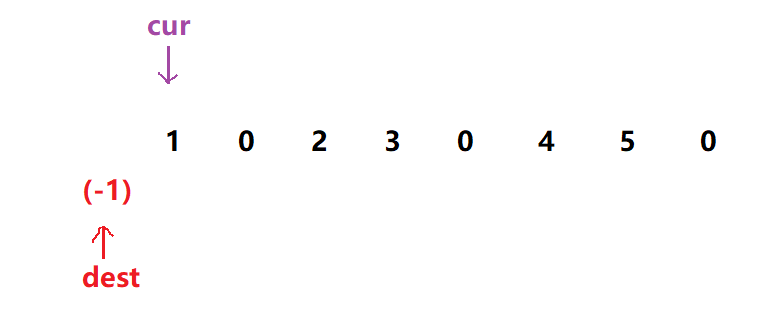【优选算法】专题1 -- 双指针 -- 复写0

04-10 1232阅读

前言：

补充一下前文没有写到的双指针入门知识：专题1 -- 双指针 -- 移动零

基础入门知识：

1. 复写零（easy）

1. 题⽬链接：1089.复习0 - 力扣（LeetCode）

2. 题⽬描述：

3.算法原理：

异地操作

本地操作

【从后向前的复写过程】

整体思路：

🎯1.先找到最后一个“复写”的数;

1.5 处理一下边界情况:

📌2."从后向前"完成复写操作（前面已经验证)

基础入门知识：

常⻅的双指针有两种形式，⼀种是对撞指针，⼀种是左右指针。

对撞指针：⼀般⽤于顺序结构中，也称左右指针。

• 对撞指针从两端向中间移动。⼀个指针从最左端开始，另⼀个从最右端开始，然后逐渐往中间逼近。

• 对撞指针的终⽌条件⼀般是两个指针相遇或者错开（也可能在循环内部找到结果直接跳出循环），也就是：

◦ left == right （两个指针指向同⼀个位置）

◦ left > right （两个指针错开）

快慢指针：⼜称为⻳兔赛跑算法

其基本思想：就是使⽤两个📌移动速度📌不同的指针在数组或链表等序列结构上移动。

💨这种⽅法对于处理环形链表或数组⾮常有⽤。

其实不单单是环形链表或者是数组，⭕如果我们要研究的问题出现循环往复的情况时，均可考虑使⽤快慢指针的思想。

📍快慢指针的实现⽅式有很多种，最常⽤的⼀种就是：

• 在⼀次循环中，每次让慢的指针向后移动⼀位，⽽快的指针往后移动两位，实现⼀快⼀慢

1. 复写零（easy）

1. 题⽬链接：1089.复习0 - 力扣（LeetCode）

2. 题⽬描述：

给你⼀个⻓度固定的整数数组 arr ，请你将该数组中出现的每个零都复写⼀遍，并将其余的元素向右平移。

注意：请不要在超过该数组⻓度的位置写⼊元素。请对输⼊的数组就地进⾏上述修改，不要从函数返回任何东西。

⽰例 1：

输⼊： arr = [1,0,2,3,0,4,5,0]

输出： [1,0,0,2,3,0,0,4]

解释：

调⽤函数后，输⼊的数组将被修改为： [1,0,0,2,3,0,0,4]

3.算法原理：

这题需要用到双指针算法，但这不是凭空来的，原题目需要我们对原数组进行操作，

异地操作

📚但是为了方便如何理解复写 0 的过程，我们先画出异地操作的过程：

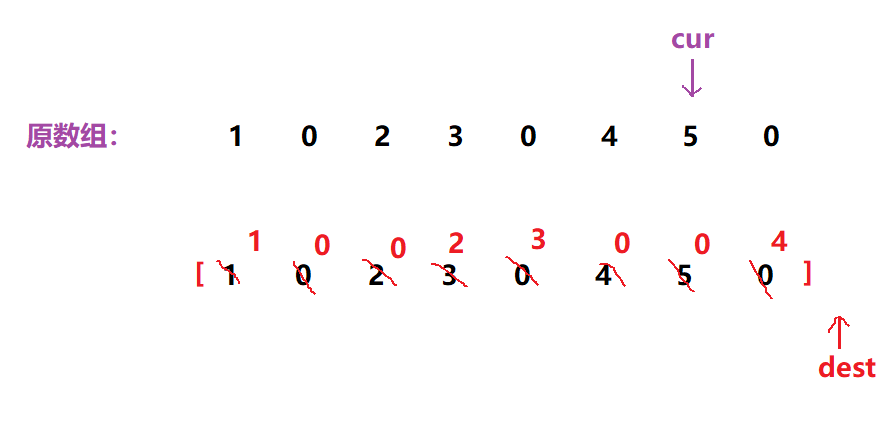
原图：

复写过程：

cur用于遍历原数组，dest指向了异地操作的数组，

当cur指向的元素为非0时，dest此时要复写一次cur指向的非0元素，cur++,dest++

当cur指向的元素为 0 时，dest要先复写一次0,之后dest++，再复写一次0，复写两次完毕之后cur++，dest++

复写完成：

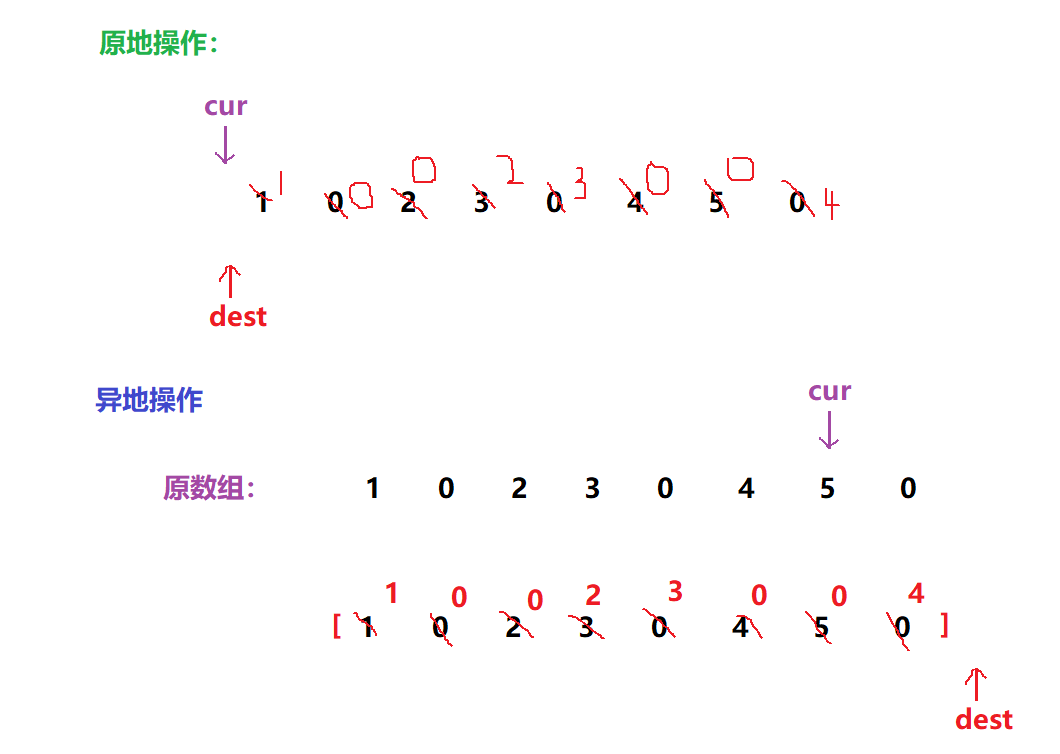
本地操作

优化为本地操作后，尝试从前往后操作：

如果「从前向后」进⾏原地复写操作的话，由于 0 的出现会复写两次，导致没有复写的数「被覆盖掉」。

验证【从后往前】操作的可行性:

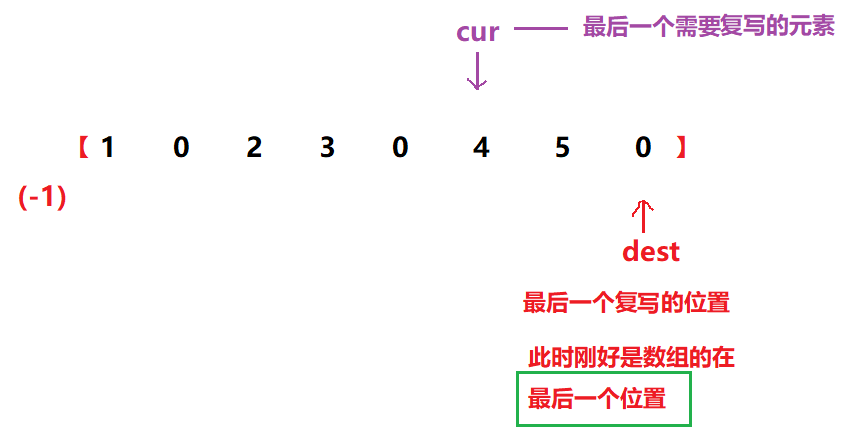
因此我们选择「从后往前」的复写策略，cur指向最后一个需要复写的元素，dest指向最后一个需要复写的位置(结果中的最后一个位置)

这同时也是上面异地操作的结果：

【从后向前的复写过程】

结果：我们可以看到，原地操作和异地操作最终的复写结果是一样的

在这个示例里面，我们可以看到cur指向的4是最后一个需要复写的元素，但是在其他示例里面我们不清楚，那么我们如何找到最后一个需要复写的元素呢？

整体思路：

🎯1.先找到最后一个“复写”的数;

1.先判断 cur 位置的值

2.决定 dest 向后移动一步或者两步

3.判断一下 dest 是否已经到结束为止

4.cur++；

开始的状态：

遍历过程(动图实现):

最终的状态：

但是思考一下，此时如果cur指向的数组倒数第二个元素是0，那么dest此时指向的位置将会是数组最后一个元素的位置的下一个位置,因为上面遍历的方式是遇到 0 则++两次，非0是一次，那么必定会造成数组越界：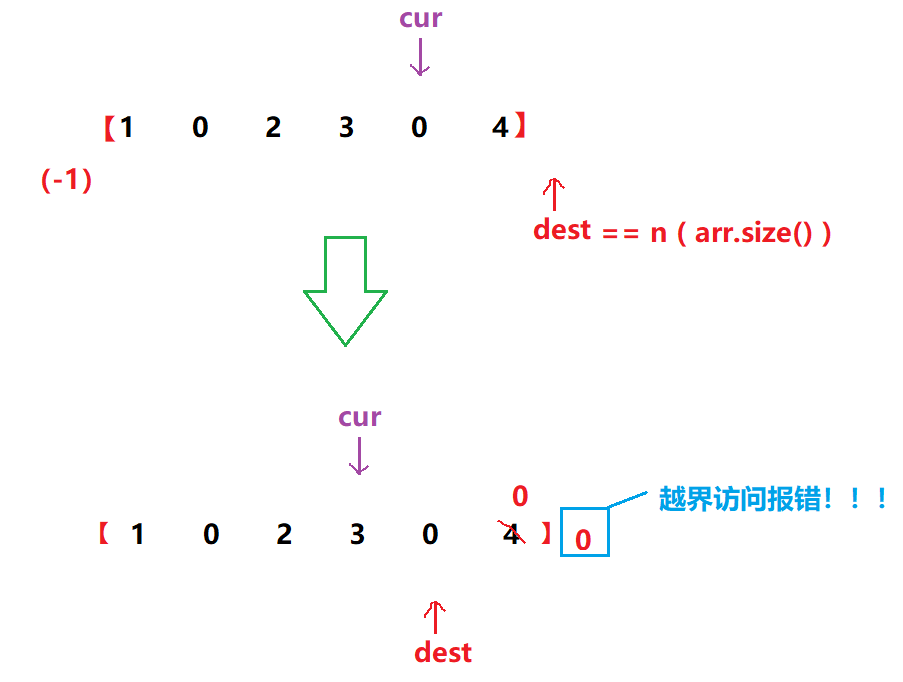

1.5 处理一下边界情况:

arr[n - 1] = 0;

cur--;

dest -= 2;

📌2."从后向前"完成复写操作（前面已经验证)

代码实现：

class Solution {
public:
    void duplicateZeros(vector& arr) {
    int cur = 0,dest = -1,n=arr.size();
    
    //1.先找到最后一个需要复写的数
    while(cur=n-1)//数组最后一个位置或者最后一个位置的下个位置
            break;
        cur++;
        }
    //2.处理一下边界情况
    if(dest == n)
    {
        arr[n-1] = 0;
        cur--;
        dest-=2;
    }
    //3.从后往前完成复写操作
    while(cur >= 0)
    {
        if(arr[cur])
        {
           arr[dest--] = arr[cur--];
           //arr[dest] = arr[cur],cur--,dest--
        }
        else
        {
           arr[dest--] = 0;
           arr[dest--] = 0;
           cur--;
        }
    }
    }
};