数据结构——认识二叉树

这是一篇回顾二叉树概念的文章

• 前言：
• 一、了解树形结构
• • 1.2 树的定义
  • 2.2 树的相关概念
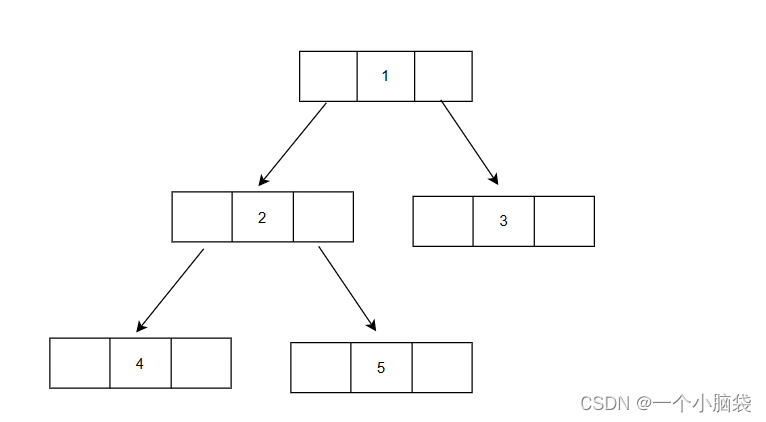
  • 2.2 树的表示形式
  • 二、了解二叉树结构和性质
  • • 2.1 什么是二叉树？
    • 2.2 二叉树的性质
    • 2.3 二叉树的遍历
    • 2.3 二叉树的应用范围
    • 2.5 二叉树的优缺点
    • 三、掌握二叉树的存储结构
    • • 3.1 二叉树的顺序结构存储
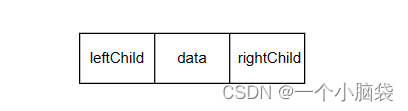
      • 3.2 二叉树的链式结构存储

        前言：

        一、了解树形结构

        1.2 树的定义

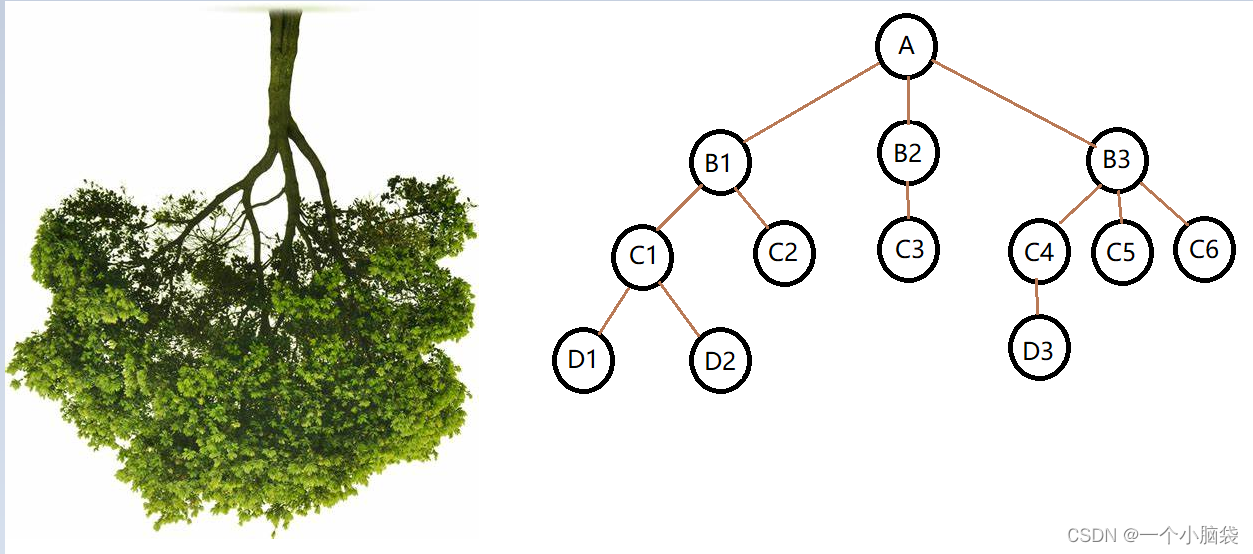
        树是一种非线性的数据结构，它是由 n （ n>=0 ）个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的

        

        它具有以下的特点：

        • 有一个特殊的结点，称为根结点，根结点没有前驱结点。
        • 除根结点外，其余结点被分成M(M >0)个互不相交的集合T1、T2、…、Tm，其中每一个集合Ti (1 0)个结点。
        • 若规定根结点的层数为1，则深度为K的二叉树的最大结点数是2^k-1(一共有多少个结点）
        • 对任何一棵二叉树, 如果其叶子结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1（度为0的比度为2的永远多一个）
        • 若规定根结点的层数为1，具有n个结点的满二叉树的深度，h=long2（n+1）（2为底，n+1为指数）
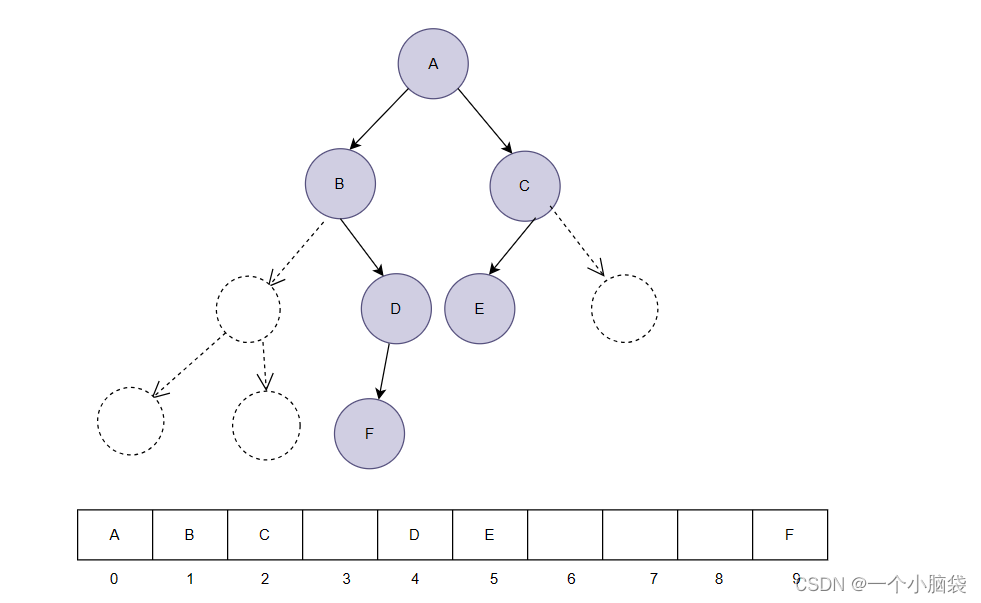
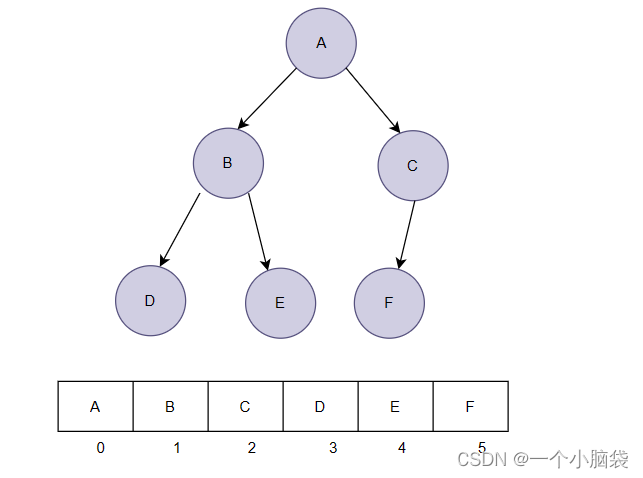
        • 对具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有结点从0开始编号，则有：

          通过下标任意位置可以找孩子和父亲

          

        2.3 二叉树的遍历

        前序遍历（Preorder Traversal）：

        • 访问根节点
        • 前序遍历左子树
        • 前序遍历右子树

          2. 中序遍历（Inorder Traversal）：

          • 中序遍历左子树
          • 访问根节点
          • 中序遍历右子树

            3. 后序遍历（Postorder Traversal）：

            • 后序遍历左子树
            • 后序遍历右子树
            • 访问根节点

              2.3 二叉树的应用范围

              1. 数据库系统： 二叉树结构在数据库系统中常用于索引结构，例如二叉搜索树。
              2. 表达式树：用于表示数学表达式，其中每个操作符是树的一个节点，操作数是它的子节点。
              3. 文件系统：文件系统中的目录结构通常可以用树来表示，例如Unix文件系统。
              4. 编译器设计：语法树（语法分析树）是编译器中用于表示源代码结构的一种二叉树。
              5. 网络路由算法： 用于构建路由表，支持高效的数据包转发。

              2.5 二叉树的优缺点

              优点：

              高效的搜索： 二叉树的结构使得搜索操作非常高效，因为每个节点都最多有两个子节点，可以通过比较大小迅速确定搜索方向。

              易于排序： 二叉搜索树（BST）的一种形式，能够在插入和删除操作中维护排序。

              缺点：

              不平衡可能性： 在某些情况下，二叉树可能会退化为链表，导致操作的时间复杂度变为O(n)。

              对于特定类型的数据集，性能可能下降： 当数据集合中的数据顺序有序时，二叉树的性能可能变差，因为它将导致树的不平衡。

              三、掌握二叉树的存储结构

              二叉树的存储结构可以分为两大类：

              • 顺序结构存储
              • 链式结构存储

                3.1 二叉树的顺序结构存储

                二叉树的顺序存储对二叉树是有一定要求的，普通的二叉树不适合使用顺序存储，会造成空间上的浪费。（二叉树顺序存储，在物理上是一个数组，在逻辑上是一颗二叉树）

                如图：

                

                只有完全二叉树才可以使用顺序存储

                如图：

                

                3.2 二叉树的链式结构存储

                二叉树的链式存储结构，顾名思义就是使用链表来表示二叉树，使用链表来表示二叉树的结构，通常是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。