GRU门控循环单元神经网络的MATLAB实现（含源代码）

在深度学习领域，循环神经网络（RNN）因其在处理序列数据方面的卓越能力而受到广泛关注。GRU（门控循环单元）作为RNN的一种变体，以其在捕捉时间序列长距离依赖关系方面的高效性而备受推崇。在本文中，我们将探讨如何在MATLAB环境中实现GRU网络，以及该实现在处理各类序列数据时的应用。

GRU神经网络简介

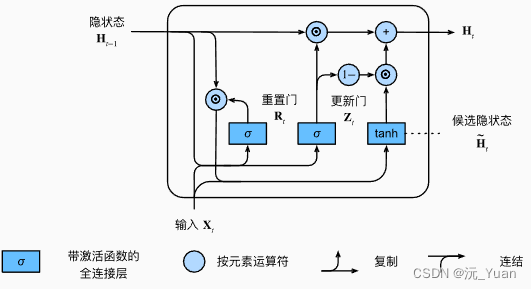
GRU由Cho等人于2014年提出，旨在解决标准RNN在处理长序列时的梯度消失或梯度爆炸问题。与传统的RNN相比，GRU引入了两个关键的门控机制：更新门（Update Gate）和重置门（Reset Gate）。这些门控结构帮助模型更有效地捕捉长期依赖关系。

更新门

更新门负责决定信息的保留量。它决定了来自过去状态的信息应该被多大程度上保留，以及新的候选隐藏状态的信息应该被多大程度上加入。

重置门

重置门则决定了多少过去的信息需要被忽略。它可以帮助模型忘记无关的信息，从而专注于当前的重要信息。

MATLAB中的GRU实现

在MATLAB中实现GRU涉及以下关键步骤：

数据准备：首先，我们需要准备并预处理适合GRU模型的序列数据。这通常包括数据的归一化、划分训练集和测试集等。

模型构建：MATLAB提供了内置的GRU层，可以通过gruLayer函数轻松创建。用户可以指定神经元数量、激活函数等参数。

模型训练和调整：利用MATLAB的trainingOptions函数，我们可以定义训练参数，如学习率、迭代次数、批大小等。然后，使用trainNetwork函数开始训练过程。在此阶段，调整模型参数和结构以达到最佳性能是至关重要的。

性能评估和测试：在模型训练完成后，需要在测试集上评估其性能。这通常涉及计算诸如准确率、损失函数值等指标，并对模型进行必要的微调。

应用和部署：训练好的GRU模型可以应用于各种序列数据任务，如时间序列预测、语言建模、情感分析等。MATLAB支持将训练好的模型导出，以便在其他应用中使用。

MATLAB中实现GRU的关键

在MATLAB中实现GRU时，有几个关键因素需要考虑：

数据预处理：确保输入数据格式适合MATLAB处理。适当的标准化或归一化可以提高模型的学习效率和性能。

超参数选择：合适的超参数（如隐藏层神经元数、学习率、批大小等）对模型的性能有重大影响。可能需要通过实验来找到最优设置。

避免过拟合：使用诸如dropout层或正则化技术来避免过拟合，特别是在处理小型数据集时。

计算资源：GRU模型训练可能需要较高的计算资源，特别是对于大型数据集。。

结论

GRU门控循环单元神经网络是一种强大的工具，适用于各种复杂的序列数据处理任务。在MATLAB中实现GRU不仅可行，而且相对直接，得益于MATLAB提供的高级函数和易于使用的界面。通过正确的实现和调整，GRU模型可以在多种应用中展现出色的性能，从而揭示序列数据的深层次特征和模式。

部分源代码

%% GRU参数设置
%% 清空环境变量
	clc;
	clear;
	close all;
	warning off;
	tic
	
%% 导入数据
	load data.mat
	[trainInd,valInd,testInd] = dividerand(size(X,2),0.7,0,0.3);	%划分训练集与测试集
	input_train = X(:,trainInd);	%列索引
	output_train = Y(:,trainInd);
	input_test = X(:,testInd);
	output_test = Y(:,testInd);
%% 归一化
	[inputn_train,input_ps] = mapminmax(input_train);	%映射到[0,1]并把参数保存到input_ps中
	[outputn_train,output_ps] = mapminmax(output_train);
	inputn_test = mapminmax('apply',input_test,input_ps);	%将归一化参数input_ps应用到测试集输入数据中
	outputn_test = mapminmax('apply',output_test,output_ps);
%% GRU参数设置
	inputSize = size(inputn_train,1);	%输入数据维度
	outputSize = size(outputn_train,1);		%输出数据维度
	numhidden_units = 5;
	
    layers = [ ...
        sequenceInputLayer(inputSize)                 %输入层设置
        gruLayer(numhidden_units,'Outputmode','sequence','name','hidden') 
        reluLayer('name','relu')
        fullyConnectedLayer(outputSize)               % 全连接层设置（影响输出维度）
        regressionLayer('name','out')];
		
	opts = trainingOptions('adam', ...
		'MaxEpochs',200, ...
		'ExecutionEnvironment','cpu',...
		'InitialLearnRate',0.1, ...
		'LearnRateSchedule','piecewise', ...
		'LearnRateDropPeriod',180, ...                % 学习率更新
		'LearnRateDropFactor',0.2, ...
		'Verbose',1, ...
		'Plots','training-progress'... 
		);
		
	analyzeNetwork(layers);	%显示网络结构
	
%% GRU网络训练
	GRUnet = trainNetwork(inputn_train,outputn_train,layers,opts);	
	
	[GRUnet,GRUoutputr_train] = predictAndUpdateState(GRUnet,inputn_train);	%训练集训练
	GRUoutput_train = mapminmax('reverse',GRUoutputr_train,output_ps);
	[GRUnet,GRUoutputr_test] = predictAndUpdateState(GRUnet,inputn_test);	%测试集训练
	GRUoutput_test = mapminmax('reverse',GRUoutputr_test,output_ps);
%% 输出数据
    len=size(output_test,2);
	error1 = GRUoutput_test - output_test;	%GRU网络输出误差
	error2 = GRUoutput_train - output_train;
    MAE1=sum(abs(error1./output_test))/len;
	MAPE1 = calculateMAPE(output_test,GRUoutput_test);
	RMSE1 = sqrt(mean((error1).^2));
	disp('GRU网络测试集预测绝对平均误差MAE');
	disp(MAE1);
	disp('GRU网络测试集预测平均绝对误差百分比MAPE');
	disp(MAPE1);
	disp('GRU网络测试集预测均方根误差RMSE');
	disp(RMSE1);
%% 输出可视化
	figure(1)
	plot(GRUoutput_test,'k');
	hold on;
	plot(output_test,'r');
    legend('预测值','真实值');
    title('测试集预测结果');
	hold on;
	
	figure(2)
	plot(error1);
    title('测试集误差');
	hold on;
    figure(3)
	plot(GRUoutput_train,'k');
	hold on;
	plot(output_train,'r');
    legend('预测值','真实值');
    title('训练集预测结果');
	hold on;
	
	figure(4)
	plot(error2);
    title('训练集误差');
	hold on;
    toc
function mape = calculateMAPE(actual, forecast)
    absolute_error = abs(actual - forecast);
    percentage_error = absolute_error ./ actual;
    mape = mean(percentage_error) * 100;
end

另外此处还有BIGRU,贝叶斯优化的GRU，BIGRU等代码，欢迎访问~~：https://mbd.pub/o/author-a2yXmm5naw==/work