【机器学习】数据探索---python主要的探索函数
温馨提示:这篇文章已超过389天没有更新,请注意相关的内容是否还可用!
在上一篇博客【机器学习】数据探索(Data Exploration)—数据质量和数据特征分析中,我们深入探讨了数据预处理的重要性,并介绍了诸如插值、数据归一化和主成分分析等关键技术。这些方法有助于我们清理数据中的噪声、消除异常值,以及降低数据的维度,从而为后续的机器学习模型训练提供更有价值的信息。
然而,数据预处理只是数据探索的一部分。在本篇博客中,我们将进一步探讨Python中一些主要的探索函数,这些函数将帮助我们更深入地理解数据的分布、特征之间的关系,以及数据中可能存在的模式。而在Python的数据探索领域,Pandas和Matplotlib是两个不可或缺的库。Pandas以其强大的数据处理和分析能力著称,而Matplotlib则以其出色的数据可视化功能闻名。Pandas中的函数可以大致分为两类:统计特征函数和统计作图函数。这些作图函数常常与Matplotlib紧密结合,共同呈现数据的内在规律和特点。下面,我们将详细介绍Pandas中的一些主要统计特征函数与统计作图函数,并通过实例来加深理解。这些函数不仅能够帮助我们深入了解数据的分布情况,还能揭示数据之间的潜在关系,为数据分析和机器学习模型的构建提供有力的支持。
一、 基本统计特征函数
统计特征函数用于计算数据的均值、方差、标准差、分位数、相关系数和协方差等,这些统计特征能反映出数据的整体分布。本小节所介绍的统计特征函数如表3-8所示,它们主要作为Pandas的对象DataFrame或 Series的方法出现。
P a n d a s 主要统计特征函数 \bold{Pandas主要统计特征函数} Pandas主要统计特征函数
| 方法名 | 函数功能 | 所属库 |
|---|---|---|
| sum() | 计算数据样本的总和(按列计算) | Pandas |
| mean() | 计算数据样本的算术平均数 | Pandas |
| var() | 计算数据样本的方差 | Pandas |
| std() | 计算数据样本的标准差 | Pandas |
| corr() | 计算数据样本的Spearman (Pearson)相关系数矩阵 | Pandas |
| cov() | 计算数据样本的协方差矩阵 | Pandas |
| skew() | 样本值的偏度(三阶矩) | Pandas |
| kurt() | 样本值的峰度(四阶矩) | Pandas |
| describe() | 给出样本的基本描述(基本统计量如均值、标准差等) | Pandas |
以下是Pandas库中一些主要统计特征函数的详细介绍,包括它们的功能、使用格式以及示例。
1.1 sum()
功能:计算Series或DataFrame中所有元素的和。
使用格式:
Series.sum() DataFrame.sum(axis=0, skipna=None, level=None, numeric_only=None, **kwargs)
- axis: 默认为0,表示按列求和;如果为1,则按行求和。
- skipna: 排除缺失值(NaN)进行计算,默认为True。
- numeric_only: 仅对数值列进行操作,默认为False。
示例:
import pandas as pd # 创建一个简单的DataFrame df = pd.DataFrame({'A': [1, 2, 3], 'B': [4, 5, 6]}) # 计算所有元素的和 sum_all = df.sum() print(sum_all) # 输出:A 6, B 15, dtype: int64 # 按行求和 sum_rows = df.sum(axis=1) print(sum_rows) # 输出:0 5, 1 7, 2 9, dtype: int641.2 mean()
**功能:**计算Series或DataFrame中所有元素的平均值。
使用格式:
Series.mean(skipna=None, level=None, numeric_only=None, **kwargs) DataFrame.mean(axis=0, skipna=None, level=None, numeric_only=None, **kwargs)
- axis: 默认为0,表示按列求平均值;如果为1,则按行求平均值。
- skipna: 排除缺失值(NaN)进行计算,默认为True。
- numeric_only: 仅对数值列进行操作,默认为False。
示例:
# 使用前面的DataFrame mean_col = df.mean() print(mean_col) # 输出:A 2.0, B 5.0, dtype: float64 mean_row = df.mean(axis=1) print(mean_row) # 输出:0 2.5, 1 3.5, 2 4.5, dtype: float64
1.3 var()
**功能:**计算Series或DataFrame中所有元素的方差。
使用格式:
Series.var(skipna=None, level=None, ddof=1, numeric_only=None, **kwargs) DataFrame.var(axis=0, skipna=None, level=None, ddof=1, numeric_only=None, **kwargs)
- axis: 默认为0,表示按列求方差;如果为1,则按行求方差。
- skipna: 排除缺失值(NaN)进行计算,默认为True。
- ddof: 自由度调整值,默认为1。
- numeric_only: 仅对数值列进行操作,默认为False。
示例:
var_col = df.var() print(var_col) # 输出方差计算结果
1.4 std()
**功能:**计算Series或DataFrame中所有元素的标准差。
使用格式:
Series.std(skipna=None, level=None, ddof=1, numeric_only=None, **kwargs) DataFrame.std(axis=0, skipna=None, level=None, ddof=1, numeric_only=None, **kwargs)
参数与var()函数相似。
示例:
std_col = df.std() print(std_col) # 输出标准差计算结果
1.5 corr()
**功能:**计算DataFrame中不同列之间的相关系数矩阵。
使用格式:
DataFrame.corr(method='pearson', min_periods=1)
- method: 计算相关系数的方法,默认为’pearson’皮尔逊相关系数,还可是’kendall’或’spearman’。
- min_periods: 一对列至少需要多少个非NA观测值才能计算相关系数。
示例:
corr_matrix = df.corr() print(corr_matrix) # 输出相关系数矩阵
1.6 cov()
**功能:**计算DataFrame中不同列之间的协方差矩阵。
使用格式:
DataFrame.cov(min_periods=None)
- min_periods: 一对列至少需要多少个非NA观测值才能计算协方差。
-
示例:
cov_matrix = df.cov() print(cov_matrix) # 输出协方差矩阵
1.7 skew()
**功能:**计算Series或DataFrame中所有数值列的偏度。偏度衡量数据分布的不对称性。
使用格式:
Series.skew(skipna=True, level=None, numeric_only=None, **kwargs) DataFrame.skew(axis=0, skipna=None, level=None, numeric_only=None, **kwargs)
- axis: 默认为0,表示按列计算偏度;如果为1,则按行计算偏度。
- skipna: 排除缺失值(NaN)进行计算,默认为True。
- numeric_only: 仅对数值列进行操作,默认为False。
示例:
skewness = df.skew() print(skewness) # 输出偏度计算结果
1.8 kurt()
**功能:**计算Series或DataFrame中所有数值列的峰度。峰度衡量数据分布形态的陡峭程度。
使用格式:
Series.kurt(skipna=True, level=None, numeric_only=None, **kwargs) DataFrame.kurt(axis=0, skipna=None, level=None, numeric_only=None, **kwargs)
参数与skew()函数相似。
示例:
kurtosis = df.kurt() print(kurtosis) # 输出峰度计算结果
1.9 describe()
**功能:**生成描述性统计信息,包括计数、均值、标准差、最小值、四分位数(25%、50%、75%)以及最大值。
使用格式:
DataFrame.describe(percentiles=[], include=[], exclude=None)
- percentiles: 要包含在输出中的百分位数。
- include: 要包含的列的数据类型。
- exclude: 要排除的列的数据类型。
示例:
desc_stats = df.describe() print(desc_stats) # 输出描述性统计信息
以上就是对Pandas库中一些主要统计特征函数的详细介绍和示例。这些函数在处理数据时非常有用,能够帮助我们快速了解数据的分布情况,为后续的数据分析和建模提供有力的支持。在使用这些函数时,可以根据具体的数据和需求选择合适的参数和选项。
二、拓展统计特征函数
除了上述基本的统计特征外,Pandas还提供了一些非常方便实用的计算统计特征的函数,主要有累积计算(cum)和滚动计算(pd.rolling_)。
P a n d a s 累积统计特征函数 \bold{Pandas累积统计特征函数} Pandas累积统计特征函数
方法名 函数功能 所属库 cumsum() 依次给出前1、2、…、n个数的和) Pandas cumprod() 依次给出前1、2、…、n个数的积 Pandas cummax() 依次给出前1、2、…、n个数的max Pandas cummin() 依次给出前1、2、…、n个数的min Pandas rolling_sum() 计算数据样本的总和(按列计算) Pandas rolling_mean() 计算数据样本的算术平均数 Pandas rolling_var() 计算数据样本的方差 Pandas rolling_std() 计算数据样本的标准差 Pandas rolling_corr() 计算数据样本的Spearman (Pearson)相关系数矩阵 Pandas rolling_cov() 计算数据样本的协方差矩阵 Pandas rolling_skew() 样本值的偏度(三阶矩) Pandas rolling_kurt() 样本值的峰度(四阶矩) Pandas 其中,cum系列函数是作为DataFrame或’Series对象的方法而出现的,因此命令格D.cumsum(),而rolling_系列是pandas 的函数,不是DataFrame或Series对象的方法,因此,其中,cum系列函数是作为DataFrame或’Series对象的方法而出现的,因此命令格式为D.cumsum(),而rolling_系列是pandas 的函数,不是DataFrame或Series对象的方法
三、统计作图函数
通过统计作图函数绘制的图表可以直观地反映出数据及统计量的性质及其内在规律,如盒图可以表示多个样本的均值,误差条形图能同时显示下限误差和上限误差,最小二乘拟合曲线图能分析两变量间的关系。
Python的主要作图库是Matplotlib,在第2章中已经进行了初步的介绍,而 Pandas基于Matplotlib并对某些命令进行了简化,因此作图通常是Matplotlib和 Pandas相互结合着使用。本小节仅对一些基本的作图函数做一下简介,而真正灵活地使用应当参考书中所给出的各个作图代码清单。我们要介绍的统计作图函数如表所示。
P y t h o n 主要统计作图函数 \bold{Python主要统计作图函数} Python主要统计作图函数
方法名 函数功能 所属库 plot() 绘制线性二维图,折线图 Pandas/Matplotlib pie() 绘制饼状图 Pandas/Matplotlib hist() 绘制二维条形直方图,可显示数据的分配情形 Pandas/Matplotlib boxplot() 绘制样本数据的箱形图 Pandas plot(logy=True) 绘制y轴的对数图形 Pandas plot(yerr=True) 绘制误差条形图 Pandas 在作图之前,通常要加载以下代码。
import matplotlib.pyplot as plt#导入作图库 plt.rcParams [ 'font.sans-serif'] =[ 'SimHei']#用来正常显示中文标签 plt.rcParams [ 'axes.unicode_minus' ] = False #用来正常显示负号 plt.figure(figsize = (7,5))#创建图像区域,指定比例
作图完成后,一般通过plt.show()来显示作图结果。
3.1 plot()
**功能:**绘制线性二维图、折线图。
使用格式:
p l t . p l o t ( x , y , S ) plt.plot(x,y, S) plt.plot(x,y,S)
这是Matplotlib通用的绘图方式,绘制y对于x (即以x为横轴的二维图形),字符串参量S指定绘制时图形的类型、样式和颜色,常用的选项有: 'b’为蓝色、'r’为红色、'g’为绿色、‘o’为圆圈、’+‘为加号标记、’-‘为实线、’–'为虚线。当x、y均为实数同维向量时,则描出点(x(i),y(i)),然后用直线依次相连。
D . p l o t ( k i n d = ′ b o x ′ ) D.plot(kind = 'box') D.plot(kind=′box′)
这里使用的是 DataFrame x J会数指定作图类型,支持line(线).bar(余形)、barto tL由接数据为纵坐标自动作图,通过kind参数指定作图类型,支持line(线), bar(条形),barh , hist(直方图)、box(箱线图)、kde(密度图)和 area、pie(饼图)等,同时也能够接受plt.plot() 受的参数。因此,如果数据已经被加载为Pandas中的对象,那么以这种方式作图是比较简洁的。
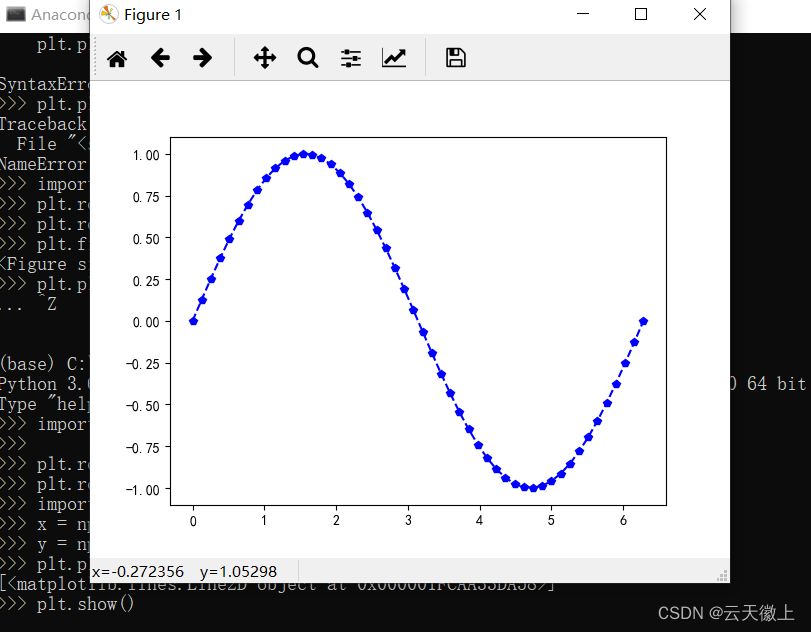
**实例:**在区间(0≤x≤2T)绘制一条蓝色的正弦虚线,并在每个坐标点标上五角星。绘制图形如图所示。
import numpy as np x = np.linspace (0 , 2*np.pi,50)#x坐标输入 y = np.sin (x)#计算对应x的正弦值 plt.plot(x,y, 'bp--')#控制图形格式为蓝色带星虚线,显示正弦曲线 plt.show ( )
3.2 pie()
**功能:**绘制饼型图。
使用格式:
p l t . p i e ( s i z e ) plt.pie(size) plt.pie(size)
使用Matplotlib绘制饼图,其中size是一个列表,记录各个扇形的比例。pie有丰富的参数,详情请参考下面的实例。
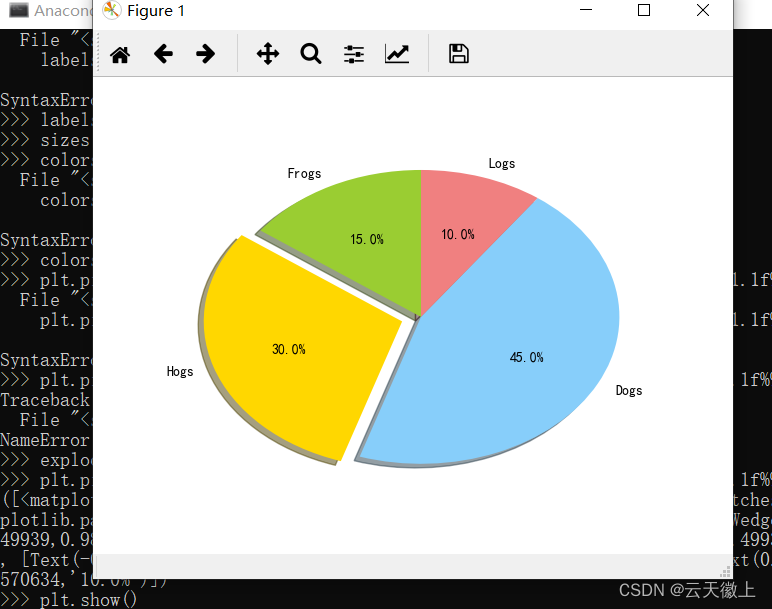
import matplotlib.pyplot as plt # The slices will be ordered and plotted counter-clockwise. labels = 'Frogs ', 'Hogs ', 'Dogs ', 'Logs’#定义标签 sizes =[ 15,30,45,10]#每一块的比例 colors = [ ' yellowgreen', 'gold', 'lightskyblue ', 'lightcoral']#每一块的颜色 explode = (0,0.1,0,0) #突出显示,这里仅仅突出显示第二块(即'Hogs ' ) plt.pie(sizes,explode=explode,labels=labels,colors=colors,autopct='%1.1f%%',shadow=True, startangle=90) plt.axis ( 'equal')#显示为圆(避免比例压缩为椭圆) plt.show ( )
3.3 hist()
**功能:**绘制二维条形直方图,可显示数据的分布情形。
使用格式:
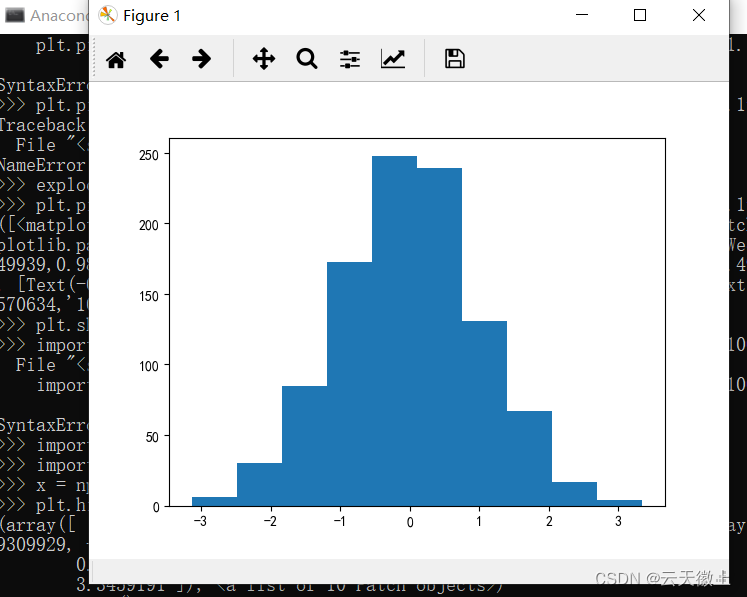
Plt.hist(x, y) 其中,x是待绘制直方图的一维数组,y可以是整数,表示均匀分为n组;也可以是列表,列表各个数字为分组的边界点(即手动指定分界点)。import matplotlib.pyplot as plt import numpy as np x = np.random.randn(1000) plt.hist(x,10) plt.show()
3.4 boxplot()
**功能:**绘制样本数据的箱形图。
使用格式:
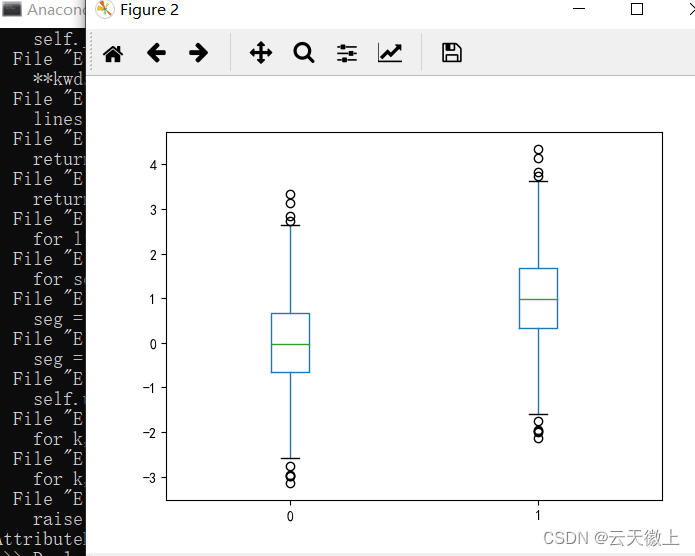
D.boxplot() / D.plot(kind = 'box') 有两种比较简单的方式绘制D的箱形图,其中一种是直接调用DataFrame的 boxplot()方法;另外一种是调用Series或者DataFrame的 plot()方法,并用kind参数指定箱形( box)。其中,盒子的上、下四分位数和中值处有一条线段。箱形末端延伸出去的直线称为表示盒外数据的长度。如果在须外没有数据,则在须的底部有一点,点的颜色与须的颜色相同。 **实例:**绘制样本数据的箱形图,样本由两组正态分布的随机数据组成。其中,一组数据均值为0,标准差为1,另一组数据均值为1,标准差为1。绘制结果如图所示。D = pd.DataFrame([x,x+1]).T D.plot(kind='box') plt.show()
3.5 plot(logx=True)
plot(logx=True)和plot(yerr=error)在数据探索的过程中使用的并不多,这里不做过多的介绍,后续有时间将进行修订。
四、案例研究
在这个案例研究中,我们将使用著名的“泰坦尼克号”数据集,该数据集记录了泰坦尼克号沉船事故中乘客的详细信息,包括他们的生存状况、年龄、性别、舱位等级等。我们的目标是通过数据探索,分析数据质量并提取关键特征,为后续的机器学习模型构建提供有力支持。
数据集介绍:
数据集包含以下字段:PassengerId(乘客ID)、Survived(是否生存)、Pclass(舱位等级)、Name(姓名)、Sex(性别)、Age(年龄)、SibSp(兄弟姐妹/配偶数)、Parch(父母/子女数)、Ticket(船票号)、Fare(票价)、Cabin(船舱号)、Embarked(登船港口)。
数据加载与初步查看:
首先,我们使用Pandas库加载数据并查看前几行以了解数据的大致结构。
import pandas as pd # 加载数据 titanic_data = pd.read_csv('titanic.csv') # 查看数据前5行 print(titanic_data.head())数据质量分析:
接下来,我们进行数据质量分析,重点关注缺失值。
# 检查缺失值 missing_values = titanic_data.isnull().sum() print(missing_values) # 可视化缺失值 import matplotlib.pyplot as plt plt.figure(figsize=(10, 6)) missing_values.plot(kind='bar') plt.title('Missing Values in Titanic Dataset') plt.xlabel('Features') plt.ylabel('Number of Missing Values') plt.show()通过查看缺失值的数量和分布情况,我们发现Age、Cabin和Embarked字段存在缺失值。对于Age,我们可以考虑使用均值、中位数或基于其他特征(如性别和舱位等级)的插值来填充。对于Cabin,由于缺失值太多且可能不包含对预测Survived有用的信息,我们可以考虑删除这个特征。对于Embarked,由于缺失值较少,我们可以考虑使用众数填充。
数据特征分析:
在进行特征分析时,我们关注特征的统计描述、分布以及它们与目标变量Survived的关系。
# 描述性统计 titanic_data.describe() # 查看分类特征的分布 print(titanic_data['Sex'].value_counts()) print(titanic_data['Pclass'].value_counts()) print(titanic_data['Embarked'].value_counts(dropna=False)) # 可视化特征与生存的关系 titanic_data['Survived'].value_counts().plot(kind='bar', label='Survival') plt.title('Survival Counts') plt.xlabel('Survived') plt.ylabel('Count') plt.legend() plt.show() # 以性别为例,查看生存率的差异 gender_survival = titanic_data.groupby('Sex')['Survived'].mean() gender_survival.plot(kind='bar') plt.title('Survival Rate by Gender') plt.xlabel('Gender') plt.ylabel('Survival Rate') plt.show()通过这些分析,我们可以发现性别和舱位等级与生存率有显著的关系。例如,女性乘客的生存率高于男性,高等级舱位的乘客生存率也较高。这些信息对于后续的模型构建和特征选择非常有价值。
数据清洗与特征工程:
基于上述分析,我们进行数据清洗和特征工程。
# 填充Age缺失值,使用中位数填充 titanic_data['Age'].fillna(titanic_data['Age'].median(), inplace=True) # 填充Embarked缺失值,使用众数填充 titanic_data['Embarked'].fillna(titanic_data['Embarked'].mode()[0], inplace=True) # 删除Cabin特征,因为缺失值太多且可能不相关 titanic_data.drop('Cabin', axis=1, inplace=True) # 将分类特征进行编码,例如将Sex编码为数值 titanic_data['Sex'] = titanic_data['Sex'].map({'female': 0, 'male': 1}) titanic_data['Embarked'] = titanic_data['Embarked'].map({'S': 0, 'C': 1, 'Q': 2})特征选择:
在进行了初步的数据清洗和特征工程后,我们可以进一步进行特征选择,以确定哪些特征对预测Survived最为关键。在这个案例中,我们可以通过计算特征与目标变量之间的相关性来进行特征选择。
# 计算特征与生存之间的相关性 correlations = titanic_data.corrwith(titanic_data['Survived']) # 显示相关性 print(correlations) # 基于相关性选择特征 selected_features = correlations[abs(correlations) > 0.1].index titanic_data_selected = titanic_data[selected_features] print(titanic_data_selected.head())
在这个例子中,我们选择了与Survived相关性绝对值大于0.1的特征。这样,我们可以去除那些与目标变量关系不大的特征,减少模型的复杂度,并提高模型的性能。
数据准备与模型训练:
最后,我们将经过清洗、编码和选择后的数据分为训练集和测试集,准备用于机器学习模型的训练。
from sklearn.model_selection import train_test_split # 分离特征和标签 X = titanic_data_selected.drop('Survived', axis=1) y = titanic_data_selected['Survived'] # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 后续可以使用X_train和y_train来训练机器学习模型,并使用X_test和y_test来评估模型的性能。通过本案例研究,我们展示了如何进行数据质量和数据特征分析。首先,我们加载了数据集并检查了缺失值的情况,对缺失值进行了合理的填充或删除。接着,我们对特征进行了描述性统计和可视化分析,了解了特征的分布以及与目标变量的关系。然后,我们进行了特征选择,去除了与目标变量相关性不强的特征。最后,我们准备了数据用于机器学习模型的训练。这个过程是机器学习项目中的重要一环,能够帮助我们更好地理解数据,并为后续的模型构建提供坚实的基础。
小结
本章从应用的角度出发,从数据质量分析和数据特征分析两个方面对数据进行探索分析,最后介绍了Python常用的数据探索函数及用例。数据质量分析要求我们拿到数据后先检测是否存在缺失值和异常值;数据特征分析要求我们在数据挖掘建模前,通过频率分布分析、对比分析、帕累托分析、周期性分析、相关性分析等方法,对采集的样本数据的特征规律进行分析,以了解数据的规律和趋势,为数据挖掘的后续环节提供支持。
要特别说明的是,在数据可视化中,由于主要使用Pandas作为数据探索和分析的工具,因此我们介绍的作图工具都是Matplotlib和Pandas结合使用。一方面,Matplotlib是作图工具的基础,Pandas作图依赖于它;另一方面,Pandas 作图有着简单直接的优势,因此.相互结合,往往能够以最高的效率作出符合我们需要的图。