图【数据结构】

文章目录

• 图的基本概念
• 邻接矩阵
• 邻接表
• 图的遍历
• • BFS
  • DFS

    图的基本概念

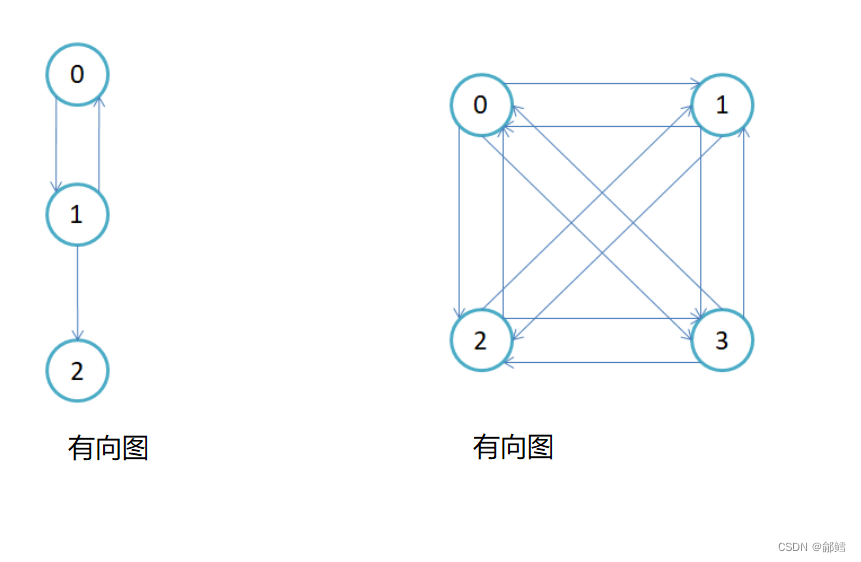
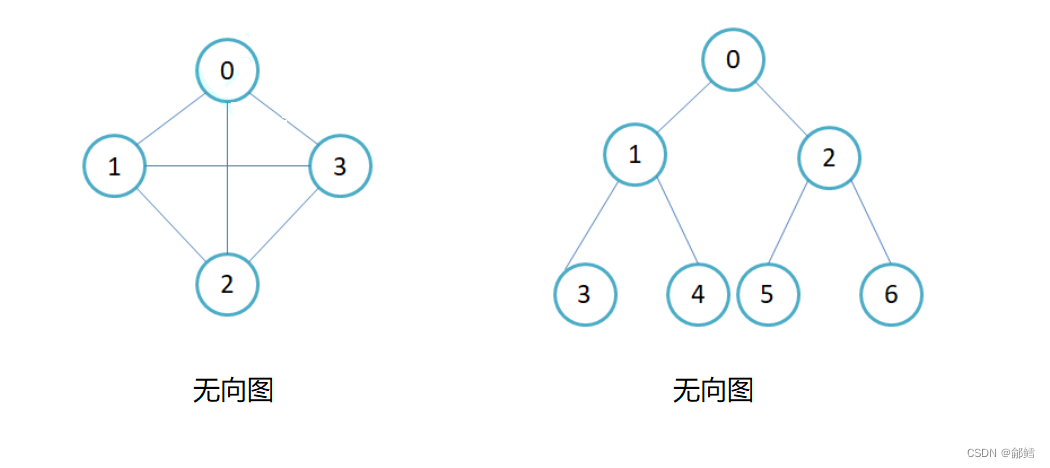
    图是由顶点集合及顶点间的关系组成的一种数据结构

    顶点和边：图中结点称为顶点

    权值:边附带的数据信息

    

    

    路径 ：

    简单路径 和 回路：

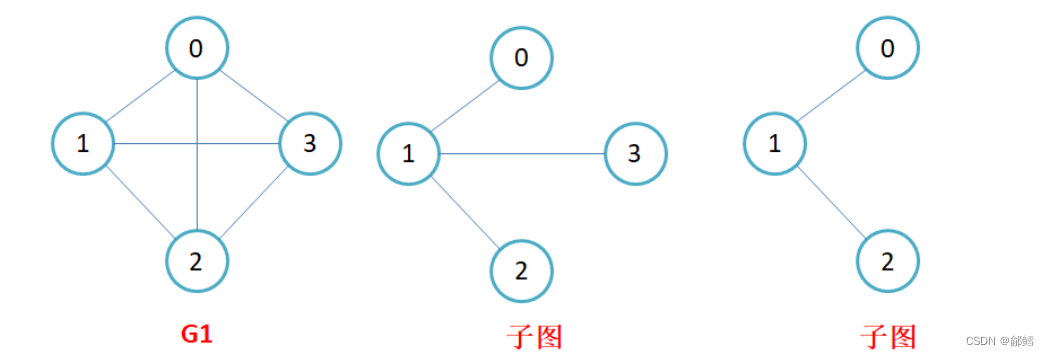
    子图：设图G = {V, E}和图G1 = {V1，E1}，若V1属于V且E1属于E，则称G1是G的子图

    

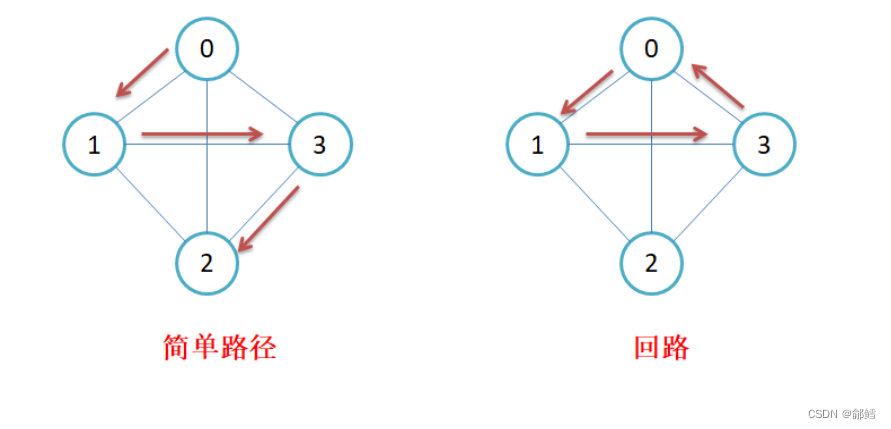
    连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图

    生成树：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边

    生成树就是用最少的边连通起来

    最小生成树:构成生成树这些边加起来权值是最小的。

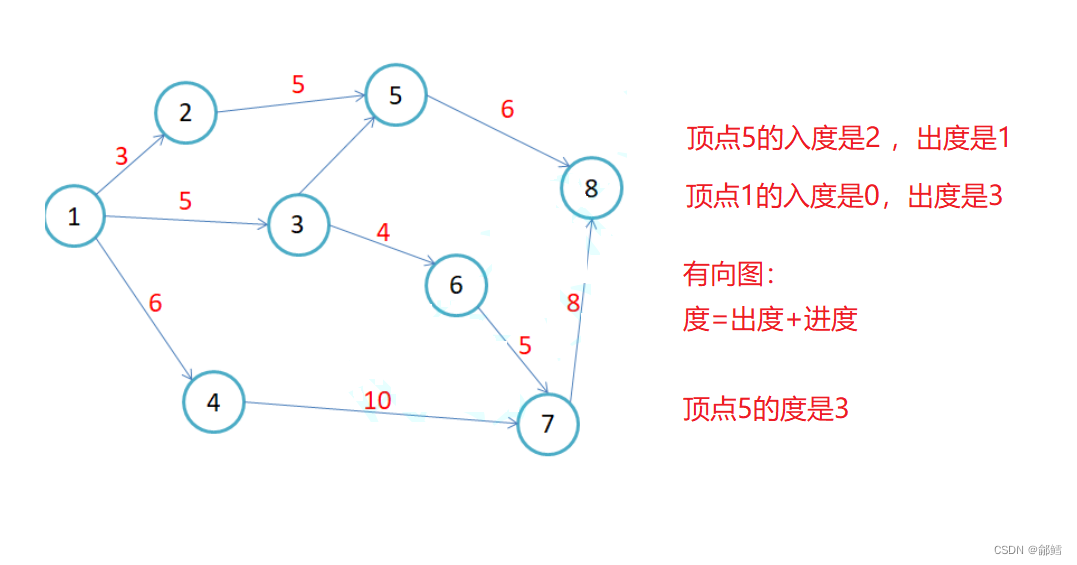
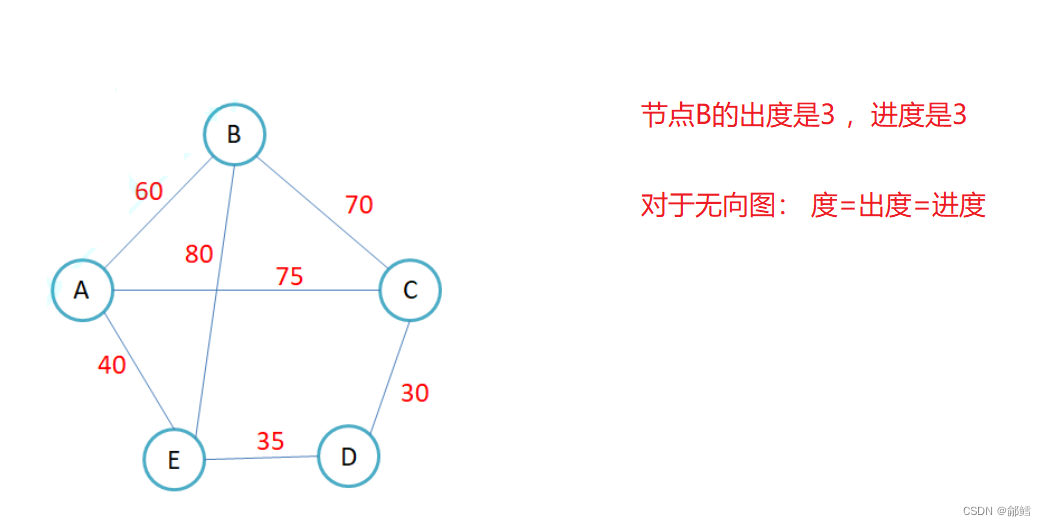
    顶点的度：

    

    

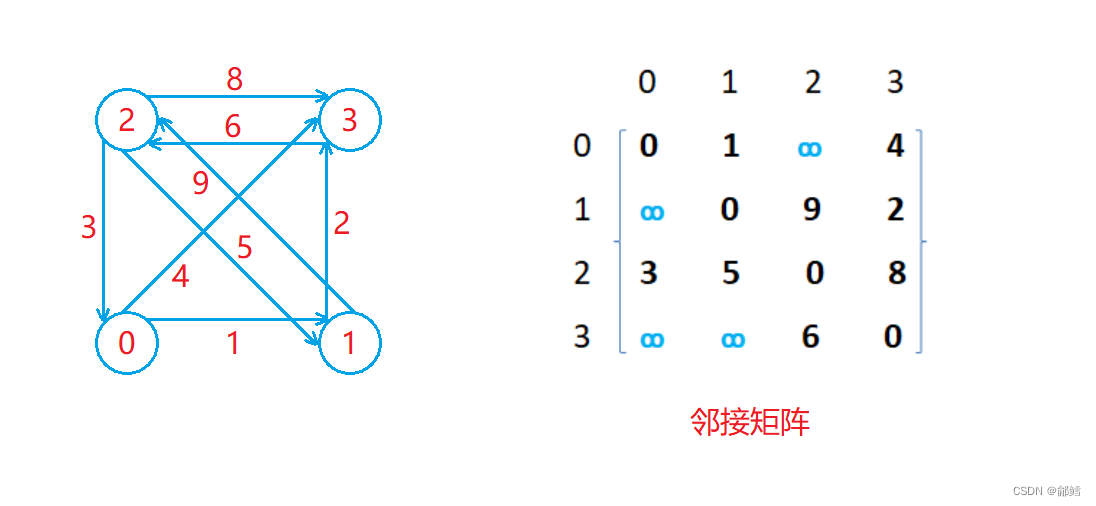
    邻接矩阵

    

    #pragma once 
    #include
    #include
    #include
    #include
    #include
    #include 
    #include
    using namespace std;
    //矩阵 
    namespace matrix
    {
    	//V是顶点 ，W是 weight 权值 
    	template   //true是有向图 ，false是无向图
    	class Graph
    	{
    	public:
    		//手动添加边
    		Graph(const V* a, size_t n)  //用指针数组 存储顶点
    		{
    			_vertex.reserve(n);
    			//初始化顶点和边
    			for (size_t i = 0; i second;
    			}
    			else //没有找到 
    			{
    				assert(false);
    				return -1;
    			}
    		}
    		void AddEdge(const V& src, const V& dst, const W& w)
    		{
    			int srci = GetVertexIndexMap(src);
    			int dsti = GetVertexIndexMap(dst);
    			_matrix[srci][dsti] = w;
    			//无向图 
    			if (Direction == false)
    			{
    				_matrix[srci][dsti] = w;
    				_matrix[dsti][srci] = w;
    			}
    		}
    			void  Print()
    			{
    				//顶点 
    				for (int i = 0; i