数据结构之双向链表详解
😽博主CSDN主页：小源_😽
🖋️个人专栏：《数据结构》🖋️
😀努力追逐大佬们的步伐~
目录
1. 前言
2. LinkedList（无头双向链表）的模拟实现
2.1 定义IList接口
2.2 重写IList中的方法
2.3 display（打印方法）
2.4 size方法
2.5 contains方法
2.6 addFirst头插法
2.7 addLast尾插法
2.8 addIndex任意插法
2.9 remove方法
2.10 removeAllKey方法
2.11 clear方法
3. LinkedList的使用
3.1 什么是LinkedLList
3.2 LinkedList的使用
3.3 LinkedList的遍历
4. 经常遇到的面试问题
1. 前言
上一篇文章中我们重点讲解了无头单向非循环链表的模拟实现，现在我们来讲解LinkedList（无头双向链表实现 ）的模拟实现。
本章重点：
本文着重讲解了LinkedList(无头双向单链表)的实现和LinkedList的使用。
2. LinkedList（无头双向链表）的模拟实现
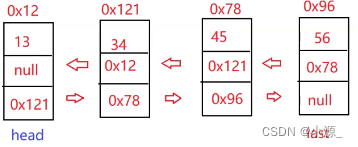
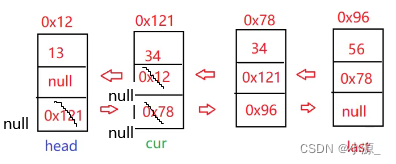
从上图可以看出，无头双向链表和无头单向非循环链表结构类似，只是在每个节点中加入了前一个节点的地址(用prev存储)，使得每个节点可以访问前一个节点。其中第一个节点的前驱prev为空。
2.1 定义IList接口
无头双向链表的模拟实现要定义的接口和上一篇文章中无头单向非循环链表的模拟实现一样，即：
public interface IList {
//头插法
void addFirst(int data);
//尾插法
void addLast(int data);
//任意位置插入,第一个数据节点为0号下标
void addIndex(int index,int data);
//查找是否包含关键字key是否在单链表当中
boolean contains(int key);
//删除第一次出现关键字为key的节点
void remove(int key);
//删除所有值为key的节点
void removeAllKey(int key);
//得到单链表的长度
int size();
//清空
void clear();
//打印
void display();
}
2.2 重写IList中的方法
定义一个MyLinkedList类来实现IList接口，并且重写IList中的方法
（选中IList,快捷键为Ctrl+O）：
首先需要定义一个内部类作为节点的类，用static修饰，代表只能在当前类中使用。
接着定义一个头节点head，尾节点last。
public class MyLinkedList implements IList{
static class ListNode {
public int val;
public ListNode next;
public ListNode prev;
public ListNode(int val) {
this.val = val;
}
}
public ListNode head;
public ListNode last;
@Override
public void addFirst(int data) {
}
@Override
public void addLast(int data) {
}
@Override
public void addIndex(int index, int data) {
}
@Override
public boolean contains(int key) {
return false;
}
@Override
public void remove(int key) {
}
@Override
public void removeAllKey(int key) {
}
@Override
public int size() {
return 0;
}
@Override
public void clear() {
}
@Override
public void display() {
ListNode cur = head;
while (cur != null) {
System.out.println(cur.next + " ");
cur = cur.next;
}
System.out.println();
}
}
2.3 display（打印方法）
遍历双向链表的方法和遍历单链表相同：我们只需关心next域，而不需要关心prev。
@Override
public void display() {
ListNode cur = head;
while (cur != null) {
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();
}
}
2.4 size方法
求链表个数/长度
@Override
public int size() {
ListNode cur = head;
//定义一个计数器
int count = 0;
while (cur != null) {
count++;
cur = cur.next;
}
return count;
}
2.5 contains方法
指的是查找是否包含关键字key是否在单链表当中。这里跟size方法相似，只需遍历链表时判断是否cur.val == key
@Override
public boolean contains(int key) {
ListNode cur = head;
while (cur != null) {
//判断
if (cur.val == key) {
return true;
}
cur = cur.next;
}
return false;
}
2.6 addFirst头插法
指的是将插入的节点存放在链表的第一个位置。
1.实例化一个节点
2.改变插入节点的next和prev
3.改变head
@Override
public void addFirst(int data) {
ListNode node = new ListNode(data);
//如果head为空，则head和last都指向node
if (head == null) {
head = node;
last = node;
} else {
node.next = head;
head.prev = node;
head = node;
}
}
2.7 addLast尾插法
指的是将插入的节点存放在链表的第一个位置。
1.实例化一个节点
2.找到最后一个节点last
3.last.next = node;
node.prev = last;
4.改变last
@Override
public void addLast(int data) {
ListNode node = new ListNode(data);
//如果head为空，则head和last都指向node
if (head == null) {
head = node;
last = node;
} else {
last.next = node;
node.prev = last;
last = node;
}
}
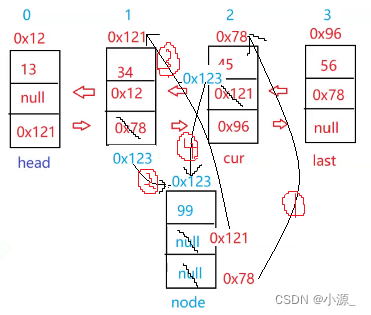
2.8 addIndex任意插法
指的是在任意位置插入一个节点。
1.让cur走index步(单链表的addIndex任意插法为走（index - 1）步)
2.node.next = cur.next;（还是先绑定后面的节点）
cur.prev.next = node;
node.prev = cur.prev;
cur.prev = node;
@Override
public void addIndex(int index, int data) {
int len = size();
//检查index是否合法
if(index len) {
//可以抛出自定义异常
System.out.println("index位置不合法：" + index);
return;
}
if (index == 0) {
addFirst(data);
return;
}
if (index == size()) {
addLast(data);
return;
}
//用cur接收前驱
ListNode cur = findIndex(index);
//实例化一个新的节点
ListNode node = new ListNode(data);
node.next = cur;
cur.prev.next = node;
node.prev = cur.prev;
cur.prev = node;
}
//找到要插入的位置
public ListNode findIndex(int index) {
ListNode cur = head;
while (index != 0) {
cur = cur.next;
index--;
}
return cur;
}
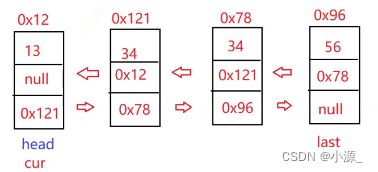
2.9 remove方法
指的是删除第一次出现关键字为key的节点。
1.直接让cur走到index位置
2.删除
@Override
public void remove(int key) {
ListNode cur = head;
while (cur != null) {
if (cur.val == key) {
//删除头节点
if (cur == head) {
head = head.next;
head.prev = null;
} else {
cur.prev.next = cur.next;
//删除最后一个节点
if (cur.next == null) {
last = last.prev;
} else {
cur.next.prev = cur.prev;
}
}
return;
} else {
cur = cur.next;
}
}
}
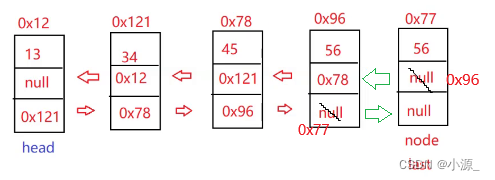
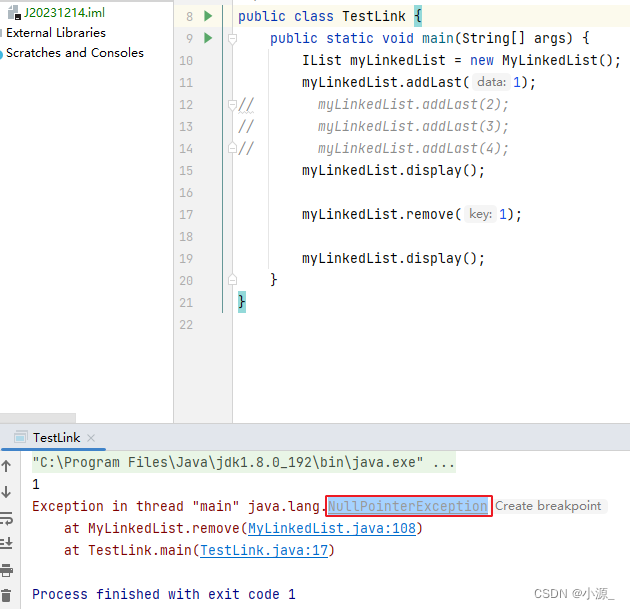
效果图如下：看似很正常，实际上还存在问题 （当节点只有一个时的问题）
如图：第108行代码中，当节点只有一个的情况下，head.next为空,null.prev这一操作会报空指针异常
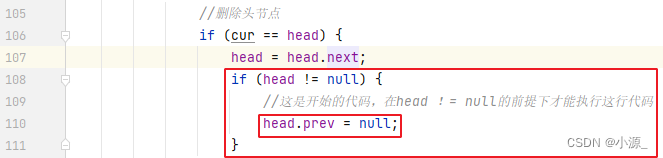
解决方法如下：
效果图如下：此时正常执行
remove方法的最终代码为：
@Override
public void remove(int key) {
ListNode cur = head;
while (cur != null) {
if (cur.val == key) {
//删除头节点
if (cur == head) {
head = head.next;
if (head != null) {
//这是开始的代码，在head ！= null的前提下才能执行这行代码
head.prev = null;
}
last = null;
} else {
cur.prev.next = cur.next;
//删除最后一个节点
if (cur.next == null) {
last = last.prev;
} else {
cur.next.prev = cur.prev;
}
}
return;
} else {
cur = cur.next;
}
}
}
2.10 removeAllKey方法
指的是删除所有值为key的节点。
和remove方法类似，只需把删除操作的一段代码结束以后，不return ,继续cur = cur.next即可
@Override
public void removeAllKey(int key) {
ListNode cur = head;
while (cur != null) {
//删除
if (cur.val == key) {
//删除头节点
if (cur == head) {
head = head.next;
if (head != null) {
//这是开始的代码，在head ！= null的前提下才能执行这行代码
head.prev = null;
}
last = null;
} else {
cur.prev.next = cur.next;
//删除最后一个节点
if (cur.next == null) {
last = last.prev;
} else {
cur.next.prev = cur.prev;
}
}
}
cur = cur.next;
}
}
2.11 clear方法
指的是删除链表的所有节点。
1.直接把头节点和尾巴节点置空的方法太粗糙，我们下面学习更细节的写法：
2.遍历链表，把每个节点的 val = null, prev = null, next = null 即可（val = null可以不写，因为没有人指向这个节点的时候，会被系统自动回收）
@Override
public void clear() {
ListNode cur = head;
while (cur != null) {
//用curNext记录cur.next，因为接下来cur.next将会改变为null
// 我们要用curNext来继续遍历链表
ListNode curNext = cur.next;
cur.val = 0;
cur.next = null;
cur.prev = null;
cur = curNext;
}
head = null;
//暴力做法
// head = null;
// last = null;
}
3. LinkedList的使用
3.1 什么是LinkedLList
LinkedList 的底层是双向链表结构 ，由于链表没有将元素存储在连续的空间中，元素存储在单独的节点中，然后通过引用将节点连接起来了，因此在在任意位置插入或者删除元素时，不需要搬移元素，效率比较高。 在集合框架中， LinkedList 也实现了 List 接口
3.2 LinkedList的使用
1.LinkedList的构造
| 方法 | 解释 |
| LinkedList () | 无参构造 |
| public LinkedList(Collection |
