leetcode刷题（9）二叉树（3）

03-11 1406阅读

各位朋友们，提前祝大家五一劳动节快乐啊！！！今天我为大家分享的是关于leetcode刷题二叉树相关的第三篇我文章，让我们一起来看看吧。

文章目录

1.二叉树的层序遍历

题目要求
做题思路
代码实现
2.从前序与中序遍历序列构造二叉树

题目要求
做题思路
代码实现
3.从中序与后序遍历序列构造二叉树

题目要求
做题思路

代码实现

1.二叉树的层序遍历

leetcode之二叉树的层序遍历（难度：中等）

题目要求

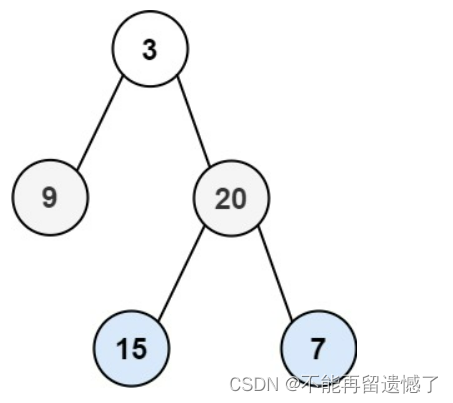
给你二叉树的根节点 root ，返回其节点值的层序遍历。（即逐层地，从左到右访问所有节点）。

示例1

输入：root = [3,9,20,null,null,15,7]

输出：[[3],[9,20],[15,7]]

示例2

输入：root = [1]

输出：[[1]]

示例3

输入：root = []

输出：[]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List levelOrder(TreeNode root) {
    }
}

做题思路

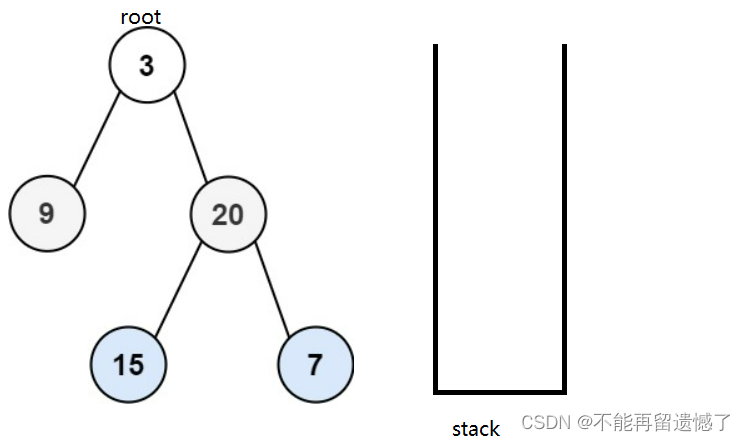
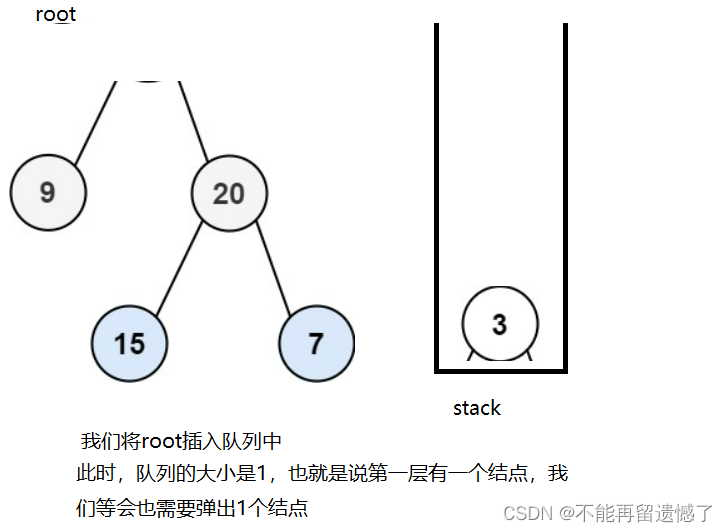
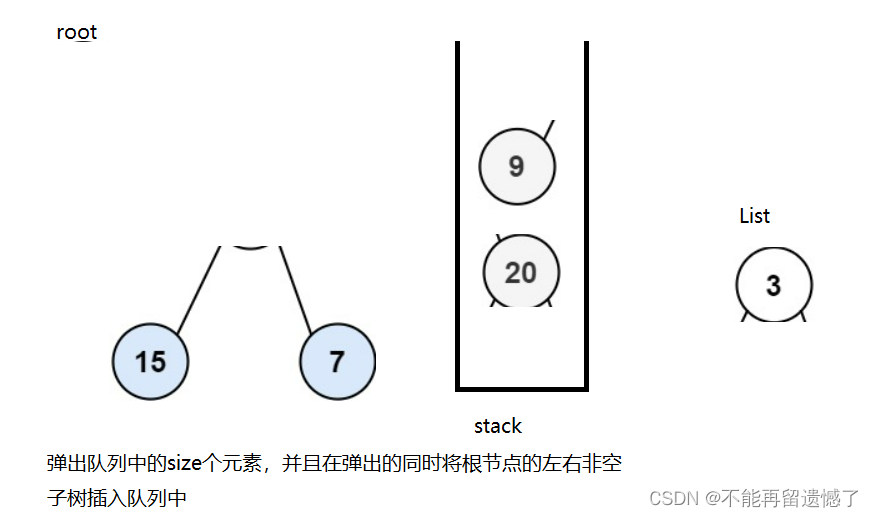
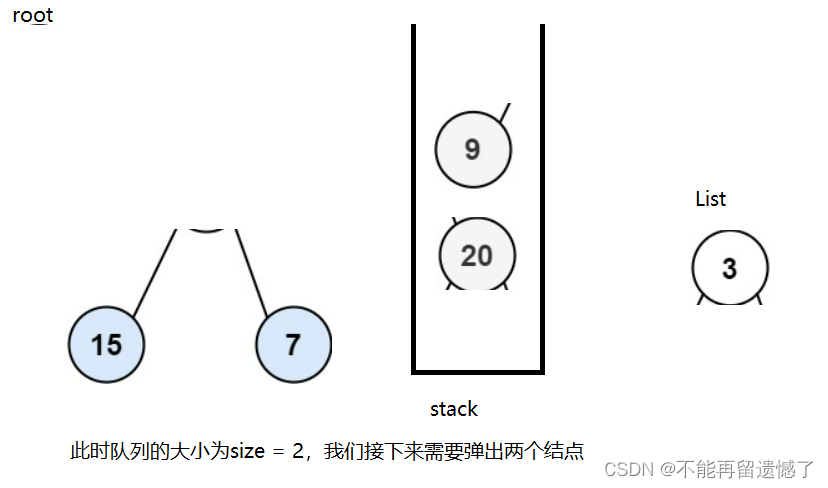
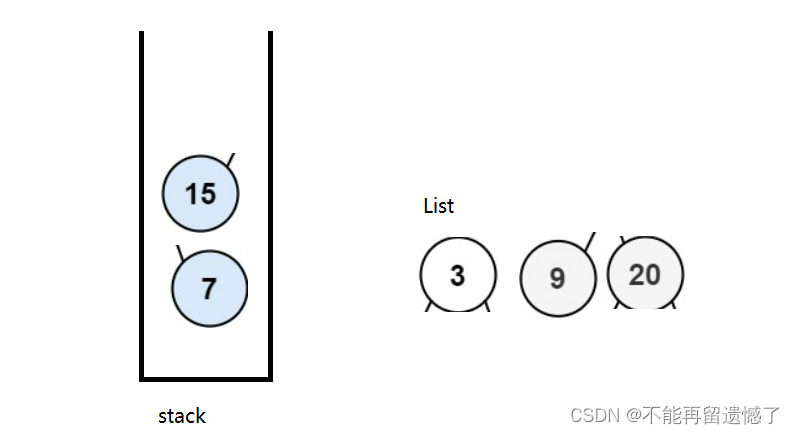
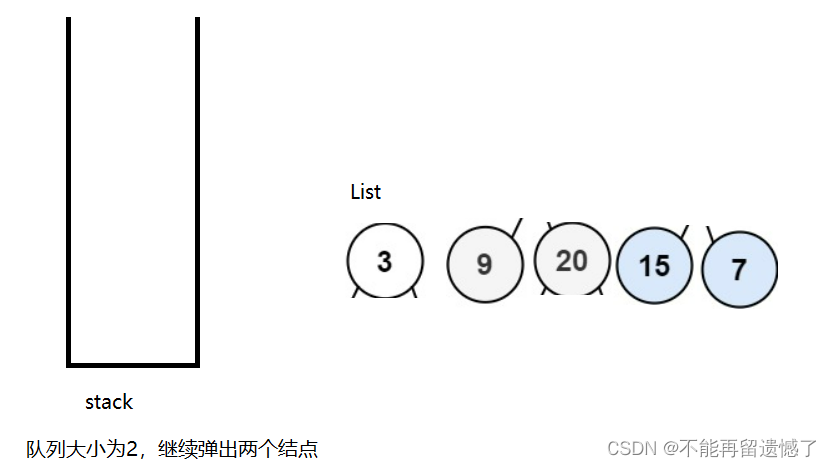
这道题我们可以借助队列这个数据结构，首先先将根节点放进队列中，然后我们计算此时队列的大小，记录下来，这个数字其实就是各层根节点的个数。我们等会要弹出相同数量的元素，在弹出的同时我们需要将弹出的根节点放进List中，并且将次根节点的非空左树和右树插入队列中。我们举个例子。

最后我们返回List就是我们需要的结果。

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List levelOrder(TreeNode root) {
        List list = new ArrayList();
        //当根节点为null时，我们直接返回list，这里list也为null
        if(root == null) {
            return list;
        }
        Queue queue = new LinkedList();
        queue.offer(root);
        while(!queue.isEmpty()) {
            int size = queue.size();
            List tmp = new ArrayList();
            while(size > 0) {
                TreeNode cur = queue.poll();
                tmp.add(cur.val);
                if(cur.left != null) {
                    queue.offer(cur.left);
                }
                if(cur.right != null) {
                    queue.offer(cur.right);
                }
                size--;
            }
            list.add(tmp);
        }
        return list;
    }
}

2.从前序与中序遍历序列构造二叉树

leetcode之从前序与中序遍历序列构造二叉树（难度：中等）

题目要求

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

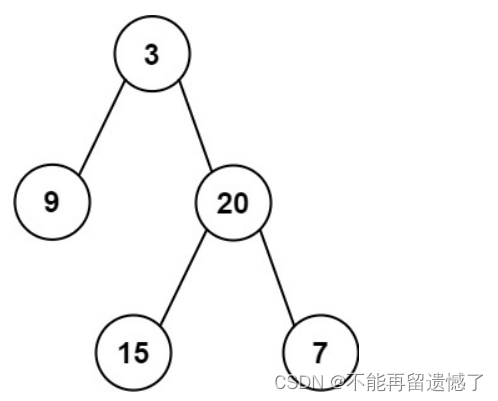
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]

输出: [-1]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
    }
}

做题思路

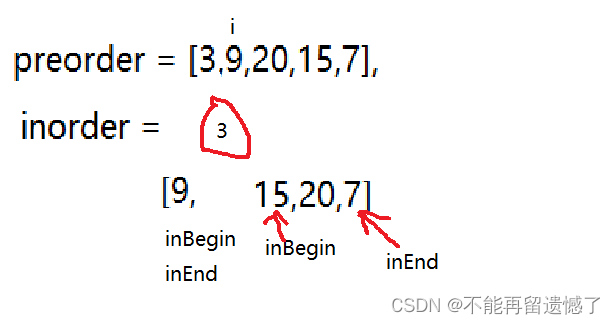
我们通过二叉树的前序遍历序列来确定根节点，通过中序遍历来确定左右子树，我们直接来举一个例子。

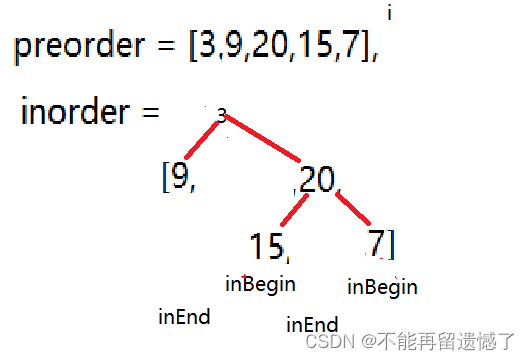
用inBegin和inEnd来分别表示左右子树的范围，当表示左树时inEnd = index-1

表示右树时inBegin = index+1

此时9的左树为null，说明3的左树的树叶是9，也就是说我们递归结束的条件是inBegin > inEnd

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
//创建一个成员变量用来遍历前序遍历序列
    public int i = 0;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
    //我们inBegin默认为0，inEnd默认数组的最后一个元素的下标
        return buildTreeChild(preorder,inorder,0,inorder.length-1);
    }
    public TreeNode buildTreeChild(int[] preorder,int[] inorder,int inBegin, int inEnd) {
    //递归结束的条件
        if(inBegin > inEnd) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[i]);
        int index = findIndex(preorder[i],inorder,inBegin,inEnd);
        i++;
        root.left = buildTreeChild(preorder,inorder,inBegin,index-1);
        root.right = buildTreeChild(preorder,inorder,index+1,inEnd);
        return root;
    }
    public int findIndex(int key,int[] inorder,int inBegin,int inEnd) {
        for(int j = inBegin; j
            if(key == inorder[j]) {
                return j;
            }
        }
        return -1;
    }
}

    public TreeNode buildTree(int[] inorder, int[] postorder) {
    }
}

    public int i = 0;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        i = postorder.length-1;
        return buildTreeChild(inorder,postorder,0,postorder.length-1);
    }
    public TreeNode buildTreeChild(int[] inorder,int[] postorder,int inBegin,int inEnd) {
        if(inBegin  inEnd) {
            return null;
        }
        TreeNode root = new TreeNode(postorder[i]);
        int index = findIndex(postorder[i],inorder,inBegin,inEnd);
        i--;
        root.right = buildTreeChild(inorder,postorder,index+1,inEnd);
        root.left = buildTreeChild(inorder,postorder,inBegin,index-1);
        return root;
    }
    public int findIndex(int key, int[] inorder, int inBegin, int inEnd) {
        for(int j = inBegin; j 
            if(inorder[j] == key) {
                return j;
            }
        }
        return -1;
    }
}

VPS购买请点击我