数据结构：队列

03-01 1216阅读

文章目录

  • 1.队列的概念
  • 2.队列的设计
  • 3.队列的实现
    • 3.1初始化
    • 3.2销毁
    • 3.3入队列
    • 3.4出队列
    • 3.5获取队头元素
    • 3.6获取队尾元素
    • 3.7队中元素个数
    • 3.8检测队是否为空
    • 4.相关题目
      • 4.1用队列实现栈
      • 4.2用栈实现队列

        数据结构：队列

        1.队列的概念

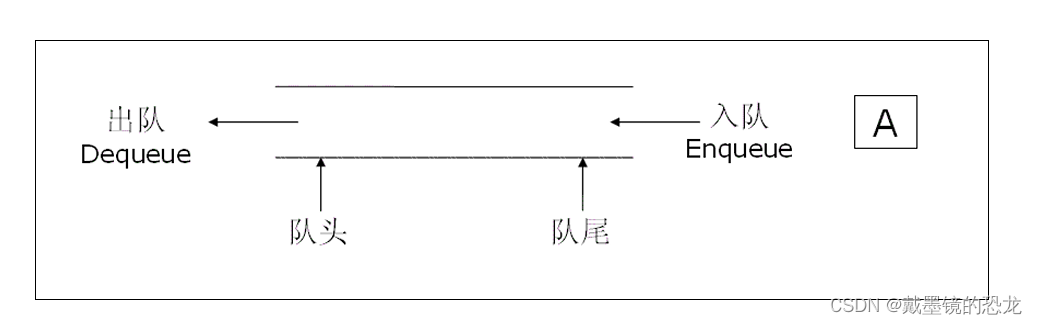
        队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out)

        • 入队列：进行插入操作的一端称为队尾
        • 出队列：进行删除操作的一端称为队头

          数据结构：队列

          2.队列的设计

          1. 队列也可以数组和链表的结构实现，使用链表的结构实现更优一些。因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低，时间复杂度为O(n)。
          2. 若单独使用链表，那在队尾插入数据时，由于需要找队尾，复杂度也为O(n)。所以我们干脆定义两个指针，指针指向链表的头尾，在对队列进行操作时，仅操作这两个指针即可。
          //链表的节点
typedef int QueueDataType;
typedef struct QueueNode
{
	QueueDataType data;
	struct QueueNode* next;
}QNode;
//队列
typedef struct Queue
{
	QNode* head;//指向队头的指针
	QNode* tail;//指向队尾的指针
	int size; //记录当前队中元素的个数
}Queue;

          3.队列的实现

          3.1初始化

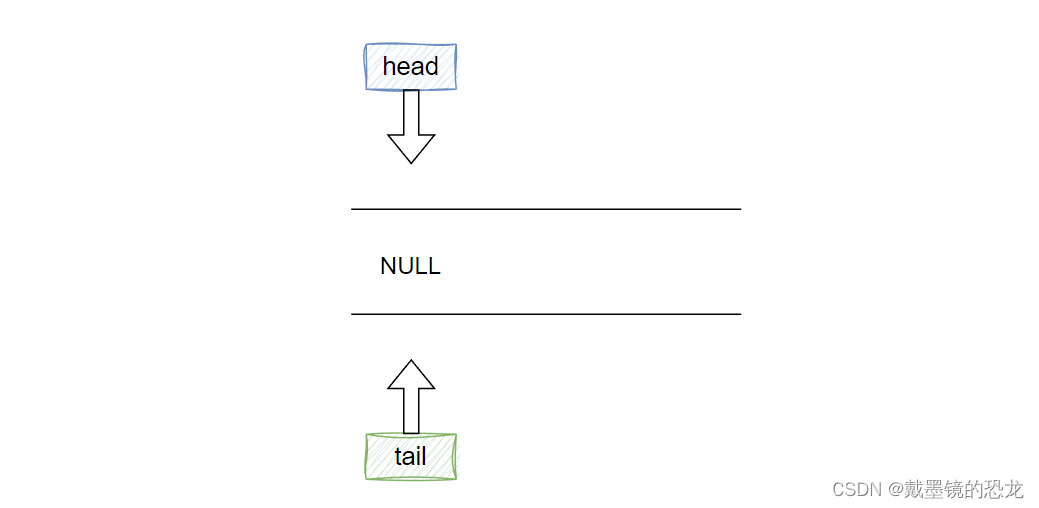
          最开始时，队头指针与队尾指针均指向空，队列中没有元素。

          //初始化
void QueueInit(Queue* q)
{
	assert(q);
	q->head = NULL;
	q->tail = NULL;
	q->size = 0;
}

          数据结构：队列

          3.2销毁

          //销毁
void QueueDestroy(Queue* q)
{
	assert(q);
	QNode* cur = q->head; //cur应该为节点类型，而不是队列
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	q->head = NULL;
	q->tail = NULL;
	q->size = 0;
}

          3.3入队列

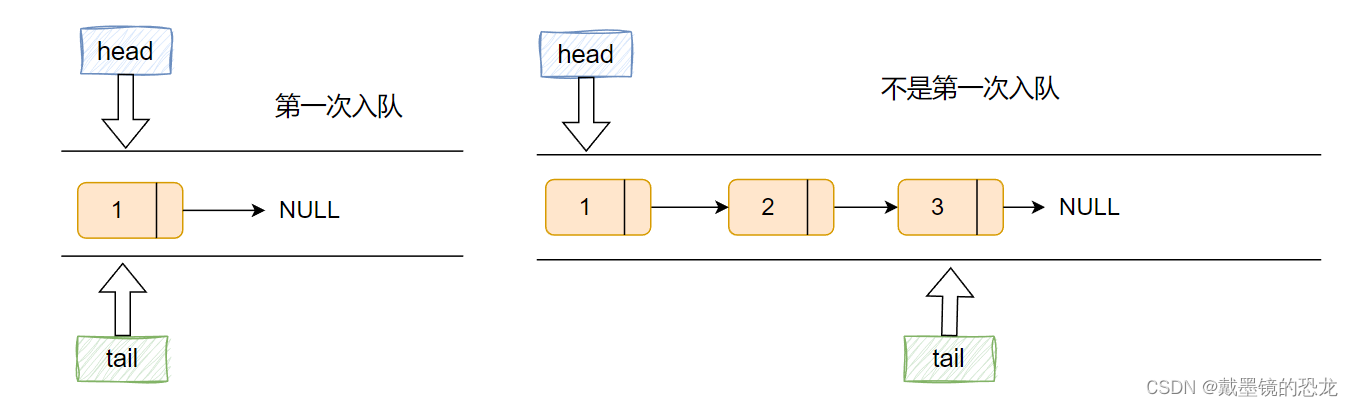
          入队列非常简单，只需向队尾后插入数据，然后队尾后移，队列元素个数加一。

          • 若是第一次入队，队尾与队头均指向入队节点
          • 不是第一次入队，直接向队尾插入

            数据结构：队列

            //入队列
void QueuePush(Queue* q, QNodeDataType x)
{
	assert(q);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return;
	}
	newnode->data = x;
	newnode->next = NULL;
	//若是第一次入队
	if (q->head == NULL)
	{
		q->head = q->tail = newnode;
	}
	else
	{
		//不是第一次
		q->tail->next = newnode;
		q->tail = q->tail->next;
	}
	q->size++;//队列元素个数加一
}

            3.4出队列

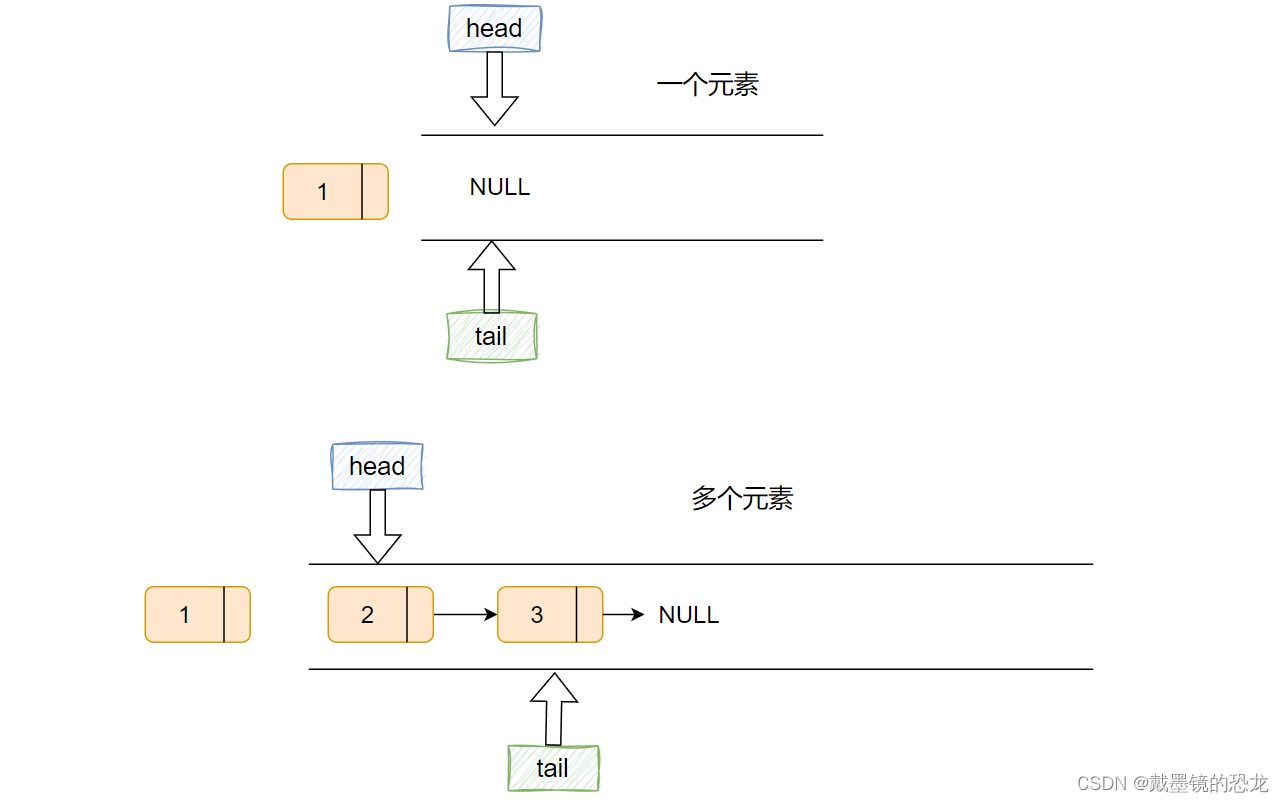
            出队列有几个需要注意的地方：

            • 队列不能为空
            • 只有一个元素时，队头元素出队列后，队头、队尾指针置空
            • 多个元素，队头元素出队列后，队头后移

              数据结构：队列

              //出队列
void QueuePop(Queue* q)
{
	assert(q);
	assert(q->head);//队不能为空
	//只有一个节点
	if (q->head->next == NULL)
	{
		free(q->head);
		q->head = q->tail = NULL;
	}
	else
	{
		//多个节点
		QNode* next = q->head->next;
		free(q->head);
		q->head = next;
	}
	q->size--;
}

              3.5获取队头元素

              //获取队头元素
QNodeDataType QueueFront(Queue* q)
{
	assert(q);
	assert(q->head);//队列不为空
	return q->head->data;
}

              3.6获取队尾元素

              QNodeDataType QueueBack(Queue* q)
{
	assert(q);
	assert(q->tail);
	return  q->tail->data;
}

              3.7队中元素个数

              //队中元素个数
int QueueSize(Queue* q)
{
	assert(q);
	return q->size;
}

              3.8检测队是否为空

              //队是否为空
bool QueueEmpty(Queue* q)
{
	assert(q);
	return q->size == 0;
}

              4.相关题目

              4.1用队列实现栈

              数据结构：队列

              本题的解题思路是这样的：

              • 让一个队列为空，一个队列存数据
              • 入栈时，向不为空的队列中入数据
              • 出栈时
                • 将不为空队列中的n-1个数据入到另一个为空的队列中
                • 然后再将该队列第n个数据出队

                  这样我们就利用两个队列来回的导数据实现了栈的效果。

                  typedef struct {
    Queue q1;
    Queue q2;
} MyStack;
MyStack* myStackCreate() {
    MyStack* ps = (MyStack*)malloc(sizeof(MyStack));
    QueueInit(&ps->q1);
    QueueInit(&ps->q2);
    return ps;
}
void myStackPush(MyStack* obj, int x) {
    //哪个不为空就往哪个里面入
    if(QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q2,x);
    }
    else
    {
        QueuePush(&obj->q1,x);
    }
}
int myStackPop(MyStack* obj) {
    
    Queue* emptyQueue = &obj->q1;
    Queue* NonEmptyQueue = &obj->q2;
    if(!QueueEmpty(&obj->q1))
    {
        NonEmptyQueue = &obj->q1;
        emptyQueue = &obj->q2;
    }
    //将n-1个到入空队列
    while(QueueSize(NonEmptyQueue) > 1)
    {
        //非空队列出
        QNodeDataType front = QueueFront(NonEmptyQueue);
        QueuePop(NonEmptyQueue);
        //向空队列中入
        QueuePush(emptyQueue,front);
    }
    //第n个数据出队列(出栈)
    int front = QueueFront(NonEmptyQueue);
    QueuePop(NonEmptyQueue);
    return front;
}
//取栈顶数据==取队尾数据
int myStackTop(MyStack* obj) {
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}
//两个队列都为空，栈才为空
bool myStackEmpty(MyStack* obj) {
    
    return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}
void myStackFree(MyStack* obj) {
    
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

                  4.2用栈实现队列

                  数据结构：队列

                  解题思路：

                  将一个栈当作输入栈，用于压入传入的数据；另一个栈当作输出栈，用于pop 和 peek 操作。

                  每次 pop 或 peek时，只有输出栈为空才将输入栈的全部数据依次弹出并压入输出栈，这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。

                  typedef struct {
    Stack input;
    Stack output;
} MyQueue;
MyQueue* myQueueCreate() {
    MyQueue* pq = (MyQueue*)malloc(sizeof(MyQueue));
    StackInit(&pq->input);
    StackInit(&pq->output);
    return pq;
}
void myQueuePush(MyQueue* obj, int x) {
    StackPush(&obj->input,x);
}
int myQueuePop(MyQueue* obj) {
    
    //输出栈为空，倒数据
    if(StackEmpty(&obj->output))
    {
        while(!StackEmpty(&obj->input))
        {
            int top = StackTop(&obj->input);
            StackPop(&obj->input);
            StackPush(&obj->output,top);
        }
    }
    //输出栈不为空，直接出栈顶数据
    int front = StackTop(&obj->output);
    StackPop(&obj->output);
    return front;
}
int myQueuePeek(MyQueue* obj) {
    //输出栈为空，倒数据
    if(StackEmpty(&obj->output))
    {
        while(!StackEmpty(&obj->input))
        {
            int top = StackTop(&obj->input);
            StackPop(&obj->input);
            StackPush(&obj->output,top);
        }
    }
    return StackTop(&obj->output);
}
bool myQueueEmpty(MyQueue* obj) {
    return StackEmpty(&obj->input) && StackEmpty(&obj->output);
}
void myQueueFree(MyQueue* obj) {
    
    StackDestroy(&obj->input);
    StackDestroy(&obj->output);
    free(obj);
}
VPS购买请点击我

文章版权声明：除非注明，否则均为主机测评原创文章，转载或复制请以超链接形式并注明出处。

相关阅读

目录[+]